Основні статистичні характеристики випадкової вибірки

Характеристики	Оцінки вибіркових значень
1	2
1. Середні значення:
арифметичне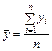
геометричне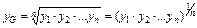
гармонійне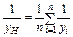
2. Дисперсія	(незміщена оцінка)
Середньоквадратичне відхилення (СКВ)
3. Середнє абсолютне лінійне відхилення
4. Початкові моменти: дру­гого, третього, четвертого порядку	; ;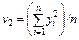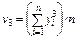
5. Моменти центральні:
другого,	;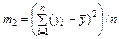
третього,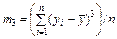
четвертого порядку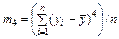
9. Коефіцієнт асиметрії
його незміщена оцінка
СКВ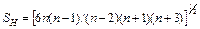
10. Показник ексцесу
його незміщена оцінка
СКВ
11. Коефіцієнти варіації:
за розмахом
за середнім абсолютним лі­нійним відхиленням
за СКВ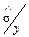
медіана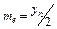
мода	— характеризує величину, яка найчастіше спостерігається
мінімальне значення ряду	y min
максимальне значення ряду	y max
розмах	R= y max – y min

Метод Ірвіна ґрунтується на порівнянні сусідніх значень ряду та розрахунку характеристики , яка дорівнює:

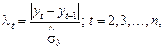; (1.1.15)

де 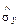— оцінка середньоквадратичного відхилення вибіркового ряду 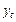, яка розраховується з використанням формул:

, .

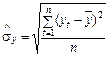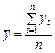Розрахункові значення , тощо порівнюють із критичним значенням , і якщо вони не перевищують критичне, то відповідні рівні 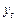вважаються нормальними. Критичні значення для рівня значущості α = 0,05 (помилка 5 %) наведено в табл. 1.1.6.

Таблиця 1.1.6

п
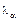
	2,8	2,3	1,6	1,3	1,2	1,1	1,0

Критерій Ірвіна не «сприймає» аномальність, якщо вона виявляється в середині ряду зі стрімкою динамікою, тобто коли стрибок великий, але не перевищує рівнів наприкінці періоду спостережень, оскільки величина характеризує відхилення значень показника від середнього рівня за всією сукупністю спостережень.

Модифікація цього методу пов’язана із послідовним розрахун­ком не за всією сукупністю, а за трьома спостереженнями. Так, для всіх або лише для підозрюваних в аномальності рівнів розраховують оцінки середнього і середньоквадратичного відхилення для двох сусідніх із ними значень:

(1.1.16)

. (1.1.17)

Обчислюють величину , t = 2, 3,…, n. (1.1.18)

Розраховані ковзні значення порівнюють із критичними значеннями (див. табл. 1.1.6.) для .

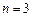Викривлення тенденції свідчить про зміну закономірності розвитку процесу або про зміну методики обчислення значень показника. Якщо точно встановлено, що причиною аномальності є помилки першого роду, то аномальні спостереження замінюють або простою середньою арифметичною двох сусідніх рів­нів ряду, або відповідними значеннями за кривою, що згладжує цей часовий ряд. Не перевіряють часові ряди з періодом сезонності, більшим за одиницю, а також кінцеві рівні періоду спостережень.

Якщо значення наприкінці часового ряду «випадає» із загальної тенденції, то без додаткової інформації стосовно причин «випадіння» в кінці ряду неможливо визначити, чи це спостереження аномальне, чи відбувається зміна тенденції. У цьому разі важливо провести якісний аналіз змін, що відбуваються, або дочекатися надходження результатів нового спостереження. Якщо викривлення тенденції пояснюється зміною методики обчислення показ­ника, то рівні, що передують викривленню тенденції, можуть бути використані для оцінювання характеристик динаміки і побудо­ви моделі за умови, що вони будуть обчислені за новою методикою. Якщо таке обчислення неможливе, ці рівні ряду треба виключити з розгляду. Якщо викривлення тенденції відображає зміну закономірності розвитку процесу, то за інформаційну базу для статистичного аналізу можна взяти лише значення, що відповідають останнім змінам.

Стійкість часового ряду відбиває перевагу закономірності над випадковістю у зміні рівнів ряду. На графіках стійких часових рядів унаочнюється закономірність, а на графіках несталих рядів зміни послідовних рівнів постають хаотичними, тож пошук закономірностей формування значень рівнів таких рядів марний.

Достатня сукупність спостережень насамперед характеризує повноту даних. Достатня кількість спостережень визначається залежно від мети дослідження динаміки. Якщо метою є описовий статистичний аналіз, то період дослідження можна обрати будь-який, на власний розсуд. Якщо мета дослідження — побудова прогнозної моделі, тоді для статистичного аналізу, який розглядає незалежні спостереження з однаковим розподілом, кількість рівнів динамічного ряду має бути якомога більшою і, як правило, не менш як утричі має перевищувати період упередження прогнозу й становити більше 7. У разі використання квартальних або місячних даних для дослідження сезонності й прогнозування сезонних процесів часовий ряд має містити квартальні або місячні дані не менш як за чотири роки, навіть якщо складають прогноз на 1—2 квартали (місяці).

У методах нелінійної динаміки підхід до формування достатньої кількості даних відрізняється від прийнятого більшістю статистиків. У стандартній статистичній теорії чим більше даних точок спостережень, тим краще, бо спостереження перед­бачаються як незалежні. Нелінійні динамічні системи характеризуються процесами із довготривалою пам’яттю. Тому для них охоплення більшого періоду часу є важливішим, ніж збільшення кількості точок спостережень. Наприклад, щоденна вибірка за чотири роки, або 1040 спостережень, не дадуть такого результату, як щомісячні дані за сорок років, або загалом 480 спостережень. Причина полягає в тому, що щоденні дані утворюють лише один чотирирічний цикл, а щомісячні — десять циклів. Нелінійні процеси мають так звану «стрілу часу». Збільшення «частоти» даних часто навіть ускладнює аналіз і не поліпшує значущості результату.

Дата добавления: 2014-11-08