Модель Солоу. Трисекторна модель економічного зростання

Ø Модель Солоу також є односекторною моделлюекономічного зростання. Економічна система розглядається як єдине ціле, що виробляє один універсальний продукт, який можна споживати й інвестувати. Модель доволі адекватно відображає найважливіші макрекономічні аспекти процесу відтворення. Експорт — імпорт у явному вигляді в ній не враховано.

Стан економіки в моделі Солоу визначають такі п’ять ендогенних змінних:

X — валовий внутрішній продукт (ВВП);

С — фонд невиробничого споживання;

І — інвестиції;

L — кількість зайнятих;

К — фонди.

Окрім того, в моделі використовують такі екзогенні показники (задані поза системою):

ν — річний темп приросту кількості зайнятих;

μ — частка основних виробничих фондів, що вибули за рік;

ρ — частка нагромадження (частка валових інвестицій у валовому внутрішньому продукті).

Екзогенні параметри перебувають у таких межах: –1 < ν < 1, 0 < μ< 1, 0 < ρ < 1.

Припускається, що ендогенні змінні змінюються з часом (аргумент t пропущено, але він присутній за визначенням). Екзогенні показники вважаються постійними у часі, причому норма нагромадження є параметром управління, тобто в початковий момент часу може встановлюватися керівним органом системи з огляду на будь-яке гранично допустиме значення.

Час t вважається безперервним і вимірюється у роках. Для миттєвих значень показників L = L (t), К = K (t)в будь-який день можна з’ясувати кількість зайнятих і — шляхом інвентаризації — обсяг основних виробничих фондів. Значення показників типу потоків X = X (t), I = I (t), С = C (t)у момент t = [ t ] + { t } визначають у вигляді нагромаджених за рік, що починається на { t }днів пізніше 1 січня року [ t ].

Припускають, що річний випуск у кожен момент часу визначається лінійно-однорідною неокласичною виробничою функцією

X = F (K, L). (2.1.21)

Згідно з визначенням темпу приросту

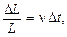або ,

тому

InL = ν t + lnA, L = Ae ^{ν t} .

Використовуючи початкову умову L (0)= L ₀, одержуємо L = L ₀ e ^{ν t} .

Зношування та інвестиції в розрахунку на рік дорівнюють μ K та I відповідно, а за час Δ t — становить відповідно μ K Δ t, I Δ t, тому приріст фондів за цей час дорівнюватиме Δ К = – μ K Δ t + I Δ t, звідки маємо диференціальне рівняння:

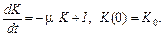
Інвестиції та фонд споживання виражають через ВВП таким чином:

І = ρ Х, С = (1 – ρ) Х.

Отже, маємо такий запис моделі Солоу в абсолютних показниках:

L = L ₀ e ^{ν t} ; ;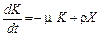

K (0) = K ₀; Х = F (K, L); І = ρ Х; С = (1 – ρ) Х. (2.1.22)

Оскільки

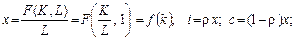
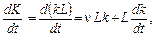
то запис моделі в питомій вазі показників набуває форми:

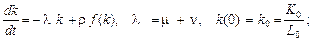
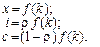(2.1.23)

Отже, кожен абсолютний або відносний показник змінюється в часі, тобто можна говорити про траєкторію системи в абсолютних або відносних показниках.

Траєкторію називають стаціонарною, якщо показники з часом не змінюються:

k = k ⁰ = const, х = х ⁰= const, I = I ⁰ = const, с = с ⁰ = const.

Як видно з формул (2.1.23), перебування фондоозброєності на постійному рівні k^E приводить до виходу на стаціонарну траєкторію. На стаціонарній траєкторії 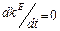, тому

,

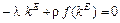або (2.1.24)

.

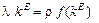Якщо k ⁰ = k^E,то економіка, яка вже перебуває на стаціонарній траєкторії, може зійти з неї лише в разі зміни зовнішніх умов (встановлення іншого значення норми нагромадження, перехід до нових технологій зі зміною функції F (K, L)).

За k ⁰ ≠ k^E в економіці відбуватиметься перехідний процес, який завершиться встановленням стаціонарного режиму. У перехідному режимі фондоозброєність задовольняє рівнянню:

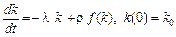, (2.1.25)

причому за та .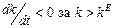

Диференціюванням (2.1.25) знаходимо

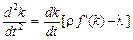, (2.1.26)

звідки видно, що

а) за 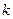< 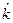маємо ,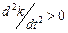

б) за , навпаки, ,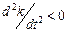

в) за k > k^E завжди 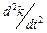> 0, оскільки 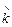< k^E.

Розглянемо перехідний процес для випадку, коли виробничу функ­цію описано функцією Кобба-Дугласа (2.1.7) .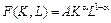

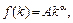
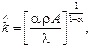
Тоді , а рівняння (2.1.25) набуває вигляду

(2.1.27)

Зробивши заміну 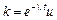, ,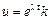одержимо для и рівняння із розділеними змінними:

яке має такий розв’язок: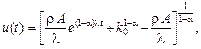

а з використанням значення стаціонарної фондоозброєності запишеться як:

u (t) = [(k^E)^1-α e ^{(1-α) λt} + (k ₀)^1-α – (k^E)^1-α]^1/1-α.

Повертаючись до фондоозброєності, отримаємо

K (t) = [(k^E)^1-α + ((k ₀)^1-α – (k^E)^1-α) e ^(1-α)λt]^1/1-α,

звідки видно, що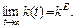

Відповідно до (2.1.26) отримуємо три типи перехідного процесу стосовно фондоозброєності:

1) за 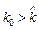— спочатку відбувається пришвидшене зростання фондоозброєності, яке після досягнення значення k переходить на повільне зростання;

2) за 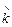< k ₀< k^E спостерігаємовповільнене зростання фондо-
озброєності;

3) за k ₀ > k^E — уповільнений спад фондоозброєності («проїдання» фондів).

Таким чином, за 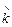< k ₀ < k^E існує зовсім короткий перехідний процес.

У реальній економіці освоєння капітальних вкладень відбувається із запізненням, тобто інвестиції перетворюються на фонди не миттєво, а впродовж певного часу.

Існують два підходи до моделювання запізнень. Перший полягає в тому, що запізнення відбувається із фіксованим лагом τ,тим самим введення фондів у момент t V (t)є просто інвестиціями, зробленими в момент t – τ, тобто

V (t) = I (t – τ). (2.1.28)

Другий підхід полягає у використанні розподіленого лага. При цьому передбачають, що інвестиції, зроблені в момент τобсягом I (τ), на далі освоюватимуть поступово, частками, згідно з певним розподілом N (t, τ) > 0, причому 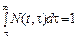. Оскільки інвестиції здійснюються не лише в якийсь фіксований момент часу, а взагалі в будь-який момент τ, то до часу t накопичується обсяг фондів, які підлягають введенню, а саме:

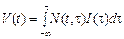. (2.1.29)

Якщо процес інвестування та введення в дію має стаціонарний характер, тоді N (t, τ) = N (t – τ). Отже, (2.1.29) можна переписати таким чином:

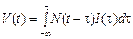. (2.1.30)

Далі приймаємо, що розподіл N (t – τ) є показниковим:

,

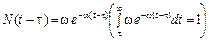тому

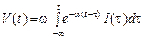. (2.1.31)

У результаті прямого диференціювання (2.1.31) маємо

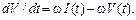(2.1.32)

Додаючи останнє рівняння до відповідним чином скоригованої системи рівнянь стандартної моделі Солоу, одержуємо односекторну модель економікиз урахуванням затримки введення фондів:

Х = I+ С;

X = F (K, L);

dK/dt = – μ K + V, K (0) = K ₀;(2.1.33)

dV/dt = ω I – ω V;

L = L ₀ e ^{ν t} .

Перше рівняння (2.1.33) — баланс розподілу ВВП на інвестиції та невиробниче споживання; друге — виробнича функція валового внутрішнього продукту залежно від ресурсів; третє — динаміка фондів залежно від зношування й уведення фондів; четверте — динаміка введення фондів із урахуванням інвестицій і затримки введення фондів; п’яте — динаміка трудових ресурсів.

Якщо, подібно до попередніх параграфів, вважати, що виробнича функція є лінійно-однорідною неокласичною, то рівняння (2.1.33) можна представити так: (i = I/L, c= C/L, f = F/L,ν = V/L):

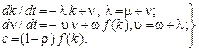(2.1.34)

Стаціонарна точка диференціальних рівнянь (2.1.34) задається такими алгебраїчними рівняннями:

. (2.1.35)

Розв’язавши цю систему рівнянь відносно ν ^E,отримаємо рівняння для k^E,

– λυ k^E + ωρ f (k^E) = 0. (2.1.36)

Якщо f″ (0) = ∞, f (k) > 0, f″ (k) < 0,то (2.1.36) має один розв’язок (виключаючи тривіальний k^E = 0).

Ø Трисекторна модель економічного зростання [34]. Економіку в моделі розподіляють на три сектори: матеріальний (нульовий) — виробляє предмети праці; фондоутворювальний (перший) — вироб­ництво засобів праці; споживчий (другий) сектор — виробництво предметів споживання.

Припускають, що за кожним сектором закріплено основні виробничі фонди (ОВФ), тоді як праця й інвестиції можуть вільно пересуватися між секторами.

Окрім того, застосовують припущення, аналогічні до зроблених в односекторній моделі Солоу, яка відіграє роль базової.

1. Технологічний устрій вважається сталим і визначається
за допомогою лінійно-однорідних неокласичних виробничих функцій

X_i = F_i (K_i, L_i,) i = 0, 1, 2,

де X_i, K_i, L_i — відповідно випуск, ОВФ і кількість зайнятих у i -му секторі.

2. Загальна кількість зайнятих L (у виробничій сфері) змінюється із постійним темпом приросту ν.

3. Лаг капіталовкладень відсутній.

4. Коефіцієнти зношування ОВФ μ _i і прямих матеріальних витрат а_i секторів постійні.

5. Економіка закрита, тобто зовнішня торгівля безпосередньо не розглядається.

6. Час t змінюється неперервно.

Припущення (2) в дискретному часі має вигляд (t — номер року):

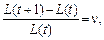
у разі переходу до неперервного часу набуває форми диференціального рівняння:

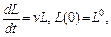
яке має такий розв’язок:

(2.1.37)

Із припущень (3, 4) виходить, що зміна за рік ОВФ i -го сектора складається з двох частин: зносу (– μ _iK_i) та приросту за рахунок валових капіталовкладень (+ І_і), тобто:

K_i(t + 1) – K_i(t) = – μ_iK_i(t) + І_і(t), i = 0, 1, 2,

або в неперервному часі:

K_i(t + Δt) – K_i(t) = – [μ_iK_i(t) + І_і(t)]Δt,

за Δ t → 0 одержуємо диференціальні рівняння для ОВФ секторів:

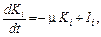
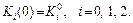(2.1.38)

Далі індекс часу t скрізь пропущено, але передбачається за визначенням. ОВФ і кількість зайнятих у секторах (K_i, L_i) є миттєвими показниками, тобто їхні значення можна визначити (виміряти) в будь-який момент часу t. Випуск секторів, інвестиції (X_i, I_i)є показниками типу потоку, тобто їхні значення нагромад­жуються за рік, що розпочинається в момент t.

Отже, для зроблених припущень трисекторна модель економіки в абсолютних показниках набуває вигляду (2.1.39):

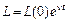
·	— кількість зайнятих;
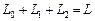
·	—розподіл зайнятих за секторами;
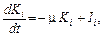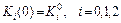
·	— динаміка фондів за секторами; (2.1.39)
· Xi = Fi (Ki, L i), i = 0, 1, 2	— випуск за секторами;
· X 1 = I 0 +I 1 + I 2	— розподіл продукції фондоутворювального сектора;
· X 0 = a 0 X 0 +a 1 X 1 + a 2 X 2	— розподіл продукції матеріального сектора,

де I_i — інвестиції у -й сектор; ν — темп приросту кількості зайнятих; μ _i –коефіцієнти вибуття ОВФ за секторами; a_i — коефіцієнти прямих матеріальних витрат за секторами.

Трисекторна модель є динамічною, оскільки містить чотири лінійні динамічні елементи. Вона нелінійна, оскільки випуски сек­торів задано нелінійними виробничими функціями.

У відносних показниках модель набуває форми:

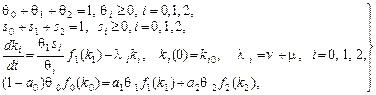(2.1.40)

де — частка числа зайнятих у і -му секторі із загальної кіль­кості зайнятих;

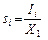— частка інвестицій у і –й сектор у загальному обсязі інвестицій;

— продуктивність праці в і - му секторі;

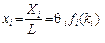народногосподарська продуктивність і -го сектора.

У моделі (2.1.40) параметри а ₀, а ₁, а ₂, μ₀, μ₁ ,μ₂, ν є екзогенними та вважаються сталими. Параметри (θ, s) = (θ₀, θ₁, θ₂, s ₀, s ₁, s ₂) — єкерівними. Рівняння для фондоозброєності має таку стаціонарну точку за умови, що (θ, s) постійні:

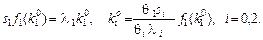
За k_i < k_i ⁰, як видно з (2.1.40), 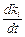> 0, а за k_i > k_i ⁰значення 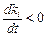, тому 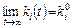, (за k_і0 < k_і ⁰є зростаючими, фондоозброєність наближається до стаціонарного значення, а за k_{і 0} > k_і ⁰ — спадними). Шляхом регульованого перерозподілу праці можна забезпечити монотонне наближення фондоозброєності до стаціонарного значення.

Дата добавления: 2014-11-08