
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тепер та
|
|
|
|
Динамічним або часовим рядом (time series) будемо називати послідовність спостережень, отриманих у рівновіддалені моменти часу, а відповідну йому ймовірнісну модель — дискретним випадковим або однофакторним стохастичним процесом.
Оскільки випадковий дискретний процес являє собою сукупність випадкових величин, то його найповнішою статистичною характеристикою є сумісна функція розподілу, або функція щільності розподілу. Щоб задати всі ймовірнісні властивості часового ряду, потрібна сукупність функцій розподілу, а саме одновимірна, двовимірна, тривимірна функції розподілу тощо: 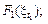

 . Індекси у величин
. Індекси у величин 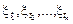 означають, що випадкові величини розглядаються в моменти часу
означають, що випадкові величини розглядаються в моменти часу  і вони мають сумісну функцію розподілу. Якщо взяти інші моменти часу, то функція розподілу буде іншою. Така сукупність функцій розподілу цілковито характеризує випадковий процес.
і вони мають сумісну функцію розподілу. Якщо взяти інші моменти часу, то функція розподілу буде іншою. Така сукупність функцій розподілу цілковито характеризує випадковий процес.
Стаціонарні процеси. Економетричне моделювання відбувається, як правило, на підставі лише однієї реалізації випадкового процесу, тож ясно, що про оцінювання сукупності всіх функцій розподілу взагалі годі казати. Окрім того, якщо процес поводиться так, що його основні статистичні характеристики з часом змінюються, то за короткий проміжок часу спостережень про нього взагалі нічого не можна сказати. Проблема втрачає гостроту, якщо розглядати вужчий клас випадкових процесів, який дістав назву стаціонарних випадкових процесів. Під стаціонарністю розуміють такі випадкові процеси, деякі властивості яких не змінюються з часом.
Однією з важливіших властивостей стаціонарного випад-
кового процесу є ергодичність. Вона полягає в тому, що кож-
на окрема реалізація випадкового процесу є так би мовити «повноважним» представником усієї сукупності можливих реалі-
зацій. Звідси для ергодичних процесів основні характеристи-
ки можна приблизно розраховувати не за кількома реаліза-
ціями, як це робиться в загальному випадку, а за будь-якою однією реалізацією за доволі тривалий проміжок часу. В практичних розрахунках розглядають стаціонарний процес у широкому сенсі.
Стаціонарний часовий ряд у широкому сенсі — це процес, для якого математичне сподівання та дисперсія існують і є сталими величинами, що не змінюються в часі, а автокореляційна (автоковаріаційна) функція залежить лише від різниці між двома моментами часу  і не залежить від конкретного періоду часу. Тобто для реалізації випадкового процесу
і не залежить від конкретного періоду часу. Тобто для реалізації випадкового процесу  основні моменти залишаються постійними й обмеженими у разі зміні часу
основні моменти залишаються постійними й обмеженими у разі зміні часу  , для якого вони розраховуються, а саме:
, для якого вони розраховуються, а саме:
математичне сподівання:  , для всіх
, для всіх  ;
;
дисперсія:  , для всіх
, для всіх  ;
;
автоковаріація порядку 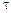 :
:
 ,
,
для всіх  .
.
Для отримання практичних оцінок часових рядів користуються такими формулами:
математичне сподівання:  ;
;
дисперсія: 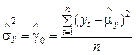 ; (1.2.7)
; (1.2.7)
автоковаріація порядку 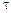 :
:  .
.
Зрушення в часі 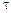 називають часовим лагом. Зауважимо, що
називають часовим лагом. Зауважимо, що 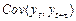 ,коли
,коли  = 0, дорівнює дисперсії:
= 0, дорівнює дисперсії: 

 . При цьому
. При цьому  . Можна розглядати функцію
. Можна розглядати функцію  як усі можливі значення автоковаріацій, де
як усі можливі значення автоковаріацій, де 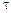 перебирає цілочисельні значення від
перебирає цілочисельні значення від  до
до 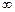 . Сукупність значень автоковаріацій за всіх можливих значень
. Сукупність значень автоковаріацій за всіх можливих значень 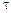 називають автоковаріаційною функцією випадкового процесу. Автоковаріаційна функціястаціонарного часового ряду залежить лише від різниць моментів часу (
називають автоковаріаційною функцією випадкового процесу. Автоковаріаційна функціястаціонарного часового ряду залежить лише від різниць моментів часу ( ). Ця функція парна, і досить розглядати невід’ємні
). Ця функція парна, і досить розглядати невід’ємні 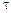 .
.
Коефіцієнт автокореляції між зрушеними на 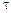 рівнями часового ряду — це автоковаріація, розділена на корінь із добутку двох дисперсій, та оскільки дисперсія стала, отримуємо просто
рівнями часового ряду — це автоковаріація, розділена на корінь із добутку двох дисперсій, та оскільки дисперсія стала, отримуємо просто  або
або 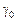 . Розраховують коефіцієнт автокореляції за формулою:
. Розраховують коефіцієнт автокореляції за формулою:
 . (1.2.8)
. (1.2.8)
Вираз (1.2.8) визначає автокореляційну функцію (АКФ)часового ряду, яка показує наскільки статистично залежними є значення часового ряду для різних зрушень 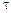 у часі (наприклад, для річних спостережень рік чи два роки тощо).Автокореляційна функція стаціонарного часового ряду залежить лише від різниці між двома моментами часу
у часі (наприклад, для річних спостережень рік чи два роки тощо).Автокореляційна функція стаціонарного часового ряду залежить лише від різниці між двома моментами часу  , і є парною функцією, тобто
, і є парною функцією, тобто  . Задаючи різні значення
. Задаючи різні значення 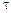 = 1, 2, 3,..., отримують послідовність значень
= 1, 2, 3,..., отримують послідовність значень 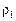 ,
,  ,
, 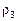 , ... Графік автокореляційної функції називають корелограмою. За корелограмою можна визначити запізнення, із яким зміна показника
, ... Графік автокореляційної функції називають корелограмою. За корелограмою можна визначити запізнення, із яким зміна показника 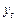 позначається на його наступних значеннях.
позначається на його наступних значеннях.
У широкому сенсі оцінки наведених статистик є консистентними, тобто для них існує межа щодо ймовірності, яка збігається з їхніми справжніми значеннями для генеральної сукупності. Далі замість стаціонарності в широкому сенсі будемо просто говорити стаціонарність, оскільки інші різновиди стаціонарності не розглядатимуться.
Оптимальний предиктор і його властивості. Практика розроблення різноманітних прогнозів спирається на цілу систему методів, які стосуються оцінювання (прогнозування) величин, недоступних для безпосереднього спостереження в конкретний момент, і їх потрібно знайти за допомогою доступних для вимірювання (спостереження) супровідних величин.
Завдання стохастичного прогнозування полягає в тому, щоб за відомою сукупністю спостережень 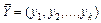 за випадковими величинами побудувати таку функцію від цих величин, яку можна було б використати для оцінювання прогнозованої величини
за випадковими величинами побудувати таку функцію від цих величин, яку можна було б використати для оцінювання прогнозованої величини  . При цьому
. При цьому 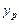 та
та  стохастично пов’язані, тобто мають сумісну щільність розподілу
стохастично пов’язані, тобто мають сумісну щільність розподілу  . Наприклад,
. Наприклад, 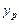 належить до майбутнього, а
належить до майбутнього, а  — до теперішнього. Функцію
— до теперішнього. Функцію 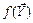 називають предиктором величини
називають предиктором величини 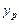 за
за 
Для вимірювання точності предиктора, як правило, використовують середньоквадратичну похибку  . Предиктор, який мінімізує
. Предиктор, який мінімізує  в заданому класі предикторів, називають оптимальним предиктором, або прогнозом. Розроблення методів побудови оптимальних предикторів становить зміст стохастичного прогнозування.На підставі предиктора, можна одержати варіанти прогнозу, що відповідатимуть сформульованим гіпотезам та умовам, урахованим під час його побудови.
в заданому класі предикторів, називають оптимальним предиктором, або прогнозом. Розроблення методів побудови оптимальних предикторів становить зміст стохастичного прогнозування.На підставі предиктора, можна одержати варіанти прогнозу, що відповідатимуть сформульованим гіпотезам та умовам, урахованим під час його побудови.
Теорія стохастичного прогнозування величини 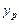 за супровідними величинами
за супровідними величинами  передбачає, що сумісний закон розподілу
передбачає, що сумісний закон розподілу  — відомий. У практичному застосуванні точний вид залежності між
— відомий. У практичному застосуванні точний вид залежності між 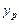 та
та  найчастіше невідомий і пошук найкращого предиктора обмежується лінійними прогнозами, тобто коли
найчастіше невідомий і пошук найкращого предиктора обмежується лінійними прогнозами, тобто коли  . Тоді оптимальний лінійний предиктор існує та збігається із функцією регресії
. Тоді оптимальний лінійний предиктор існує та збігається із функцією регресії 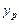 на
на  , тобто задається як умовне математичне сподівання1:
, тобто задається як умовне математичне сподівання1:
 .
.
Ця функція має максимальну кореляцію з 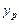 серед усіх лінійних предикторів. Для побудови оптимального предиктора досить знати перші та другі моменти початкового розподілу
серед усіх лінійних предикторів. Для побудови оптимального предиктора досить знати перші та другі моменти початкового розподілу  , які знаходять шляхом оброблення результатів відомих спостережень. Підставляючи ці оцінки замість теоретичних характеристик, отримують емпіричний предиктор, який використовують для прогнозування майбутніх значень
, які знаходять шляхом оброблення результатів відомих спостережень. Підставляючи ці оцінки замість теоретичних характеристик, отримують емпіричний предиктор, який використовують для прогнозування майбутніх значень 
Отже, головну роль у статистичному підході до прогнозування відіграє вибір відповідної моделі. В разі наповнення її числовими параметрами вона стає безпосереднім інструментом прогнозування — предиктором.
Білий шум (White noise). Білим шумом називають часові ряди, рівні яких мають середню, що дорівнює нулю, сталу дисперсію та нульову коваріацію послідовних спостережень, тобто нульову автокореляцію. Наприклад, залишки регресії, що задовольняють умовам теореми Гауса-Маркова, є «білим шумом»:  ;
; 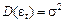 ;
;  за
за  .
.
Наведене визначеннябілого шуму характеризує його як стаціонарний ряд. Хоча стаціонарний ряд необов’язково буде білим шумом, оскільки може мати середню або коваріацію, відмінні від нуля.
Якщо  ~
~  , то йдеться про гаусівський білий шум, хоча змінна білого шуму не обов’язково підпорядковується закону нормального розподілу. Найкращим передбаченням або прогнозом білого шуму є його нульове середнє значення. Білий шум відіграє важливу роль в аналізі часових рядів. На практиці білий шум трапляється не надто часто, але він утворює складніші процеси. Прикладом цього є процес випадкового блукання.
, то йдеться про гаусівський білий шум, хоча змінна білого шуму не обов’язково підпорядковується закону нормального розподілу. Найкращим передбаченням або прогнозом білого шуму є його нульове середнє значення. Білий шум відіграє важливу роль в аналізі часових рядів. На практиці білий шум трапляється не надто часто, але він утворює складніші процеси. Прикладом цього є процес випадкового блукання.
Випадкове блукання (Random walk). Іноді його називають броунівським рухом. Це стохастичний процес, де зміна рівня ряду, скажімо, рівня інфляції, досягається додаванням до нього випадкової змінної e t із постійною дисперсією та середнім, що дорівнює нулю. Випадкове блукання задається так:
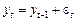 , (1.2.9)
, (1.2.9)
де  — білий шум. Цей процес можна розглядати як авторегресію із коефіцієнтом 1. Зазначимо, що лише
— білий шум. Цей процес можна розглядати як авторегресію із коефіцієнтом 1. Зазначимо, що лише  має нульову середню та постійну дисперсію.
має нульову середню та постійну дисперсію.
Термін «випадкове блукання» виник у зв’язку із жартівливою задачкою: якщо в поле випустити п’яного, то де він опиниться через деякий час? Результат — якщо п’яний блукає випадково, то його слід очікувати на тому самому місці, тобто в середньому його місцезнаходження не зміниться.
За умови наявності певної початкової точки 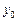 підстановка у (1.2.9) значень змінної за попередні моменти часу дає вираз
підстановка у (1.2.9) значень змінної за попередні моменти часу дає вираз 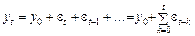 , який за t, що прямує до нескінченності, включатиме необмежену кількість доданків
, який за t, що прямує до нескінченності, включатиме необмежену кількість доданків  , кожен із яких має нульове математичне сподівання та ненульову дисперсію
, кожен із яких має нульове математичне сподівання та ненульову дисперсію 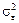 .
.
Обрахуємо математичне сподівання процесу випадкового блукання: 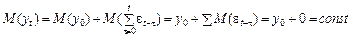 , тобто математичне сподівання задовольняє умові стаціонарності.
, тобто математичне сподівання задовольняє умові стаціонарності.
Дисперсія процесу випадкового блукання дорівнює  :
:  . Після розкриття дужок подвоєні добутки після взяття математичного сподівання будуть дорівнювати нулю, і залишиться математичне сподівання суми квадратів. Ураховуючи властивості дисперсії білого шуму, одержимо
. Після розкриття дужок подвоєні добутки після взяття математичного сподівання будуть дорівнювати нулю, і залишиться математичне сподівання суми квадратів. Ураховуючи властивості дисперсії білого шуму, одержимо  . Отже, процес випадкового блукання не стаціонарний, оскільки дисперсія
. Отже, процес випадкового блукання не стаціонарний, оскільки дисперсія 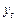 зростає з часом.
зростає з часом.
Прогноз такого процесу на 1 крок уперед дорівнює 
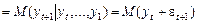 . Але
. Але  незалежно від
незалежно від 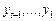 . Отже прогноз на крок уперед становить:
. Отже прогноз на крок уперед становить: 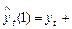
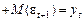 . На два кроки уперед:
. На два кроки уперед: 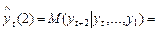
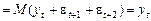 тощо. Прогноз на
тощо. Прогноз на 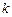 кроків уперед становитиме:
кроків уперед становитиме:
 .
.
Хоча величина прогнозної оцінки зі зростанням періоду випередження прогнозу 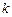 залишається постійною, дисперсія помилки прогнозу зростає. Так, помилка прогнозу на один крок вперед дорівнює
залишається постійною, дисперсія помилки прогнозу зростає. Так, помилка прогнозу на один крок вперед дорівнює 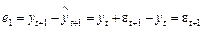 та її дисперсія дорівнює
та її дисперсія дорівнює 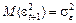 . Для прогнозу на два кроки вперед —
. Для прогнозу на два кроки вперед — 
 , а дисперсія —
, а дисперсія —  , оскільки
, оскільки  та
та 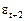 — незалежні. Аналогічно для прогнозу на
— незалежні. Аналогічно для прогнозу на 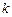 кроків уперед дисперсія помилки прогнозу становитиме
кроків уперед дисперсія помилки прогнозу становитиме  . Середньоквадратичне відхилення прогнозу зростає пропорційно
. Середньоквадратичне відхилення прогнозу зростає пропорційно  , і можна оцінити інтервал надійності прогнозу.
, і можна оцінити інтервал надійності прогнозу.
Якщо рівняння 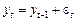 , де збурення
, де збурення  є білим шумом, переписати як
є білим шумом, переписати як  , отримаємо процес білого шуму. Приріст, або першу різницю (first difference), можна розглядати як інший часовий ряд
, отримаємо процес білого шуму. Приріст, або першу різницю (first difference), можна розглядати як інший часовий ряд 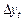 , який є стаціонарним. Перехід до перших різниць є розповсюдженим засобом зведення нестаціонарного часового ряду до стаціонарного.
, який є стаціонарним. Перехід до перших різниць є розповсюдженим засобом зведення нестаціонарного часового ряду до стаціонарного.
Іноді випадкове блукання може передбачати елемент зсунення. Зсунення означає тенденцію (дрейф). Отже, випадкове блукання зі зсуненням — це випадкове блукання із дрейфом. Наприклад:
 , (1.2.10)
, (1.2.10)
де 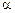 — стала величина.
— стала величина.
Середньоквадратичне відхилення прогнозу в цьому разі не зміниться, оскільки: 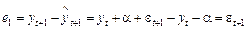 .
.
Прогноз зростає лінійно за 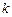 , а інтервал надійності прогнозу розширюється пропорційно
, а інтервал надійності прогнозу розширюється пропорційно  .
.
Середнє значення перших різниць становить швидкість зростання фактичного ряду спостережень, при цьому кожна зміна 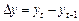 не залежить від усіх попередніх змін і має ідентичний розподіл імовірностей..
не залежить від усіх попередніх змін і має ідентичний розподіл імовірностей..
Марківський процес. Марківськими називають процеси, в яких стан об’єкта в кожен наступний момент часу визначається станом поточного моменту і не залежить від того, яким шляхом об’єкт досяг поточного стану. Це стаціонарна послідовність незалежних, однаково розподілених випадкових величин. У термінах кореляційного аналізу часових рядів марківський процес можна описати таким чином: існує статистично значущий кореляційний зв’язок початкового ряду із рядом, зрушеним на один часовий інтервал, і цей зв’язок відсутній із рядами, зрушеними на два, три тощо часові інтервали. В ідеальному випадку ці коефіцієнти кореляції дорівнюють нулю.
За допомогою рівняння авторегресії такий ряд можна представити як:
 або
або  , (1.2.11)
, (1.2.11)
розкладаючи  , отримуємо:
, отримуємо: 
 тощо. Очевидно, що
тощо. Очевидно, що 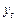 залежить від усіх ми-
залежить від усіх ми-
нулих (але не майбутніх)  . Якщо
. Якщо  , то й
, то й 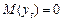 . Знайдемо добуток (1.2.11) на
. Знайдемо добуток (1.2.11) на  і визначимо математичне сподівання:
і визначимо математичне сподівання:
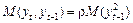 або
або 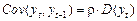 ,
,
остаточно  , тобто
, тобто 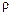 є першою автокореляцією процесу.
є першою автокореляцією процесу.
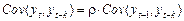 розділимо на
розділимо на 
 :
:  .
.
Отже, всі кореляції марківського процесу можна виразити через першу автокореляцію.
Окрім марківських з-поміж стаціонарних процесів авторегресії часто трапляються процеси Юла, в яких ураховано авторегресію не лише першого, а й другого порядку, тобто 
 .
.
Розкладення (декомпозиція) часового ряду. Реальні часові ряди в економіці, як правило, є динамічно нестабільними, отже — не стаціонарними, і поняття стаціонарності процесу часто є лише зручною абстракцією для застосування статистичних методів. Кожен рівень часового ряду формується під впливом великої кількості чинників, які відображають закономірність і випадковість його формування. В аналізі часових рядів прийнято представляти часовий ряд 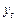 у вигляді суми систематичної складової (середньої) та випадкового відхилення від неї:
у вигляді суми систематичної складової (середньої) та випадкового відхилення від неї:
 , (1.2.12)
, (1.2.12)
де  — невипадкова функція часу (детермінована частина);
— невипадкова функція часу (детермінована частина);
 — випадкова, недетермінована частина.
— випадкова, недетермінована частина.
Завдання розкладення часового ряду полягає в аналізі чинників, що впливають на значення його рівнів, у вирізненні серед них головних і другорядних (випадкових), а потім серед головних — еволюційних та періодичних (сезонних тощо).
· Еволюційні чинники визначають загальний напрям розвитку економічного показника, провідну його тенденцію. Тенденція — це невипадкова складова часового ряду, яка змінюється повільно, і описується за допомогою певної функції 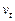 , яку називають функцією тренду або просто трендом. Тренд відображає вплив на економічний показник деяких постійних чинників, дія яких акумулюється в часі. У широкому сенсі під трендом розуміють будь-який упорядкований процес, що відрізняється від випадкового, тобто функцію
, яку називають функцією тренду або просто трендом. Тренд відображає вплив на економічний показник деяких постійних чинників, дія яких акумулюється в часі. У широкому сенсі під трендом розуміють будь-який упорядкований процес, що відрізняється від випадкового, тобто функцію  у (1.2.12). Іноді під трендом розуміють також зміщення у часі математичного сподівання. Відносно
у (1.2.12). Іноді під трендом розуміють також зміщення у часі математичного сподівання. Відносно  припускається, що це певна гладка функція, ступінь гладкості якої заздалегідь не відомий. Під ступенем гладкості розуміють мінімальний ступінь поліному, що найкраще згладжує компоненту
припускається, що це певна гладка функція, ступінь гладкості якої заздалегідь не відомий. Під ступенем гладкості розуміють мінімальний ступінь поліному, що найкраще згладжує компоненту 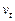 .На рис. 1.2.4 а) зображено умовний часовий ряд із тенденцією, що лінійно зростає.
.На рис. 1.2.4 а) зображено умовний часовий ряд із тенденцією, що лінійно зростає.
· Серед чинників, щовизначають регулярні коливання ряду, розрізняють такі:
Сезонні, щовідповідають коливанням, які мають періодичний або близький до нього характер упродовж одного року. Наприклад, ціни на сільгосппродукцію взимку вищі, ніж улітку; рівень безробіття в курортних містах у зимовий період зростає відносно до літнього. Сезонні чинники можуть охоплювати причини, пов’язані з діяльністю людини (свята, відпуст-
ки, релігійні традиції тощо). Так, у ряду щомісячних даних слід очікувати наявності сезонних коливань із періодом 12, у квартальних рядах — із періодом 4. На рис. 1.2.4 б) зображено умовний часовий ряд, який містить лише сезонну компоненту.
Результат дії сезонних чинників моделюють за допомогою функції 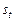 .
.
Циклічні (кон’юнктурні)коливання схожі на сезонні, але виявляються на триваліших інтервалах часу. Циклічні коливання пояснюються дією довготермінових циклів економічної, демографічної або астрофізичної природи. Наприклад, за багаторічними спостереженнями активність сонця має циклічність у 10,5—11 років, причому сплески сонячної радіаціївпливають на врожайність зернових культур, репродуктивну властивість тварин тощо. Отже динаміка показника міситиме характерні зміни, що повторюються з однаковою циклічністю. Результат дії циклічних чинників моделюють за допомогою функції  .
.
Тренд, сезонна й циклічна компоненти не є випадковими, тому їх називають систематичними компонентами часового ряду.
· Випадкові чинники не підлягають вимірюванню, але неминуче супроводжують будь-який економічний процес і визначають стохастичний характер його елементів. До випадкових чинників можна віднести помилки вимірювання, випадкові збурення тощо. Деякі часові ряди, наприклад стаціонарні, не мають тенденції та сезонної складової, кожен наступний рівень їх утворюється як сума середнього рівня ряду і випадкової (додатної або від’ємної) компоненти. Приклад такого ряду демонструє рис. 1.2.4 в). Результат впливу випадкових чинників позначається випадковою компонентою ε t, яку обчислюють як залишок або похибку, що залишається після вилучення з часового ряду систематичних компонент. Це не означає, що така складова не підлягає подальшому аналізу, оскільки містить лише хаос.
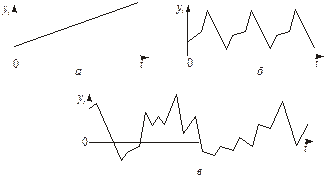
Рис. 1.2.4. Головні компоненти часового ряду:
а — тренд, що зростає; б — сезонна компонента;
в —випадкова компонента
За декомпозицією Вольда суто недетермінований стаціонарний у широкому сенсі випадковий процес можна записати у
вигляді:
 , (1.2.13)
, (1.2.13)
де  — детермінована складова або математичне сподівання цього процесу,
— детермінована складова або математичне сподівання цього процесу,  — білий шум з обмеженими математичним сподіванням та дисперсією. Розкладення Вольда (1.2.13) ще називають лінійним фільтром, начебто білий шум пропустили крізь лінійний фільтр. Це означає, що, не втрачаючи цілого, обмежуються зручним лінійним представленням і переходять до вивчення стаціонарних процесів.
— білий шум з обмеженими математичним сподіванням та дисперсією. Розкладення Вольда (1.2.13) ще називають лінійним фільтром, начебто білий шум пропустили крізь лінійний фільтр. Це означає, що, не втрачаючи цілого, обмежуються зручним лінійним представленням і переходять до вивчення стаціонарних процесів.
Щоб вираз (1.2.13) мав сенс, повинна виконуватися умова збіжності за ймовірністю, оскільки підсумовуються випадкові величини. Ця умова записується, як 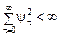 . Припускається, що
. Припускається, що  . Чим більший ваговий коефіцієнт
. Чим більший ваговий коефіцієнт  , тим більший вплив випадкового збурення в момент
, тим більший вплив випадкового збурення в момент  на поточний момент t.
на поточний момент t.
Аналіз випадкової компоненти є важливою інформативною частиною дослідження часових рядів. Пояснюється це тим, що в короткотерміновому та певною мірою середньотерміновому прогнозуванні результати прогнозу тісно пов’язані із випадковою компонентою, тоді як у довготерміновому прогнозуванні головну увагу приділяють визначенню тенденції й взаємозв’язків між чинниками.
Очевидно, реальні дані цілковито не відповідають лише одній із наведених функцій, тож часовий ряд 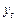 ,
,  можна уявити у вигляді розкладення:
можна уявити у вигляді розкладення:
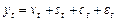 ,
,  (1.2.14)
(1.2.14)
або різноманітних поєднань окремих функцій. Однак завжди припускають обов’язкову наявність випадкової складової. Розкладення (декомпозиція) часового ряду відбувається за такими варіантами моделей:
модель тренду 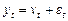 ,
,  ; (1.2.15)
; (1.2.15)
модель сезонності  ,
,  ; (1.2.16)
; (1.2.16)
тренд-сезонна модель  ,
,  . (1.2.17)
. (1.2.17)
Моделі тренду й сезонності (тренд-сезонні) можуть відображати як відносно постійну сезонну хвилю (цикл), так і динамічно змінювану залежно від тренду. Перша форма — (1.2.14—1.2.17) належить до адитивних, друга (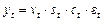 ,
,  , (1.2.18)) — до мультиплікативних моделей.
, (1.2.18)) — до мультиплікативних моделей.
Моделі для врахування циклічних чинників будують аналогічно до тренд-сезонних, тільки замість сезонної складової вводять циклічну.
Процес окремого обчислення функцій 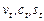 і
і  називають фільтрацією компонент часового ряду
називають фільтрацією компонент часового ряду 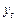 . Процедура оцінювання детермінованої частини разом з усіма невипадковими компонентами має назву згладжування часового ряду.
. Процедура оцінювання детермінованої частини разом з усіма невипадковими компонентами має назву згладжування часового ряду.
Успішне розв’язання завдань виявлення й моделювання дії розглянутих складових чинників є підґрунтям, відправним пунктом для зрозуміння механізму формування соціально-економічного процесу та його прогнозування.
Утім, слід пам’ятати, що операція розкладення часового ряду, яка є допустимою з математичної точки зору й корисною для моделювання динаміки зміни показників у часі, подеколи може ввести в оману. Зокрема, за такого підходу дуже спрощеним може виявитися припущення стосовно незалежного впливу названих компонент, їхньої чіткої структури.
Типи нестаціонарних часових рядів. За видом нестаціонарності часові ряди, що застосовують в економічній практиці, розподіляють на ряди типу: TS, DS, тренд-сезонні, нелінійні.
Часовий ряд типу TS (trend stationary process). До цього типу відносять нестаціонарні часові ряди із детермінованим поліноміальним трендом 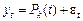 , де
, де  поліном ступеня
поліном ступеня 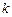 від
від 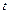 , а
, а  — стаціонарний процес, який не обов’язково є білим шумом. Наприклад, простий лінійний тренд
— стаціонарний процес, який не обов’язково є білим шумом. Наприклад, простий лінійний тренд  . Тут нестаціонарна змінна
. Тут нестаціонарна змінна 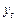 виражена через детермінований, тобто невипадковий тренд. Попри те, що додавання стаціонарної змінної призводить до коливань навколо тренду й робить
виражена через детермінований, тобто невипадковий тренд. Попри те, що додавання стаціонарної змінної призводить до коливань навколо тренду й робить 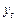 випадковою, ми, власне, маємо інформацію тільки про середнє значення
випадковою, ми, власне, маємо інформацію тільки про середнє значення  , тобто часовий ряд характеризується наявністю тренду в середньому значенні. Отже, ані поточна, ані минулі події не змінюють довготермінових прогнозів цього процесу. Вплив випадкового збурення
, тобто часовий ряд характеризується наявністю тренду в середньому значенні. Отже, ані поточна, ані минулі події не змінюють довготермінових прогнозів цього процесу. Вплив випадкового збурення  (поточний шок) забувається одразу на наступному кроці (
(поточний шок) забувається одразу на наступному кроці (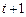 ). Похибка довготермінового прогнозу буде мати обмежену дисперсію
). Похибка довготермінового прогнозу буде мати обмежену дисперсію  , тому невизначеність є обмеженою навіть у далекому майбутньому.
, тому невизначеність є обмеженою навіть у далекому майбутньому.
Нестаціонарний процес типу TS зводять до стаціонарного за допомогою кількох методів. Наприклад, для лінійного тренду  перехід до стаціонарності може відбуватися:
перехід до стаціонарності може відбуватися:
· шляхом виділення лінійного тренду. Наприклад, будують лінійну регресію за часом і розглядають стаціонарний залишок  ;
;
· узяттям перших різниць: різниці двох суміжних рівнів часового ряду
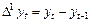 (1.2.20)
(1.2.20)
є першими різницями ряду 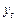 , або
, або 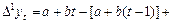
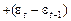 . Звідси
. Звідси 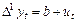 , де
, де 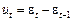 — випадкова величина, розподіл якої цілком визначається розподілом величини
— випадкова величина, розподіл якої цілком визначається розподілом величини  . Окрім того, перші різниці часового ряду з лінійною тенденцією мають постійне математичне сподівання, що дорівнює певній константі
. Окрім того, перші різниці часового ряду з лінійною тенденцією мають постійне математичне сподівання, що дорівнює певній константі  , не залежній від
, не залежній від  .
.
Загалом якщо часовий ряд має тенденцію, що виражається через поліном ступеня  , то різниці порядку
, то різниці порядку 
 (1.2.21)
(1.2.21)
є випадковими величинами з постійним математичним сподіванням. У цьому разі 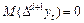 .
.
Якщо тенденція часового ряду відповідає експоненціальному або степеневому тренду, то метод послідовних різниць слід застосовувати не до початкового ряду, а до його логарифмів. Наприклад, процес у своєму розвитку наближається до певної величини  та може бути представлений у вигляді
та може бути представлений у вигляді
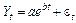 ,
,  , (1.2.22)
, (1.2.22)
де  — аналогічна (1.2.20). Тоді процес, утворений із величин
— аналогічна (1.2.20). Тоді процес, утворений із величин  , має постійне середнє (
, має постійне середнє ( ) і може бути зведений до стаціонарного процесу авторегресії.
) і може бути зведений до стаціонарного процесу авторегресії.
Часовий ряд типу DS (differencing stationary process). Це ряди без періодичної складової та тенденції зростання, але наявність тренду в дисперсії засвідчує їхню нестаціонарність. Прикладом таких рядів є процес випадкового блукання 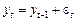 . Як уже зазначалося, цей процес накопичує випадкові збурення від усіх попередніх шоків, тобто має нескінченну пам’ять. Такий процес описують стохастичним трендом і зводять до стаціонарного шляхом узяття першої різниці, звідси й відповідна назва.
. Як уже зазначалося, цей процес накопичує випадкові збурення від усіх попередніх шоків, тобто має нескінченну пам’ять. Такий процес описують стохастичним трендом і зводять до стаціонарного шляхом узяття першої різниці, звідси й відповідна назва.
Тренд-сезонні часові ряди окрім тренду містять чітко виражені сезонні коливання, які, своєю чергою, спричинюють нестаціонарність. Якщо процес включає періодичні (сезонні) коливання навколо середнього значення з періодом 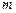 , тобто
, тобто
 (1.2.23)
(1.2.23)
із точністю до випадкової складової, то d цьому разі різниці через 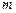 часових інтервалів представляють стаціонарний процес
часових інтервалів представляють стаціонарний процес
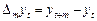 ,
,  де
де 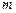 —
—  , (1.2.24)
, (1.2.24)
середнє значення якого збігається із середнім значенням початкового ряду.
Амплітуда сезонних коливань може зростати з часом і не обов’язково лінійно. Ці ряди характеризуються наявністю тренду в середньому значенні й дисперсії.
Нелінійні динамічні процеси. До цього типу відносять часові ряди зі складною структурою, вони мають тренд і містять різні види коливань, зокрема сезонні та циклічні. Структуру таких рядів узагалі не можна описати за допомогою відомих функцій, оскільки для різних ділянок часового ряду набір цих функцій буде різним, тобто в цьому разі можна говорити про ряди зі змінною структурою, які характерні для нелінійних динамічних процесів. Вони спостерігаються в динаміці цін на ринках капіталу тощо.
Лише в останні роки завдяки розвитку математичних методів нелінійної динаміки та комп’ютерних технологій з’явилася можливість досліджувати такі процеси. У певному аспекті [29] будь-який динамічний процес зрештою є детермінованим, і моделювання його як реалізації випадкового процесу є зручним спрощенням. Невипадковий часовий ряд відображає невипадкову природу впливів. Стрибки даних відповідають стрибкам впливових чинників і відбивають властиву їм кореляцію. Детерміновані процеси, що виглядають як випадкові, у теорії нелінійностей називають детермінованим хаосом. Добре відомо, що просте детерміноване нелінійне різницеве рівняння може породжувати надзвичайно складні часові траєкторії, які видаються випадковими. Наприклад, рівняння, яке трапляється в аналізі фінансових ринків  , де
, де 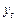 є ціною облігацій. У багатьох економічних застосуваннях значення параметру
є ціною облігацій. У багатьох економічних застосуваннях значення параметру 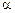 лежить між 1 та 4, таким чином виключають від’ємні значення рівноваги для
лежить між 1 та 4, таким чином виключають від’ємні значення рівноваги для 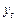 і уникають прямування процесу до нескінченності. За зміни
і уникають прямування процесу до нескінченності. За зміни 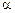 від 1 до 4 динаміка системи зазнає суттєвих змін. Наприклад, для 1 <
від 1 до 4 динаміка системи зазнає суттєвих змін. Наприклад, для 1 < 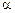 < 3, за будь-яким відхиленням від
< 3, за будь-яким відхиленням від 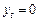 , динаміка процесу прямує до рівноваги
, динаміка процесу прямує до рівноваги  . Разом із тим для 3,75 <
. Разом із тим для 3,75 < 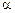 < 4 спостерігатиметься нескінченна кількість циклів із різною періодичністю і нескінченне число положень рівноваги з еволюцією процесу залежно від початкового його стану. Такий тип поведінки називають «хаосом». Властивістю цього процесу є те, що хоча він детермінований, випадкове блукання є задовільною моделлю для описання механізму породження даних. У цьому випадку зміни
< 4 спостерігатиметься нескінченна кількість циклів із різною періодичністю і нескінченне число положень рівноваги з еволюцією процесу залежно від початкового його стану. Такий тип поведінки називають «хаосом». Властивістю цього процесу є те, що хоча він детермінований, випадкове блукання є задовільною моделлю для описання механізму породження даних. У цьому випадку зміни 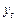 неможливо передбачити, хоча всю траєкторію перебігу процесу цілком можна передбачити.
неможливо передбачити, хоча всю траєкторію перебігу процесу цілком можна передбачити.
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 1477; Нарушение авторских прав?; Мы поможем в написании вашей работы!