Лекція 19

Модель з лінійним трендом та дрейфом (). Для цього розподілу критичне значення DF позначимо. Нульова гіпотеза означає, що ряд — це випадкове блукання із двома типами тренду: стохастичним та детермінованим, тобто є нестаціонарним процесом ~.

Модель тільки із додатною середньою (). Критичне значення DF —. Нульова гіпотеза означає, що і ряд — це випадкове блукання із дрейфом, тобто є нестаціонарним процесом: ~.

Нульова гіпотеза буде відхилена, якщо t -відношення 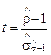має від’ємне значення, менше за критичне із таблиць МакКіннона. У цьому випадку часовий ряд 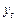— стаціонарний: 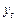~ 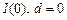або має лінійний тренд () і після його вилучення стає стаціонарним.

Розширений АDF-тест. Його використання базується на припущенні, що замість білого шуму в моделі (1.3.12) випадкова складова є стаціонарним авторегресійним процесом, наприклад, типу марківського, або у загальному випадку — типу ARMA (p, q). Тоді досліджується таке рівняння:

. (1.3.12)

В АDF -тесті перевіряється значущість лише одного коефіцієнта — . Наявність лагових прирощень 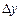та лагових значень випадкової змінної не змінює розподілу, тож можна користуватися таблицями Мак-Кіннона, що й для DF -тесту. Якщо в моделі (1.3.14) присутні і вільний член, і тренд, то нульову гіпотезу мож­на перевіряти, використовуючи статистику 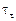; якщо лише вільний член 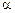, то статистику ; якщо немає жодного потрібно використовувати статистику .

Для можливості застосування АDF -тесту важливо перевірити, що дисперсія випадкової величини є сталою, тобто випадкові збурення гомоскедастичні. Інакше у випадку їх гетероскедастичності тест уже неможливо застосувати. У комп’ютерному пакеті Ekonometric Views реалізований непараметричний тест Філліпса-Перрона (РР -тест) цієї перевірки.

Наступною важливою проблемою є те, що АDF -тест дуже чутливий до правильного вибору значень та 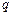, які точно не відомі. Існує кілька способів її розв’язання:

· застосувати правило узгодження кількості лагів, котрі
потрібно включати до моделі при застосуванні АDF -тесту, та довжиною часового ряду. В макроекономічних рядах, якщо маємо від 81 до 256 точок, потрібно включати три лага, якщо мен­ше 81 точки, то два лага. Для фінансових рядів спрацьовує наближення , де квадратні дужки означають цілу частину числа;

· залишати таку кількість лагів, для яких оцінки МНК-коефі­цієнтів у разі прирощень у (1.3.12) будуть статистично значущими за -розподілом Стьюдента;

застосувати економетричний пакет Ekonometric Views, який містить алгоритм вибору кількості лагів.

Модифікація критерію Дарбіна-Ватсона. Для часового ряду:

, (1.3.14)

де u є випадковим блуканням

, (1.3.15)

e _t — білий шум, оцінюють параметри й обчислюють статистику Дарбіна-Ватсона:

. (1.3.16)

Якщо запропонована модель (1.3.14) — (1.3.15) є коректною, з (1.3.16) очевидно, що чисельник у DW є сумою квадратів 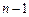доданків білого шуму, а знаменник є сумою п доданків, кожен із яких (рекурентною підстановкою замість u_{t – 1} у (1.3.5)) можна записати як нескінченну суму квадратів доданків білого шуму. Отже, значення статистики Дарбіна-Ватсона буде близьким до нуля, а критерій полягає у визначенні значущості його відмінності від нуля. Ця статистика називається коінтегративною регресійною статистикою Дарбіна-Ватсо­на (КРДВ), для якої розроблено таблиці критичних значень. Якщо для (1.3.14) статистика КРДВ не відмінна від нуля, доходять висновку, що 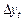є стаціонарним, а 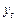є нестаціонарним І (1)-процесом.

Дослідження автокореляційної функцій часового ряду (АКФ). Перевірки часових рядів на стаціонарність вважаються недостатньо путижними, особливо у невеликих вибірках, ось чому дуже корисно додатково аналізувати корелограми, які є менш формальним апаратом перевірки на стаціонарність.

Властивістю автокореляційної функцій є те, що для стаціонар­них рядів існує таке значення К, що для 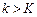коефіцієнти автокореляції 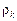приймають майже нульові значення. Отже, якщо зі збільшенням часового проміжку 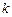АКФ ряду за абсолютним значенням поступово згасає, ряд можна вважати стаціонарним. Якщо поведінка автокореляційної функції не така, то вона не може бути автокореляційною функцією стаціонарного процесу. На практиці порядок 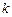АКФ рекомендується обирати від п /4 до п /3. Значення коефіцієнта автокореляції, близьке до одиниці, вказує на значну додатну залежність між фактичним рядом даних і рядом, зрушеним на 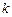одиниць часу. У цьому разі пари спостережень будуть близькими один до одного. Якщо з’ясується, що біль­ше спостереження утворює пару з меншим, то коефіцієнт автокореляції буде від’ємним і близьким до – 1. Для перевірки статистичної значущості коефіцієнтів автокореляції не існує простих критеріїв.

Перевірка за критерієм стандартної похибки коефіцієнта автокореляції. Якщо обсяг вибірки (п) великий, окремі (кожного порядку) коефіцієнти автокореляції випадкових даних мають вибірковий розподіл, який наближається до нормального з нульовим математичним сподіванням і середнім квадратичним відхиленням, що дорівнює

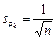. (1.3.17),

Якщо 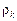виходить за межі інтервалу 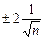, то часовий ряд має суттєву автокореляцію 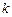-го порядку. Зазначимо: якщо обчис­лено 20 значень АКФ, то на 5-відсотковому рівні значущості в середньому один із 20 буде значущим. Цей факт разом із відносно малим обсягом вибірки на практиці означає, що критерій на підставі окремих коефіцієнтів може бути ненадійним. Альтернативою є використання критерію Бокса-Пірса.

Q — критерій Бокса-Пірса використовують для перевірки значущості всієї множини коефіцієнтів автокореляції як групи. Статистичний Q -критерій обчислюють за формулою:

, (1.3.18)

де 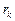— оцінка автокореляції порядку ;

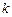т — найбільший лаг, що розглядається.

Якщо всі автокореляції до порядку т дорівнюють нулю, то Q має приблизно 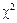-розподіл із т ступенів свободи. Велике значення Q порівняно з критичним зумовлює відхилення нульової гіпотези.

Існує кілька модифікацій цього критерію. Найпопулярнішим із них є критерій Льюнга-Бокса:

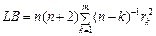. (1.3.19)

Комбінація лінійного та сезонно-адитивного тренду. Цей тип тренду може описувати також ситуацію суто сезонного тренду без лінійного елемента. Однак у загальному випадку для моделі цього типу характерна присутність сезонного тренду, який, своєю чергою, може лінійно зростати. Лінійний та сезонно-адитивний тренди зображено на рис. 1.3.12. Як бачимо, з року в рік повторюються два викиди.

Рис. 1.3.12. Динаміка попиту з лінійним трендом
і сезонно-адитивною складовою

Комбінація лінійного та сезонно-мультиплікативного трен­ду. Як і для комбінації лінійного та сезонно-адитивного трендів, аналітичне дослідження цього типу трендів передбачає і випадок суто сезонно-мультиплікативного тренду без лінійного зростання (рис. 1.3.13), і випадок лінійного зростання.

Статистичні методи визначення наявності нелінійної динаміки й детермінованого хаосу. Належність часового ряду до випадкового процесу або детермінованого хаосу можна визначити за допомогою методунормованого розмаху.

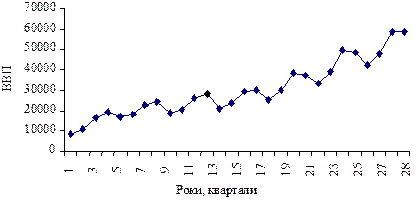
Рис. 1.3.13. Динаміка ВВП
із сезонно-мультиплікативним трендом

Метод нормованого розмаху (R/S-аналіз) [29]. Застосування методу передбачає такі кроки:

Крок 1. Визначають розмах:

, (1.3.20)

де R — розмах відхилення Y;

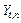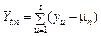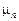— нагромадження відхилення за п періодів, , — рівень ряду в році и; — середнє за 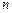періодів;

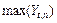— максимальне значення Y;

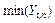— мінімальне значення для Y;

Крок 2. Для різних часових періодів обчислюють — 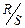, де — відповідне нормованому розмаху середньоквадратичне відхилення.

Нормована величина розмаху функціонально пов’язана з 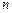таким чином:

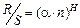, (1.3.21)

де 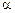— константа; — показник Херста.

Крок 3. Оцінюється показник Херста як коефіцієнт регресії, рівняння якої виходить після логарифмування співвідношення (1.3.21):

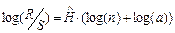. (1.3.22)

Ця оцінка не має жодного припущення щодо розподілу випадкової величини.

За значенням показника Херста можна дійти таких висновків:

1) Якщо 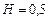— економічний процес являє собою випадкове блукання, а розмах нагромаджених відхилень має збільшуватися пропорційно квадратному кореню від часу п.

2) 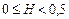. Цей діапазон відповідає ергодичним антиперсистентним рядам. Такий тип процесу часто називають «поверненням до середнього».

Антиперсистентний часовий ряд єбільш мінливим, ніж ряд випадковий, оскільки складається з частих реверсів «спад-під­йом». Якщо процес демонструє зростання в попередньому періоді, то в наступному періоді найімовірніше почнеться спад. І навпаки, якщо відбувався спад, то ймовірний близький підйом. Стійкість такої поведінки залежить від того, наскільки H близьке до нуля. Чим ближче його значення до нуля, тим більше значення коефіцієнта від’ємної автокореляції рівнів часового ряду. Незважаючи на поширення концепції повернення до середнього в економічній та фінансовій літературі, досі було знайдено мало таких рядів.

3) За 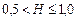маємо персистентні, або тренд-стійкі ряди. Якщо ряд зростає (спадає) у попередній період, то він імовірно буде зберігати цю тенденцію певний час у майбутньому. Тренди очевидні. Трендо-стійкість поведінки, або сила персистентності, збільшується мірою наближення до одиниці, або 100 % автокореляції. Чим ближче до 0,5, тим більше ряд зазнає впливу шуму і тим менш виражений його тренд.

Персистентний ряд — це узагальнений броунівський рух, або випадкові блукання із дрейфом. Сила зсуву залежить від того, наскільки Н перевищує 0,5. Такі ряди є нестабільними, вони влас­тиві ринкам капіталу. Персистентний часовий ряд має довготривалу пам’ять, тому в ньому спостерігаються довготермінові кореляції між поточними подіями й подіями майбутніми.

Коли Н відрізняється від 0,50, це означає, що спостереження не є незалежними. Кожне спостереження несе пам’ять про всі минулі події. Це не короткотривала пам’ять, яку часто називають «марківською». Це інша пам’ять — довготривала, теоретично вона зберігається назавжди. Тобто нещодавні події справляють силь­ніший вплив, ніж події віддалені, але залишковий вплив останніх завжди відчутний. цієї умови відображає нелінійність динамічного процесу.

Дата добавления: 2014-11-08