Модели систем с одной степенью свободы в частотной области

Модели систем с одной степенью свободы

Так как каждый пик (или мода) характеристики конструк­ции может быть представлен при помощи модели системы с одной степенью свободы, мы рассмотрим некоторые ас­пекты динамики систем с одной степенью свободы. В част­ности, мы исследуем методы построения моделей системы с одной степенью свободы в физической, временной и частот­ной областях. Эти модели не предназначены для представле­ния физических конструкций, но они служат в качестве инструмента для интерпретации их динамического пове­дения (представленного с помощью набора предположений и граничных условий). Модели оказываются полезными для:

- понимания и интерпретации динамического поведения конструкции

- описания динамических свойств конструкции с помощью небольшого набора параметров

- определения динамических параметров на основе экспе­риментальных результатов (подбор кривой).

Аналитическая модель может быть построена в физиче­ской области. Она представляет собой абстрактную систему, состоящую из точечной массы (m), опирающуюся на бези­нерционную линейную пружину (k) и связанную с вязкост­ным демпфером (с). Масса установлена таким образом, что она может перемещаться только в одном направлении (х), т.е. система имеет одну степень свободы.

Математическая модель во временной области может быть получена путем приложения второго закона Ньютона к аналитической модели. Приравнивая внутренние силы (инерции, затухания и упругости) и внешние силы (возбу­ждения), мы получим следующую модель:

mx(t) + cx(t) + kx(t) = f(t) (1)

Эта модель представлена в виде дифференциального уравне­ния второго порядка. Более простая в математическом отно­шении модель может быть получена в частотной области.

Модель с пространственными параметрами может быть построена в частотной области для описания частотной ха­рактеристики Н(ω) в терминах массы, жесткости и коэффи­циента затухания.

Давайте рассмотрим поведение этой модели под воздейст­вием синусоидального возбуждения и проследим за измене­ниями модуля | Н(ω) | и фазы Н(ω) при изменении часто­ты.

Статическое смещение определяется только жесткостью пру­жины. При низких частотах реакция, определяемая в основ­ном пружиной, находится в фазе с силой возбуждения.

При увеличении частоты присущая массе сила инерции оказывает возрастающее влияние. При определенной частоте ( - собственная частота незатухающих колебании) соответствующие массе и пружине составляющие взаимно аннулируются и реакция определяется только присущей демпферу составляющей. Следовательно, податливость си­стемы увеличивается. Если присущая демпферу составля­ющая была бы равна нулю, то податливость стала бы беско­нечной. При частоте 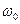реакция отстает от силы возбуждения на 90°.

При частотах, превышающих 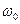, основное влияние оказы­вает присущая массе составляющая и система начинает вести себя как чистая масса, податливость уменьшается, а реакция отстает от силы возбуждения на 180°.

Модель частотной характеристики является безпараметрической. Она основана на определяющем Н(ω) выражении, т.е.

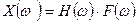(2)

Функция Н(ω) является частотной характеристикой податли­вости (перемещение/сила). Она представляет собой отноше­ние выходного и входного спектров и изменяется в зависи­мости от частоты (ω).

Эта модель связывает аналитическую модель системы с од­ной степенью свободы с практическими измерениями и их результатами.

Модель с пространственными параметрами (см. рис.2) является идеаль­ной для работы с аналитическими системами. Обычно нам неизвестны распределения массы, жесткости и затухания реальных конструкций. Следующая модель представляет со­бой практическую связь между теорией и практикой.

Модель с модальными параметрами показана на рис.3. Она построена с помощью двух параметров, которые могут быть получены по результатам измерения частотных хара­ктеристик.

На рис.3 функция Н(ω) определяется координатой полюса (р) и вычетом (R) и их комплексно сопряженными величинами (р* и R*). Координата полюса и вычет в свою очередь определяются через пространственные параметры.

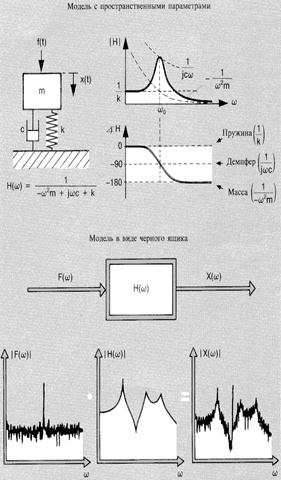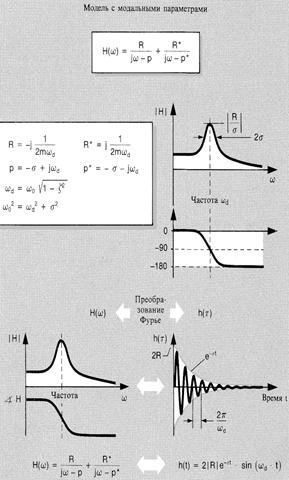Рис. 2. Модель с пространственными параметрами

Рис. 3. Модель с модальными параметрами

Координата полюса представляет собой комплексную величи­ну. Численное значение ее действительной части (σ) пред­ставляет собой скорость затухания колебаний. Это показано на графике зависимости импульсной характеристики от вре­мени. В частотной области, а представляет собой половину ширины полосы (-3 дБ) пика частотной характеристики. Мнимая часть координаты полюса представляет собой мо­дальную частоту - собственную частоту свободно затуха­ющих колебаний (ωd).

Вычет в случае системы с одной степенью свободы пред­ставляет собой мнимую величину, которая отображает ин­тенсивность моды колебаний.

Как показано на рис.3, координата полюса и вычет могут быть экспериментальным путем на основе измеренной и из­ображаемой на экране анализатора частотной характеристи­ки. Таким образом, модель с модальными параметрами дает связь аналитических моделей с результатами эксперимен­тальных исследований.

Дата добавления: 2014-11-18