Степени свободы и модели систем с несколькими степенями свободы

Предыдущие модели относились к случаю одной степени свободы, т.е. к перемещению в одном направлении. Реаль­ные конструкции имеют много точек, которые могут переме­щаться независимо друг от друга, т.е. они являются систе­мами с несколькими степенями свободы. Для определения частотной характеристики реальной конструкции необходи­мо замерить силу возбуждения и реакцию в двух точках. Однако, каждая точка может перемещаться максимально в шести возможных направлениях и поэтому необходимо так­же определить направление перемещения.

Степень свободы (СС) представляет собой определенную точку и направление ее перемещения. Индекс i используется для указания степени свободы реакции, а индекс j - для сте­пени свободы возбуждения. Дополнительные индексы х, у и z могут быть использованы для указания направления. Таким образом:

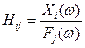(3)

Написав функцию Н_ij(ω) двумя способами, можно получить две модели систем с несколькими степенями свободы. Эти модели описаны уравнениями на рисунке.

Модель системы с несколькими степенями свободы, осно­ванная на частотных характеристиках, представляет фун­кцию Н_ij(ω) как сумму частотных характеристик систем с одной степенью свободы, по одной функции для каждой моды в пределах учитываемого частотного диапазона, при­чем r - порядковый номер моды, am- число мод в модели.

Модель системы с несколькими степенями свободы, ос­нованная на модальных параметрах, определяет функцию Н_ij(ω) в терминах координат полюсов и присущих отдель­ным модам вычетов. Эта модель указывает на два важных свойства модальных параметров:

- модальная частота и затухание являются глобальными параметрами. Координата полюса имеет только модаль­ный номер (r) и не зависит от учитываемой степени свободы;

- вычет является локальным параметром. Индекс (ij) свя­зывает вычет с конкретной комбинацией степеней свобо­ды и конкретной модой.

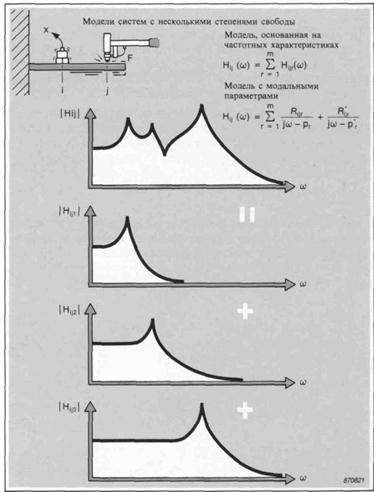
Рис.4. Модель с несколькими степенями свободы.

Дата добавления: 2014-11-18