Взаимность

Однородность

Наложение

Линейность

Предположения модального описания

Сильно связанные моды — сложные конструкции

Частотные характеристики конструкций с сильным затуха­нием или высокой модальной плотностью не указывают на четко разделенные моды. При этом говорят, что моды сильно связаны, а реакция при любой частоте представляет собой комбинацию многих мод. Сложные конструкции мо­гут быть все-таки описаны с помощью дискретного набора мод, но методы, необходимые для определения модальных параметров, более сложные.

В пункте 1.10 были рассмотрены понятия высо­кой модальной плотности и сильного затухания. Но ни один из этих двух факторов не мешает применению к кон­струкции модального описания. Они только усложняют ис­пользуемые методы.

Лишь одно предположение необходимо сделать - предполо­жение о линейности.

Необходимо предположить, что исследуемые системы имеют линейные свойства, т.е. что реакция всегда пропорциональна силе возбуждения. Это предположение имеет три следствия для измерений частотных характеристик.

Измеряемые частотные характеристики не зависят от типа и формы волны возбуждения. Возбужде­ние синусоидальной силой с разверткой частоты дает те же результаты, что и возбуждение широкополосной слу­чайной силой.

Измеряемые частотные характеристики не зависят от уровня возбуждения.

В линейной механической системе существу­ет частная симметрия, которая описывается теоремой взаимности Максвелла. Отсюда следует, что измеряемые частотные характеристики не зависят от того, какая точка используется для возбуждения, а какая - для изме­рения реакции.

2. ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ «ТОПЛИВО-КОРПУС» - «КОРПУС – ТОПЛИВО»

В соответствии с определением – передаточная функция это отношение выходного сигнала к входному сигналу.

	Н(ω)

Хi (t) Yi (t)

Рис. 7

Н(ω)= Yi (t)/ Хi (t) (6)

Передаточная функция при проведении модального анализа строится во всем частотном диапазоне объекта и будет определяться спектральной плотностью ее распределения. Характер спектрального распределения не будет зависеть от объекта, если его характеристики являются постоянными. При наличии большого количества элементов объекта, существенную роль в изменении характеристики спектральной плотности передаточной функции будут играть границы и зоны нагружения импульсной нагрузкой исследуемые элементы объекта. Это существенно при проведении диагностирования объекта – знание влияния перехода или границы контактной зоны.

При рассмотрении передаточной функции «корпус - топливо» и «топливо- корпус» исследовательский процесс строится в частотном диапазоне собственных частот топлива и корпуса.

2.1. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ИМПУЛЬСНОГО ВОЗДЕЙСТВИЯ

При проведении модального анализа в качестве возбуждающего сигнала используется импульс, т.к. для твердых (а при некоторых условиях, и в жидких и газообразных) объектов свойственно преобразование в собственные гармонические затухающие колебания. При этом параметры отклика на импульсное воздействие определяются двумя взаимно независимыми факторами - свойствами возбуждаемых импульсным воздействием колебательных систем и параметрами самого импульсного воздействия.

Важнейшей импульсной функцией при рассмотрении спектрально-временных преобразований является дельта (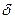) – функция – сигнал прямоугольной формы, длительности и амплитудой (рис. 8) при следующем условии:

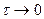при . (7)

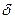- функция имеет бесконечно большую величину амплитуды при бесконечно малом значении длительности. Сразу оговоримся, что 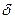- функция является математической абстракцией, не реализуемой на практике. Создание воздействия с амплитудой, равной бесконечности, энергетически невозможно, а при стремлении к ней вызвало бы разрушение объекта исследования. Но с информативных позиций значение 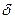- функции очень велико.

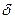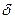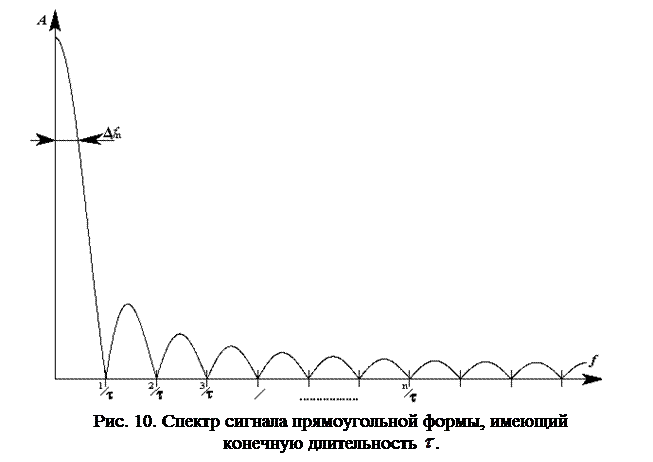
Спектральное изображение - функции показано на рис. 9 и представляет собой горизонтальную линию . В сигнале содержатся составляющие, имеющие абсолютно все частоты и все фазовые соотношения между этими составляющими. Формально математически это действительно так, но для восприятия физического смысла спектрального изображения - функции представляется удобным другой подход. Постоянство плотности спектра во всем частотном диапазоне свидетельствует о том, что подобного рода сигнал с одинаковой эффективностью возбудил бы колебательную систему с любой собственной частотой. Сигнал прямоугольной формы, имеющий конечную длительность , имеет спектр, подобный показанному на рис. 10. Такой сигнал может возбудить колебательные системы, имеющие различные частоты, далеко не с одинаковой эффективностью, и эффективность эта падает с частотой тем быстрее, чем больше длительность импульса . Если интересующий нас диапазон частот не превышает 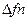(рис.10), при том, что плотность спектра прямоугольного импульса в этом диапазоне изменяется в допустимых пределах, мы имеем право относиться к такому импульсному воздействию как к 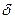- функции. При анализе результата импульсного возбуждения колебательной системы мы в этом случае можем не учитывать параметры воздействия, считая его бесконечно коротким независимо от действительного значения . Смысл того, что спектр прямоугольного импульса на частотах, равных величинам (где - любое целое число), обращается в нуль, станет понятным из следующего рассуждения. Если объектом воздействия является колебательная система, собственная частота которой равна 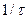, то получается, что если фронт прямоугольного импульса эту систему возбуждает, то спад его (задний фронт) через время, равное периоду этой частоты, воздействует на эту же колебательную систему в противофазе, в результате чего возникшие было колебания прекратятся. То есть при 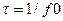колебательная система данным прямоугольным импульсом возбуждена не будет. Этот эффект легко наблюдать при возбуждении прямоугольным электрическим импульсом единичного L-C контура с сосредоточенными параметрами.

В отличие от электрического, акустическое воздействие в виде прямоугольного импульса осуществить крайне сложно. Даже, более того, обычно не представляется возможным выяснить истинную форму импульсного воздействия. Однако независимо от формы импульса увеличение длительности ударного взаимодействия сопровождается уменьшением полосы частот , в которой этот импульс может достаточно эффективно возбудить колебательную систему. При этом спектр импульсного воздействия, не имеющего крутых фронтов, нигде не имеет значения, равного нулю. Соотношение между и на уровне, достаточном для качественной оценки возможностей импульсного воздействия выглядит следующим образом:

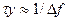. (8)

Строго говоря, любое импульсное воздействие имеет бесконечный спектр. Выражение же (8) характеризует ту полосу частот , в которой возбуждение некоторой колебательной системы с помощью импульса заданной длительности энергетически целесообразно. За пределами этой полосы амплитуда колебаний возбуждаемой колебательной системы будет незначительной.

Сила, действующая на единицу площади поперечного сечения, называется напряжением:

(9)

Английский физик Р. Гук экспериментально установил, что для малых деформаций относительное удлинение (перемещение) 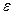и напряжение 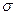прямо пропорциональны друг другу:

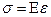(10)

где коэффициент пропорциональности 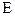называется модулем Юнга.

Из формул (9) и (10) вытекает, что

(11)

Второй закон Ньютона – основной закон динамики поступательного движения – отвечает на вопрос, как изменяется механическое движение тела под действием приложенных к нему сил:

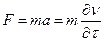(12)

Из формул и вытекает, что

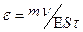(13)

Для определения амплитуды ускорения:

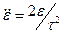(14)

Изменение амплитуды описывается формулой:

(15)

Дата добавления: 2014-11-18