Транспортных задач

Как уже отмечалось ранее, математическая модель транспортной задачи имеет ряд особенностей:

1) все ограничения представлены уравнениями;

2) коэффициенты при неизвестных в ограничениях равны либо 0, либо 1.

Поэтому данные особенности позволили преобразовать симплекс-метод в метод потенциалов, и тем самым существенно упростить решение транспортной задачи. Таким образом, найденное исходное опорное решение (методом min элемента либо методом северо-западного угла) проверяется на оптимальность методом потенциалов по следующему критерию: если опорное решение транспортной задачи является оптимальным, то ему соответствует система m + n действительных чисел U_i и V_j, удовлетворяющих условиям:

1. U_i + V_j = C_ij – для всех заполненных клеток x_ij;

2. U_i + V_j ≤ C_ij – для свободных клеток.

Числа U_i и V_j называются потенциалами. В распределительную таблицу добавляют строку V_j и столбец U_i.

Выбираем из двух опорных решений то, которое имеет минимальные затраты, т.е. метод min элемента и проверим его на оптимальность, добавив в распределительную таблицу строку V_j и столбец U_i.

Ai Bj		B1	B2	B3
	Vj Ui		+3
A1		30 ^2 −	^5	60 ^2 + 90
A2	-2	30 ^4 +	^1	100 ^5 − 70
A3		110 ^3 +	^6	0 ^8 −

Составим систему для заполненных клеток по критерию :

5 уравнений, 6 неизвестных.

Одному из потенциалов дается произвольное значение, например, полагаем U₁ = 0.

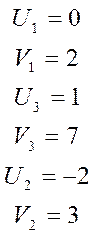
Найденные значения потенциалов заносим в таблицу и проверяем потенциальность незаполненных клеток по критерию: U_i – V_j ≤ C_ij

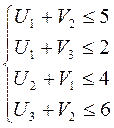
Так как одна клетка оказалась не потенциальной, то данное опорное решение не является оптимальным и его можно улучшить.

Дата добавления: 2014-11-08