Устно). Рассмотрим матричную игру следующего вида

Ui	V1	V2	V3	V4	V5
U1
U2
U3
U4

Где U_i – стратегии игрока 1 и соответствующий выигрыш, а V_j – стратегии игрока 2 и соответствующий проигрыш (т.к. в парной игре выигрыш одного влечет за собой проигрыш другого).

Игроку 1 предпочтительнее выбрать стратегию с наибольшим выигрышем, поэтому он, очевидно, выберет стратегию U₃. Однако, у игрока 2 имеется выбор из пяти стратегий, поэтому он может воспользоваться стратегией V₃, и тогда выигрыш игрока 1 окажется минимальным (1). Аналогичные ситуации возможны и при использовании игроком 1 других стратегий. Вместе с тем, минимальные значения выигрыша для различных стратегий игрока 1 различны между собой. В этой связи для него имеет смысл выбрать такую стратегию U_i, для которой минимальный выигрыш будет наибольшим на множестве остальных стратегий.

Подобный подход к решению рассматриваемой задачи называют принципом гарантированного результата. Выбранную с его использованием стратегию называют максиминной, а полученный в результате её применения выигрыш называют максиминным, или нижней ценой игры.

т.е. находится

(1)

Определение. Число 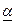, определённое по формуле (1) называется нижней чистой иеной игры и показывает, какой минимальный выигрыш может гарантировать себе игрок 1, применяя свои чистые стратегии при всевозможных действиях игрока 2, поэтому для нашего примера:

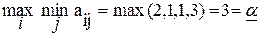
Аналогичные рассуждения можно провести для игрока 2, который при оптимальном своём поведении должен стремится по возможности за счёт своих стратегий максимально уменьшить выигрыш игрока 1. Поэтому для игрока 2 отыскива­ется

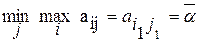(2)

Поэтому, для нашего примера:

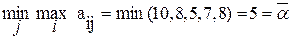
Определение. Число , определяемое по формуле (2), называется чистой верхней ценой игры и показывает, какой максимальный выигрыш за счёт своих стратегий может себе гаран­тировать игрок 1.

Вывод: применяя свои чистые стратегии, игрок 1 может обеспечить себе выиг­рыш не меньше 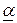, а игрок 2 за счёт применения своих чистых стратегий может не допустить выигрыш игрока 1 больше, чем .

Максиминные стратегии игроков становятся устойчивыми, пока оба игрока их придерживаются и выигрыш одного из них равен проигрышу другого (т.е. нет места риску). Такая игра с матрицей A, где , то говорят, что эта игра имеет седловую точку в чистых стратегиях и чистую иену игры

Седловая точка - это пара чистых стратегий (i₀, j₀) соответственно игроков 1 и 2, при которых достигается равенство .

В это понятие вложен следующий смысл: если один из игроков придерживается стратегии, соответствующей седловой точке, то другой игрок не смо­жет поступить лучше, чем придерживаться стратегии, соответствующей седловой точке. Мате­матически это можно записать и иначе:

§2. СМЕШАННОЕ РАСШИРЕНИЕ МАТРИЧНОЙ ИГРЫ.

Исследование в матричных играх начинается с нахождения её седловой точки в чистых стратегиях. Если матричная игра имеет седловую точку в чистых стратегиях, то нахождением этой седловой точки заканчивается исследование игры.

Если же в игре нет седловой точки в чистых стратегиях, то можно найти нижнюю и верхнюю чистые цены этой игры, которые ука­зывают, что игрок 1 не должен надеяться на выигрыш больший, чем верхняя цена игры, и мо­жет быть уверен в получении выигрыша не меньше нижней цены игры. Улучшение решений матричных игр следует искать в использовании секретности применения чистых стратегий и возможности многократного повторения игр в виде партии. Этот результат достигается путём применения чистых стратегий случайно, с определённой вероятностью.

Определение. Смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий.

Таким образом, если игрок 1 имеет т чистых стратегий 1,2,...,т, то его смешанная стратегия х - это набор чисел х = (x₁,..., x_m) удовлетворяющих соотношениям

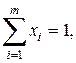
Аналогично для игрока 2, который имеет п чистых стратегий, смешанная стратегия у – это набор чисел

y = (y₁, …, y_n),

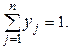
Так как каждый раз применение игроком одной чистой стратегии исключает применение дру­гой, то чистые стратегии являются несовместными событиями. Кроме того, они являются един­ственными возможными событиями.

Чистая стратегия есть частный случай смешанной стратегии. Действительно, если в сме­шанной стратегии какая-либо i-я чистая стратегия применяется с вероятностью 1, то все ос­тальные чистые стратегии не применяются. И эта i-я чистая стратегия является частным слу­чаем смешанной стратегии. Для соблюдения секретности каждый игрок применяет свои страте­гии независимо от выбора другого игрока.

Определение. Средний выигрыш игрока 1 в матричной игре с матрицей А выражается в виде математического ожидания его выигрышей

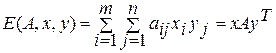
Первый игрок имеет целью за счёт изменения своих смешанных стратегий х максимально увеличить свой средний выигрыш Е (А, х, у), а второй - за счёт своих смешанных стратегий стремится сделать Е (А, х, у) минимальным, т.е. для решения игры необходимо найти такие х и у, при которых достигается верхняя цена игры

Аналогичной должна быть ситуация и для игрока 2, т.е. нижняя цена игры должна быть

Подобно играм, имеющим седловые точки в чистых стратегиях, вводится следующее оп­ределение: оптимальными смешанными стратегиями игроков 1 и 2 называются такие наборы х⁰, у⁰ соответственно, которые удовлетворяют равенству

Величина Е (А, х⁰, у⁰) называется при этом ценой игры и обозначается через .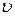

Имеется и другое определение оптимальных смешанных стратегий:, х⁰, у⁰ называются оп­тимальными смешанными стратегиями соответственно игроков 1 и 2, если они образуют седловую точку:

Оптимальные смешанные стратегии и цена игры называются решением матричной игры.

Основная теорема матричных игр имеет вид:

Теорема (о минимаксе). Для матричной игры с любой матрицей А величины

существуют и равны между собой.

§3. СВОЙСТВА РЕШЕНИЙ МАТРИЧНЫХ ИГР.

Обозначим через G {X, Y,A) игру двух лиц с нулевой суммой, в которой игрок 1 выбирает стратегию х X, игрок 2 - у Y, после чего игрок 1 получает выигрыш А = А (х, у) за счёт игрока 2.

Определение. Стратегия х¹ игрока 1 доминирует (строго доминирует) над стратегией х², если

A(x¹, y) ≥ A(x², y) (A(x¹, y) ≥ A(x², y)) y Y

Стратегия у¹ игрока 2 доминирует (строго доминирует) над стратегией

A(x, y¹) ≥ A(x, y²) (A(x, y²) ≥ A(x, y²)) x X

При этом стратегии х² и у² называются доминируемыми (строго доминируемыми).

Спектром смешанной стратегии игрока в конечной антагонистической игре называется множество всех его чистых стратегий, вероятность которых согласно этой стратегии положи­тельна.

Свойство 1. Если чистая стратегия одного из игроков содержится в спектре некоторой его оптимальной стратегии, то выигрыш этого игрока в ситуации, образованной данной чистой стратегией и любой оптимальной стратегией другого игрока, равен значению конечной антаго­нистической игры.

Свойство 2. Ни одна строго доминируемая чистая стратегия игрока не содержится в спектре его оптимальной стратегии.

Игра G' = (X', Y ',А') называется подыгрой игры G (X,Y,A), если X' X, Y' Y, а матрица А' является подматрицей матрицы А. Матрица А' при этом строится следующим образом. В матрице А остаются строки и столбцы, соответствующие стратегиям X' и Y', а остальные "вычер­киваются". Всё то что "останется" после этого в матрице А и будет матрицей А'.

Свойство 3. Пусть G = (X,Y,A) - конечная антагонистическая игра, G' = (X \ x',Y,A) - подыгра игры G, а. х' - чистая стратегия игрока 1 в игре G, доминируемая некоторой стратегией , спектр которой не содержит х'. Тогда всякое решение (х⁰, у⁰, 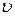) игры G' является решением игры G.

Свойство 4. Пусть G = (X,Y,A) - конечная антагонистическая игра, G' = (X,Y \у',А) - подыгра игры G, а, у'- чистая стратегия игрока 2 в игре G, доминируемая некоторой стратегией , спектр которой не содержите Тогда всякое решение игры G' является решением G.

Свойство 5. Если для чистой стратегии х' игрока 1 выполнены условия свойства 3, а для чистой стратегии у ' игрока 2 выполнены условия свойства 4, то всякое решение игры G' = (X \ x'.Y \ у', А) является решением игры G = (X,Y,A).

Свойство б. Тройка (х⁰, у⁰, 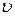) является решением игры G = (X,Y,A) тогда и только тогда, когда (х⁰, у⁰, k 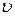+a) является решением игры С(Х, У, кА+а), где а - любое вещественное число, к>0.

Свойство 7. Для того, чтобы х⁰ = (х₁⁰,...,х_i⁰,..., х_m⁰) была оптимальной смешанной стратегией матричной игры с матрицей А и ценой игры 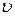, необходимо и достаточно выполне­ние следующих неравенств

(*)

Аналогично для игрока 2: чтобы y ⁰ = (y₁⁰,...,y_j⁰,..., y_n⁰) была оптимальной смешанной стратегией игрока 2 необходимо и достаточно выполнение следующих неравенств:

(**)

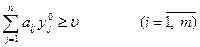Из последнего свойства вытекает: чтобы установить, является ли предполагаемые (х, у) и 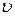ре­шением матричной игры, достаточно проверить, удовлетворяют ли они неравенствам (*) и (**). С другой стороны, найдя неотрицательные решения неравенств (*) и (**) совместно со следую­щими уравнениями

(***)

получим решение матричной игры.

Таким образом, решение матричной игры сводится к нахождению неотрицательных па­раметров решений линейных неравенств (*) (**) и линейных уравнений (***). Однако это тре­бует большого объёма вычислений, которое растёт с увеличением числа чистых стратегий иг­роков. (Например для матрицы 3х3 имеем систему из 6 неравенств и 2 уравнений). Поэтому в первую очередь следует, по возможности используя свойства 2 и 3, уменьшить число чистых стратегий игроков. Затем следует во всех случаях проверить выполнение неравенства

Если оно выполняется, то игроки имеют чистые оптимальные стратегии (игрок 1 - чис­тую максиминная, а игрок 2 - чистую минимаксная). В противном случае хотя бы у одного иг­рока оптимальные стратегии будут смешанные. Для матричных игр небольшого размера эти решения можно найти, применяя свойства 1-5.

Замечание. Отметим, что исключение доминируемых (не строго) стратегий может при­вести к потере некоторых решений. Если же исключаются только строго доминируемые страте­гии, то множество решений игры не изменится.

Пример 3. Пусть G = (X,Y,A), где Х= {1, 2, 3, 4}; Y= {1, 2, 3, 4}, а функция выигрыша А задана следующим образом:

1 2 3 4

Решение. Прежде всего заметим, что по свойству 6 достаточно решить игру G¹ = (X, Y, A), где 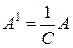. В матричной форме игра G¹ определяется матрицей выигрышей

1 2 3 4

Элементы четвертой строки этой матрицы «≤» соответствующих элементов третьей строки и поэтому третья стратегия игрока 1 доминирует над четвертой. Кроме того, элементы первого столбца матрицы А¹ «≥» соответствующих элементов второго столбца. Следовательно, вторая стратегия игрока 2 доминирует над его первой стратегией.

Далее, из свойства 5 следует, что всякое решение игры G² = (X / {4}, Y / {1}, A¹) является решением игры G¹. В матричной форме игру G² можно представить матрицей

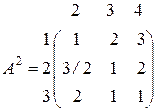
Очевидно, что элементы второй строки «≥» полусуммы соответствующих элементов первой и третьей строк. Кроме того, элементы третьего столбца матрицы А² «≥» соответствующих элементов второго столбца. Применяя свойство 5 получим, что всякое решение игры G³ = (X / {4,2}, Y / {1,4} A²) является решением игры G², а следовательно и игры G¹. Игра G³ определяется матрицей

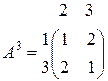
Матрица А³ не имеет седловой точки, т.к. выполнено равенство

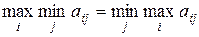
а игра G³ не имеет решения в чистых стратегиях, т.е. оптимальные стратегии игроков являются смешанными. Эти стратегии (в данном случае) легко найти из анализа структуры матрицы А³. поскольку матрица А³ симметрична, можно предположить, что игроки в оптимальной стратегии используют свои чистые стратегии равными вероятностями.

Действительно, если игрок 1 выбирает с равными вероятностями стратегии 1 и 3, то при применении любой из двух чистых стратегий игроком 2 математическое ожидание выигрыша игрока 1 будет равно либо

,

либо

.

Аналогично, если игрок 2 использует свои чистые стратегии 2 и 3 с равными вероятностями, то математическое ожидание его проигрыша будет равно . Следовательно, указанные стратегии являются оптимальными в игре G³, а величины - значением игры G³. Из предыдущего сле­дует, что эти стратегии оптимальны и в G¹.

Таким образом, стратегия Х = () является оптимальной стратегией игрока 1, стратегия Y = () - оптимальной стратегией игрока 2 в игре G¹, а значение игры G¹ равно . В силу свойства 4 решением игры G будет тройка (X, Y, ).

Дата добавления: 2014-11-08