Графический метод решения игр 2 Х n и m Х 2

Поясним метод на примерах.

Пример 1. Рассмотрим игру, заданную платёжной матрицей.

На плоскостихОу введём систему координат и на осиОх отложим отрезок единичной длины A₁, А₂, каждой точке которого поставим в соответствие некоторую смешанную страте­гию игрока 1 (х, 1 - х). В частности, точке A₁ (0;0) отвечает стратегия A₁, точке А₂ (1;0) - стра­тегия А₂ и т.д.

В точках A₁ и А₂ восстановим перпендикуляр и на полученных прямых будем отклады­вать выигрыш игроков. На первом перпендикуляре (в данном случае он совпадает с осью Оу) отложим выигрыш игрока 1 при стратегии A₁, а на втором - при стратегии A₂. Если игрок 1 применит стратегию A₁, то выиграет при стратегии B₁ игрока 2-2, при стратегии В₂ - 3, а при стратегии В₃ - 11. Числам 2, 3, 11 на оси Ox соответствуют точки B₁, B₂, B₃

Если же игрок 1 применит стратегию А₂, то его выигрыш при стратегии B₁ равен 7, при В₂ - 5, а приВ₃ - 2. Эти числа определяют точки B’₁, B’₂, B’₃ на перпендикуляре, восстановлен­ном в точке А₂. Соединяя между собой точки B₁ и B’₁, B₂ и B’₂, B₃ и B’₃ и получим три прямые, расстояние до которых от оси Ох определяет средний выигрыш при любом сочетании соответ­ствующих стратегий. Например, расстояние от любой точки отрезка B₁B’₁ до оси 0х определяет средний выигрыш υ₁ при любом сочетании стратегий A₁A₂ (с частотами х и 1-х) и стратеги­ей В₁игрока 2. Это расстояние равно

2х₁ +6 (1 – х₂) = υ₁

(Вспомните планиметрию и рассмотрите трапецию А₁В₁В`₁А₂). Таким образом, ординаты то­чек, принадлежащих ломанной В₁ М N B’₃ определяют минимальный выигрыш игрока 1 при применении им любых смешанных стратегий. Эта минимальная величина является максималь­ной в точке N; следовательно этой точке соответствует оптимальная стратегия X* = (х, 1-х), а её ордината равна цене игры υ. Координаты точки N находим как точку пересечения прямых B₂B’₂ и B₃B’₃

Соответствующие два уравнения имеют вид

Þ .

Следовательно , при цене игры 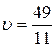. Таким образом, мы можем найти оптимальную стратегию при помощи матрицы

Дата добавления: 2014-11-08