Получаем новый цикл

Решения к другому.

Переход от одного опорного

Улучшают план, составляя цикл с одной из не потенциальных клеток, причем эта не потенциальная клетка должна являться одной из вершин цикла, а остальные вершины должны обязательно соответствовать перевозкам.

Цикл перераспределения ресурсов составляют по следующим правилам:

1. Этот цикл представляет собой замкнутый многоугольник с вершинами в загруженных клетках (за исключением вершины, которая является не потенциальной клеткой), и звеньями, лежащими вдоль строк и столбцов матрицы.

2. Ломанная линия должна быть связанной в том смысле, что из любой её вершины можно попасть в любую другую вершину по строке или столбцу.

3. В каждой вершине цикла встречаются только два звена, одно из них располагается по строке, другое – по столбцу.

4. Число вершин цикла чётное, все они в процессе перераспределения делятся на загружаемые и разгружаемые.

5. В каждой строке (столбце) имеются две вершины: одна загружаемая, другая – разгружаемая.

Таким образом, строим цикл для не потенциальной клетки (1;3). У вершин цикла ставим знаки (+) и (−) и записываем грузы. У вершин со знаком (−) выбираем минимальный груз, он равен 60. Его прибавляем к грузам, стоящим у положительных вершин, и вычитаем из грузов, стоящих у отрицательных вершин.

Снова проверим полученное решение на оптимальность:

2.

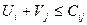
Таким образом, клетка (2;1) не потенциальна. Получение нового плана осуществляется в том же порядке, что и предыдущий, т.е. строим с ней цикл, и проверяем полученный план на оптимальность аналогично.

		В1	В2	В3	Запасы
	V i Ui		-2
А1		-				+
0 30	-	90 60
А2		+				-
30 -		70 100
А3
	-
Потребности

Все свободные клетки оказываются потенциальными, следовательно, последний план оптимальный:

		В1	В2	В3	Запасы
	V i Ui		-2
А1
	-
А2
А3
	-
Потребности

усл. ед.

Таким образом, построением начального плана и последующим расчетом двух итераций (циклов) получено оптимальное решение по прикреплению пунктов отправления грузов к пунктам назначения.

Тема: Теория игр.

В экономике иногда приходится сталкиваться с ситуацией, когда при наличии многих участников эффективность решения одного из них зависит от того, какие решения приняли другие участники. Например, доход предприятия от продажи изделия зависит не только от установленной на него цены, но и от количества купленных покупателем изделий. Или при выборе ассортимента товаров, выпускаемых предприятием, нужно учитывать, какой ассортимент товаров выпускают другие предприятия.

Все ситуации, когда эффективность действия одного из участников зависит от действий других, можно разбить на два типа:

· Интересы участников совпадают, и они могут договориться о совместных действиях. Если в качестве противоположности выступает неактивная, пассивная сторона, которая явно активно не противодействует достижению намеченной цели, то такие игры называются играми с «природой». В качестве такой стороны в коммерции является неизвестность поведения клиентов, реакция населения на новые виды товаров, неясность погодных условий при перевозке товаров или проведении ярмарки и т.п.

· Интересы участников не совпадают. В этом случае может оказаться не выгодным сообщать другим участникам свои решения, т.к. кто-нибудь из них сможет воспользоваться знанием чужих решений и получит больший выигрыш за счет других участников. Ситуации такого типа называются конфликтными.

Построением математических моделей конфликтных ситуаций и разработкой методов решения, возникающих в этих ситуациях задач, занимается ТЕОРИЯ ИГР.

§1. КЛАССИФИКАЦИЯ ИГР.

Классификацию игр можно проводить: по количеству игроков, количеству стратегий, ха­рактеру взаимодействия игроков, характеру выигрыша, количеству ходов, состоянию информа­ции и т.д.

В зависимости от количества игроков различают игры двух и п игроков. Первые из них наиболее изучены. Игры трёх и более игроков менее исследованы из-за возникающих принци­пиальных трудностей. Чем больше игроков - тем больше проблем.

По количеству стратегий игры делятся на конечные и бесконечные. Если в игре все игро­ки имеют конечное число возможных стратегий, то она называется конечной. Если же хотя бы один из игроков имеет бесконечное количество возможных стратегий игра называется беско­нечной.

По характеру взаимодействия игры делятся на:

1) бескоалиционные: игроки не имеют права вступать в соглашения, образовывать коа­лиции;

2) коалиционные (кооперативные) - могут вступать в коалиции.

3) в кооперативных играх коалиции наперёд определены.

По характеру выигрышей игры делятся на:

игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю) и игры с ненулевой суммой.

По виду функций выигрыша игры делятся на:

матричные, биматричные, непрерывные, выпуклые, сепарабельные, типа дуэлей и др.

Матричная игра - это конечная игра двух игроков с нулевой суммой, в которой задаётся выигрыш игрока 1 в виде матрицы (строка матрицы соответствует номеру применяемой стра­тегии игрока 1, столбец - номеру применяемой стратегии игрока 2; на пересечении строки и столбца матрицы находится выигрыш игрока 1, соответствующий применяемым стратегиям).

Для матричных игр доказано, что любая из них имеет решение и оно может быть легко найдено путём сведения игры к задаче линейного программирования.

Биматричная игра - это конечная игра двух игроков с ненулевой суммой, в которой вы­игрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец - стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице - выиг­рыш игрока 2.)

Для биматричных игр также разработана теория оптимального поведения игроков, одна­ко решать такие игры сложнее, чем обычные матричные.

Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной в зависимости от стратегий. Доказано, что игры этого класса имеют решения, однако не разработано практически приемлемых методов их нахождения.

Стратегией игрока называется совокупность правил, определяющих выбор варианта действий при каждом личном ходе этого игрока в зависимости от ситуации, сложившейся в процессе игры.

Оптимальной стратегией игрока называется такая стратегия, которая при многократном повторении игры, обеспечивает игроку максимально возможный средний выигрыш (минимально возможный средний проигрыш). Очевидно, выбирая ту или иную стратегию, каждый из игроков стремится удовлетворить свои интересы: первый – обеспечить себе максимально возможный выигрыш, а второй – минимально возможный проигрыш. Стратегия первого игрока называется оптимальной, если при её применении выигрыш первого игрока не может быть уменьшен, какими бы стратегиями ни пользовался второй игрок. Стратегия второго игрока является оптимальной в том случае, если проигрыш второго игрока не может быть увеличен, какими бы стратегиями ни пользовался первый игрок.

Основными вопросами теории игр, которые возникают в коммерческой деятельности, являются:

Ø В чем состоит оптимальность поведения каждого из игроков в игре, какие свойства стратегий следует считать признаками оптимальности;

Ø Существуют ли стратегии игроков, которые обладали бы атрибутами оптимальности;

Ø Если существуют оптимальные стратегии, то как их найти?

ГЛАВА 1. МАТРИЧНЫЕ ИГРЫ.

§1. РЕШЕНИЕ МАТРИЧНЫХ ИГР В ЧИСТЫХ СТРАТЕГИЯХ.

Матричная игра двух игроков с нулевой суммой может рассматриваться как следующая абстрактная игра двух игроков.

Первый игрок имеет т стратегий i = 1,2,...,т, второй имеет п стратегий j= 1,2,..., п. Каждой паре стратегий (i, j) поставлено в соответствие число a_ij, выражающее выигрыш игрока 1 за счёт игрока 2, если первый игрок примет свою i-ю стратегию, а 2 – свою j-ю стратегию.

Каждый из игроков делает один ход: игрок 1 выбирает свою i-ю стратегию (), 2 – свою j-ю стратегию (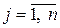 ), после чего игрок 1 получает выигрыш a_ij за счёт игрока 2 (если a_ij < 0, то это значит, что игрок 1 платит второму сумму | a_ij |. На этом игра заканчивается.

Дата добавления: 2014-11-08