Замены оборудования

П.1. Оптимальная стратегия

Некоторые экономические задачи, решаемые методами динамического программирования

Одной из важных экономических проблем является опреде­ление оптимальной стратегии в замене старых станков, агре­гатов, машин на новые.

Старение оборудования включает его физический и мораль­ный износ, в результате чего растут производственные затра­ты по выпуску продукции на старом оборудовании, увеличива­ются затраты на его ремонт и обслуживание, снижаются про­изводительность и ликвидная стоимость.

Наступает время, когда старое оборудование выгоднее про­дать, заменить новым, чем эксплуатировать ценой больших за­трат; причем его можно заменить новым оборудованием того же вида или новым, более совершенным.

Оптимальная стратегия замены оборудования состоит в определении оптимальных сроков замены. Критерием опти­мальности при этом может служить прибыль от эксплуата­ции оборудования, которую следует оптимизировать, или сум­марные затраты на эксплуатацию в течение рассматриваемого промежутка времени, подлежащие минимизации.

Введем обозначения: r(t) — стоимость продукции, произ­водимой за один год на единице оборудования возраста t лет;

u(t) — ежегодные затраты на обслуживание оборудования возраста t лет;

s(t) — остаточная стоимость оборудования возраста t лет;

Р — покупная цена оборудования.

Рассмотрим период N лет, в пределах которого требуется определить оптимальный цикл замены оборудования.

Обозначим через f_N (t) максимальный доход, получаемый от оборудования возраста t лет за оставшиеся N лет цикла использования оборудования при условии оптимальной стра­тегии.

Возраст оборудования отсчитывается в направлении тече­ния процесса. Так, t = О соответствует случаю использования нового оборудования. Временные же стадии процесса нумеру­ются в обратном направлении по отношению к ходу процесса. Так, N = 1 относится к одной временной стадии, остающей­ся до завершения процесса, а N = N — к началу процесса (рис. 29.1).

На каждом этапе N -стадийного процесса должно быть при­нято решение о сохранении или замене оборудования. Выбран­ный вариант должен обеспечивать получение максимальной прибыли.

Возраст оборудования

начало конец

0 1 2 3 t

……………….

N N-1 1 0

Стадии

Рис..1

Функциональные уравнения, основанные на принципе оптимальности, и имеют вид:

r(t)- u(t)+ f _{N -1} (t+1) - Сохранение

f _N (t)= max

s(t) – P + r(0) – f _N-1 (1)-Замена (1)

r(t)- u(t)- Сохранение

f ₁ (t)= max

s(t) – P + r(0) –u (0)- Замена (2)

Уравнение (1) описывает N-стадийный процесс, а (2) — одностадийный. Оба уравнения состоят из двух час­тей: верхняя строка определяет доход, получаемый при сохра­нении оборудования; нижняя — доход, получаемый при замене оборудования и продолжении процесса работы на новом обору­довании.

В уравнении (1) функция r(t) — u(t) есть разность между стоимостью произведенной продукции и эксплуатационными издержками на N-% стадии процесса.

Функция f _N-1 (t +1) характеризует суммарную прибыль от (N — 1) оставшихся стадий для оборудования, возраст которо­го в начале осуществления этих стадий составляет (t + 1) лет.

Нижняя строка (1) характеризуется следующим обра­зом: функция s(t)—P представляет чистые издержки по замене оборудования, возраст которого t лет.

Функция r(0) выражает доход, получаемый от нового обо­рудования возраста 0 лет. Предполагается, что переход от ра­боты на оборудовании возраста t лет к работе на новом обо­рудовании совершается мгновенно, т.е. период замены старо­го оборудования и переход на работу на новом оборудовании укладываются в одну и ту же стадию.

Последняя функция f _N-1 в (1) представляет собой доход от оставшихся N—1 стадий, до начала осуществления которых возраст оборудования составляет один год.

Аналогичная интерпретация может быть дана уравне­нию для одностадийного процесса. Здесь нет слагаемого вида fo(t + 1), так как N принимает значение 1,2,..., N. Равенство fo{t) = 0 следует из определения функции f _N(t).

Уравнения (1) и (2) являются рекуррентными соот­ношениями, которые позволяют определить величину f _N(t) в зависимости от f_N-1 (t+1). Структура этих уравнений показы­вает, что при переходе от одной стадии процесса к следующей возраст оборудования увеличивается с t до (t + 1) лет, а число оставшихся стадий уменьшается с N до (N — 1).

Расчет начинают с использования уравнения (1). Урав­нения (1) и (2) позволяют оценить варианты замены и сохранения оборудования, с тем чтобы принять тот из них, ко­торый предполагает больший доход. Эти соотношения дают возможность не только выбрать линию поведения при реше­нии вопроса о сохранении или замене оборудования, но и опре­делить прибыль, получаемую при принятии каждого из этих решений.

Пример 1. Определить оптимальный цикл замены оборудо­вания при следующих исходных данных: Р = 10, S(t) = 0, fit) = r(t) — u(t), представленных в табл. 29.1.

Таблица 1

N

F(t)

Решение. Уравнения (1) и (2) запишем в следующем виде:

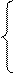f(t)+ f_N-1 (t+1)

f _N (t)= max

- p +f (0)+ f_N-1(1) (3)

f(t),

f ₁ (t)= max

- p +f (0)

Для N=1

f (0) 10

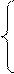
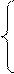
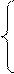
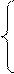
f ₁(0)= max = max 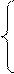= 10,

- p +f (0) -10+10

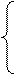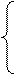f (1) 9

f ₁(1)= max = max = 9,

- p +f (0) -10+10

…………………………………………………………………………..

f (12) 0

f ₁(12)= max = max = 0.

- p +f (0) -10+10

Для N=2

f (0)+ f₁(1) 10+9

f ₂(0)= max = max =19,

- p +f (0)+ f₁(1) -10+10+9

f (1)+ f₁(2) 9+8

f ₂(1)= max = max =17,

- p +f (0)+ f₁(1) -10+10+9

…………………………………………………………………………………

Вычисления продолжаем до тех пор, пока не будет выпол­нено условие f₁(1)> f₂(2), т.е. в данный момент оборудование необходимо заменить, так как величина прибыли, получаемая в результате замены оборудования, больше, чем в случае ис­пользования старого. Результаты расчетов помещаем в табли­цу, момент замены отмечаем звездочкой, после чего дальней­шие вычисления по строчке прекращаем (табл. 2).

Таблица

FN(t)

N

N -1

f1(t)

1 0 0

f2(t)

9*

f3(t)

17^*

f4(t)

24^*

f5(t)

30^*

f6(t)

35^*

f7(t)

41^*

f8(t)

48^*

f9(t) f10(t)

54^* 60^*

f11(t)

65^*

f12(t)

72^*

Можно не решать каждый раз уравнение (29.3), а вычис­ления проводить в таблице. Например, вычислим f₄(t):

f₄(0) = f₁(0) + fз(1) = 10 + 24 = 34 > f₃(1) = 24,

f₄(1) = f₁(1) + fз(2) = 9 + 21 = 30 > f₃(1),

f₄(2) = f₁(2) + fз(3) = 8 + 18 = 26 > f₃(1),

f₄(3) = f₁(3) + f₃(4) = 7 + 17 = 24 > f₃(1),

f₄(4) = f₁(4) + f₃(5) = 6 + 17 = 23 < f₃(1).

Дальнейшие расчеты для f₄(t) прекращаем, так как

f₄(4) = 23 < f₃(1) = 24.

По результатам вычислений и по линии, разграничиваю­щей области решений сохранения и замены оборудования, на­ходим оптимальный цикл замены оборудования. Для данной задачи он составляет 4 года.

Ответ. Для получения максимальной прибыли от ис­пользования оборудования в двенадцатиэтапном процессе оп­тимальный цикл состоит в замене оборудования через каждые 4 года.

Дата добавления: 2014-11-08