Обозначения и сокращения

Решение.

Интенсивность потока обслуживания 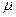=1/ 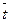_обс=1/3=0,333, интенсивность нагрузки 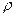=1,5.

1. Вероятность простоя контролеров-кассиров в течение рабочего дня:

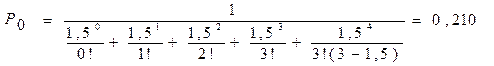
2. Вероятность застать всех контролеров-кассиров занятыми:

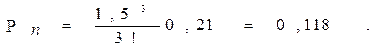
3. Вероятность очереди:

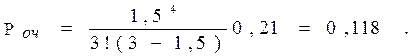
4. Среднее число заявок в очереди:

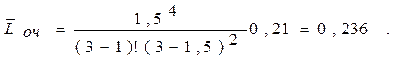
5. Среднее время ожидания заявки в очереди:

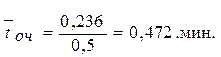
6. Среднее время пребывания заявки в СМО:

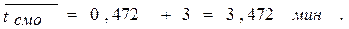
7. Среднее число свободных каналов:

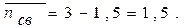
8. Коэффициент занятости каналов обслуживания:

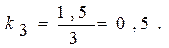
9. Среднее число посетителей в сберкассе:

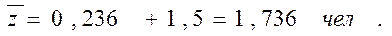
Ответ. Вероятность простоя контролеров-кассиров равна 21% рабочего времени, вероятность посетителю оказаться в очереди составляет 11,8%, среднее число посетителей в очереди 0,236 чел., среднее время ожидания посетителями обслуживания 0,472 мин.

m - число обслуживаемых агрегатов

n - число обслуживающих агрегатов

Р₀ - вероятность того, что в обслуживающем звене системы не имеется ни одно­го требования, т.е. все обслуживающие агрегаты свободны

М_ож - среднее число агрегатов, ожидающих обслуживания (средняя длина оче­реди)

К_пр - коэффициент простоя обслуживаемого агрегата

К_св - среднее число (математическое ожидание) свободных, т.е. простаивающих обслуживающих агрегатов

К_ис - коэффициент простоя обслуживающего агрегата

М_об - среднее число (математическое ожидание) требований, находящихся в об­служивающей системе, т.е. обслуживаемых и ожидающих в очереди

У_min - целевая функция (критерий оптимизации), включает в себя технико-экономические показатели обслуживаемых (С₁) и издержки (С₂), связанные с содержанием обслуживающего комплекса.

ЗАКЛЮЧЕНИЕ

Рассмотренные в данном курсе методы математического моделирования с/х процессов, естественно, не охватывают в полном объеме все многообразие этих методов. Тем не менее на основе рассмотренного материала можно составить представление о математическом моделировании как одном из инструментов (и порой весьма эффективном) будущей профессиональной деятельности. Важно знать об имеющихся возможностях и уметь их адаптировать к потребностям конкретной задачи. Одним из гарантов успеха также является возможность со­трудничества со специалистами по математическому моделированию, уметь ставить им задачу, владеть соответствующей терминологией, правильно делать вывод из полученных результатов.

Дата добавления: 2014-11-08