Основы теории массового обслуживания

ТМО (или система массового обслуживания СМО) представляет собой раздел прикладной математики, изучающей про­цессы, связанные с удовлетворением массового спроса на обслуживание како­го-либо вида услуг с учетом случайного характера спроса и обслуживания. Примерами таких процессов могут служить различного рода ремонтные пред­приятия, транспортные системы, поточные производства, в частности поточная организация уборки с/х культур.

§ 1. Основные понятия ТМО.

Потоком называют последовательность событий (наступающих, вообще го­воря, в случайные моменты времени).

Поток событий называется регулярным, если события следуют одно за дру­гим через строго определенные промежутки времени. Такой поток встречается сравнительно редко в реальных системах. Типичным для ТМО является случай­ный поток заявок. Для изучения свойств потоков введем ряд определений.

О₁. - Поток событий называют стационарным, если вероятность наступления того или иного числа событий за промежуток времени г зависит только от величины τ и не зависит от расположения промежутка времени τ на оси оt.

О₂. - Поток событий называется потоком без последствий, если для любых неперекрывающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.

О₃. - Поток событий называется ординарным, если вероятность попадания на элементарный отрезок времени ∆t двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.

Потоки событий, обладающие этими тремя свойствами, называют простейшими или пуассоновскими. Второе название связано с тем, что для него число
событий, попадающих на любой фиксированный интервал времени I, будет
распределено по закону Пуассона.

где (1)

Р_k(t) - вероятность наступления точно k событий за время t;

λ - плотность потока (среднее число событий, приходящееся на единицу времени).

Физический смысл величины λ - математическое ожидание числа требова­ний, поступивших в единицу времени, т.е. это характеристика того, сколь часто у обслуживаемого агрегата возникает технологическая (или иная) потребность в обслуживании.

Если известно число требований k, поступивших от одного агрегата за время
Т, то 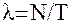1/час (2)

Тогда λt - это математическое ожидание числа требований, поступивших от этого агрегата за время t.

Т.о. если анализ потока требований приводит к заключению, что рассматри­ваемый поток является простейшим, то для его полной характеристики необхо­димо и достаточно вычислить величину λ. При этом заметим, что

это среднее время между поступлением двух заявок, поэтому

Х=1/1ср 1/ч (2')

(1ср - математическое ожидание промежутка времени между двумя заявками).

Отметим, что при сложении достаточно большого числа потоков, имеющих различные законы распределения, результирующий поток является простей­шим. На практике оказывается достаточно сложить 4-5 потоков, чтобы полу­чить поток, с которым можно оперировать как простейшим.

Важнейшей характеристикой функционирования обслуживающего звена сис­темы является продолжительность обслуживания одного требования. Это вели­чина выступает в качестве объективного критерия пропускной способности об­служивающего звена. В силу различных причин время обслуживания одинако­вых заявок носит случайный характер. Следовательно время обслуживания яв­ляется случайной величиной, распределенной по определенному закону. Обыч­но это показательный закон распределения, для которого функция распределе­ния имеет вид:

F(t) - вероятность того, что время обслуживания не превзойдет наперед задан­ной величины t;

ν - величина обратная среднему времени обслуживания, т.е.

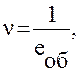
1/час, где (4)

t_об - математическое ожидание продолжительности обслуживания одной заявки физический смысл величины ν - математическое ожидание числа заявок, об­служенных в единицу времени.

Если N₁ - число обслуженных заявок, а Т₁ - общее время обслуживания этих заявок, то

t_об = T₁/N₁ (5)

И значит, - среднее время обслуживания одной заявки.

Остановимся теперь более подробно на анализе организации обслуживания при выполнении с/х производственных процессов.

1) Заявки на обслуживание посту­пают от ограниченного числа агрегатов, ограничено и число обслуживающих агрегатов. Это позволяет классифицировать системы обслуживания встре­чающиеся в с/х-й практике как системы с ограниченным числом обслуживающих звеньев.

2) Второе специфическое свойство организации систем обслуживания при вы­полнении с/х производственных процессов заключается в том, что любое требование на обслуживание не покидает систему до тех пор, пока не будет обслужено. Это позволит классифицировать подобную систему обслужива­ния как систему с ожиданием..

Перейдем теперь к общей формулировке задачи наиболее часто встречаю­щейся в с/х практике при организации поточного использования с/х техники.

Система обслуживания состоит из т обслуживаемых и п обслуживающих объектов.

Первые время от времени нуждаются в обслуживании, поэтому часть време­ни они находятся в системе обслуживания, а часть вне ее.

Поток поступающих от них требований на обслуживание ограничен, т.е. в системе обслуживания не может находится одновременно более т заявок.

Поток требований обладает свойствами простейшего потока. Частота поступ­ления в обслуживающее звено системы от одного агрегата, т.е. частота возвра­щения требования в обслуживающую систему равна λ (1/час).

Каждый агрегат, прибывший на обслуживание, покидает систему вне зави­симости от длины очереди только тогда, когда он будет обслужен, т.е. система относится к числу систем с ожиданием.

Каждый из обслуживающих агрегатов системы может одновременно обслу­живать только одно требование.

Если в момент поступления очередного требования имеются свободные агре­гаты звена обслуживания, то один из них немедленно приступает к обслужива­нию этого требования. Если же все эти агрегаты заняты, то требование ждет, по­ка освободится один из них.

Если число агрегатов, нуждающихся в обслуживании, превышает количество обслуживающих агрегатов, то образуется очередь.

Требуется оценить качество функционирования этой системы, т.е. количест­венно охарактеризовать эффективность использования общих групп машин, со­вместно работающих в потоке.

Существует целый ряд критериев, позволяющих оценить качество функцио­нирования рассматриваемой системы.

1. Прежде всего, таким критерием является отношение средней длины очереди к числу агрегатов, составляющие обслуживаемое звено системы. Это отноше­ние называется коэффициентом простоя обслуживаемого объекта.

2. В качестве другого критерия используют отношение среднего числа простаи­вающих обслуживающих агрегатов к их общему числу. Это отношение назы­вается коэффициентом простоя обслуживающего агрегата. Представляют интерес также и такие критерии как:

- средняя длина очереди;

- вероятность иметь в очереди больше (меньше), чем заданное число требова­ний;

- среднее число простаивающих обслуживающих агрегатов; и т.п.

Коэффициенты простоя обслуживаемого и обслуживающего агрегатов наи­более полно характеризуют коэффициент использования машин, т.к. дают воз­можность оценить величину потерь времени каждой из групп машин при со­вместной их работе в потоке.

Т.к. обслуживаемое звено системы состоит из n агрегатов, то в любой мо­мент времени эта система может находиться в одном из (m + 1) состоянии:

1) Свободны все каналы обслуживания, очереди нет (к = 0)

2) Занят только один канал обслуживания, очереди нет (к = 1)

3) Заняты 2 канала обслуживания, очереди нет (к = 2)

………………………….

n+1) Заняты все n каналов обслуживания, очереди нет (к = n)

n+2) Заняты все каналы, одна заявка в очереди (к = n + 1)

………………………….

m) Все каналы заняты, (m - n - 1) - заявок в очереди (к = m - 1)

m + 1) Все каналы заняты, (m - n) - заявок в очереди (к = m)

Отметим, что очередь из обслуживаемых агрегатов возникает только тогда, когда число обслуживающих агрегатов n будет меньше числа обслуживаемых, т.е. m > n.

Изложим методику определения так называемых оценочных критериев, не приво­дя вывода применяемых формул.

Для определения величины коэффициента простоя обслуживаемого агрегата необходимо найти среднее число агрегатов M_ож, ожидающих обслуживания (среднюю длину очереди). Это значение вычисляется по формуле

k - число требований, находящихся в обслуживаемом звене системы,

m - число обслуживаемых агрегатов,

n - число обслуживающих агрегатов,

P_k - вероятность того, что в обслуживающем звене находится точно к требований.

Для определения Р_k используют формулы:

(7)

Здесь Р₀ - вероятность того, что в обслуживающем звене системы не имеется ни одного требования, т.е. все обслуживающие агрегаты свободны.

ν - величина обратная среднему времени обслуживания.

Р₀ вычисляется по формуле:

Формула (7) используется для определения вероятности пребывания в об­служивающем звене системы точно к требований, когда число этих требований не превосходит числа обслуживающих агрегатов, т.е. к ≤ n.

Формула же (8) применима для тех состояний системы, когда имеется оче­редь на обслуживание. Ясно, что сумма всех вероятностей равна 1.

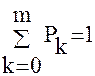
Итак, М_ож - это среднее число обслуживаемых агрегатов, простаивающих в

очереди в ожидании обслуживания и не участвующих из-за этого в выполнении производственного процесса.

Время ожидания в очереди является потерянным для производства. Тогда, как время, расходуемое непосредственно на обслуживание агрегата является не­обходимым для нормального хода выполнения рассматриваемого производст­венного процесса.

Зная величину М_ож, можно определить значение коэффициента простоя об­служиваемого объекта.

К_пр-М_ож/m (11)
Или, используя (6)

физический смысл этого коэффициента состоит в том, что он показывает, ка­кую долю времени смены каждый обслуживаемый агрегат в среднем проводит в ожидании обслуживания. Следовательно, этот коэффициент характеризует непроизводительные затраты времени, обусловленные структурой всей систе­мы, т.е. соотношением m и n.

В практике экономических расчетов в ряде случаев необходимо определить ма­тематическое ожидание М_об числа требований, находящихся в обслуживающей системе, т.е. обслуживаемых и ожидающих в очереди.

Или в развернутом виде:

(14)

Величина М_об показывает, сколько агрегатов практически не участвуют в вы­полнении производственного процесса при данной структуре системы из-за не­обходимости контакта с ее обслуживающем звеном.

При необходимости вычислить вероятность того, что длина очереди М не превзойдет заданного числа N₁, используют формулу:

(15)

Вероятность же того, что число требований, ожидающих начала обслужива­ния (длина очереди), больше некоторого числа N₁ состоит:

(16)

Заметим, что М - это текущее значение числа агрегатов, ожидающих очередь на обслуживание. Потребность в таком расчете может возникнуть, например, при планировании размеров подъездных площадок у пунктов разгрузки (погрузки) грузов, заправочных станций и т.д. Если при этом возникает необхо­димость вычислить вероятность того, что число агрегатов М', находящихся в зоне обслуживания (т.е. обслуживающихся и ожидающих обслужива­ния), не превзойдет заданного числа N₂, то расчет выполняют по формуле:

(17)

Рассмотренные нами критерии достаточно полно характеризуют количест­венно функционирование только обслуживаемого звена системы. Для оценки качества функционирования всей системы в целом необходимо определить со­ответствующие критерии для ее обслуживающего звена.

Для того, чтобы найти коэффициент простоя К_пс обслуживающего агрегата, нужно определить среднее число N_св (математическое ожидание) свободных, т.е. простаивающих обслуживающих агрегатов:

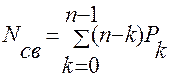(18)

Подставив в это выражение значение Р_к в соответствии с формулой (7), получаем:

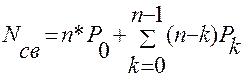(19)

(объяснить пределы суммирования)

Напомним, что величина Nсв показывает сколько обслуживающих агрегатов в среднем за смену не участвуют в работе системы, т.е. остаются свободными. Зная величину N_св, вычисляем значение коэффициента простоя обслуживаю­щего агрегата К_пс.

(20)

Этот коэффициент показывает какую долю времени смены каждый из обслу­живающих агрегатов простаивает.

Приведенный выше пример оценочных критериев позволяет достаточно пол­но охарактеризовать функционирование всей системы обслуживания, включая как агрегаты, от которых исходят требования, так и агрегаты обслуживающего звена.

Рассчитав критерии для обслуживаемых и обслуживающих агрегатов, необ­ходимо найти оптимальный состав системы. Для этого для каждого варианта проводятся расчеты потерь от простоев обслуживаемого и обслуживающего звеньев. Оценка различных вариантов проводится по минимуму указанных вы­ше потерь от простоев. Критерий оптимизации (целевая функция) включает в себя технико-экономические показатели обслуживаемых агрегатов (С₁) и из­держки (С₂), связанные с содержанием обслуживающего комплекса, т.е.

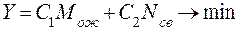(21), где

С₁, С₂ - потери, соответственно от простоев обслуживаемых и обслуживающих агрегатов, руб./ч

Методика составления коэффициентов С₁ и С₂ определяется содержанием конкретной задачи.

С₁=С_в+С_к+С_н, руб./ч, где

С_в - затраты на восстановление

С_н - затраты (потери) от недобора продукции из-за простоя машин

С_к - затраты на устранение различного рода неисправностей.

С₂=q₁+q₂+q₃, где

q₁ - затраты на содержание (амортизацию) ремонтно-технических и транспорт­ных средств

q₂ - оплата труда обслуживающего персонала

q₃ - затраты на топливо смазочные материалы и вспомогательное оборудование.

В каждом конкретном случае возможен учет и др. показателей для целевой функции.

Естественно, целевая функция (21) не исчерпывают всех возможных подходов к составлению критериев оптимизации.

Задача 1.

Требуется рассчитать оптимальное количество заправочных колонок внутрихозяйственной АЗС для автомобилей КАМАЗ и найти показатели про­цесса обслуживания. При этом расчеты производить для следующих количеств автомобилей: 4, 9, 14, 19, 24, полагая, что средняя длительность промежутка времени между двумя заправками одного автомобиля составляет 5,33 часа (1,5 раза за 8 часовую смену), а средняя продолжительность одной заправки 15 ми­нут. Потери соответственно от простоев автомобиля и колонки составляют 793 руб./час и 131,5 руб./час. Установить корреляционную зависимость опти­мального числа колонок от числа автомобилей и корреляционную зависимость минимума потерь из-за простоев обслуживаемого и обслуживающего звеньев от числа автомобилей.

РЕШЕНИЕ.

1) Подготовка данных для ЭВМ: m = 4, 9, 14, 19,24

2) Подготовленные данные для каждого значения m вводятся в ЭВМ (программа and.exe). В итоге получаем 5 групп результатов, которые объединяем в одну таблицу.

- плотность потока (среднее число событий, приходящиеся на единицу вре­мени)

- величина обратная среднему времени обслуживания

m	n	Р0	Мож	Кпр	Nсв	Кис	Моб	Уmin
		0,822	0,026	0,007	0,822	0,822	0,205	128,79
		0,659	0,012	0,001	0,938	0,469	0,415	132,44
		0,517	0,052	0,004	0,857	0,428	0,678	153,72
		0,416	0,018	0,001	1,316	0,439	0,870	187,02
		0,328	0,047	0,002	1,268	0,423	1,122	203,88

Зависимость n от m и У_min от m будем искать в виде уравнений линейной регрессии, т.к. с возрастанием m возрастают значения величин n и У_min.

3) n = km + b

Вычислим сначала коэффициент корреляции

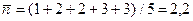
m_r= (1-0,9449112) / 5 = 0,04791575

r = 0,9449112 > 3×0,05 = 0,15 ≈ 3 m_r

Зависимость тесная

к = (4 -1+9 -2+14 -2+19 -3+24 -3-5 -14 -2,2)/[(4-14)²+(9-14)²+(14-14)²+(19-14)² +(24-14)² =0,1

в = 2,2-0,1×14 = 0,8

n = 0,1m+0,8

n(m₁)=0.1*4+0.8-1.2; ∆n₁=0.2

n₂=1.7 ∆n₂=0.3

n₃=2.2 ∆n₃=0.2

n₄=2.7 ∆n₄=0.3

n₅=3.2 ∆n₅=0.2

Средняя абсолютная ошибка

∆_ср = (0,2+0,3+0,2+0,3+0,2) / 5 = 0,24

Средняя относительная ошибка и максимальная относительные ошибки:

4) У_min = km+b

m=14

У_min = (128,79+132,44+153,72+187,02+203,88) / 5 = 161,17

r = 0.97337522>3*0.024 = 0,072 = 3m_r

Зависимость тесная

k = (128,79*4+132,44 -9+153,72 -14+187,02 -19+203,88 -24-5 -14-161,17):

:[(4-14)²+(9-14)²+(14-14)²+(19-14)²+(24-14)²] = 4,095203

b = 161,17- 4,095203m = 103,8816 n = 4,1m+103.9

Средняя абсолютная ошибка

∆ = (8,52758+8,288431+7,494446+5,329544+1,713531) / 5 = 6,270707

Средняя относительная погрешность

Максимальная относительная погрешность

На практике часто возникает задача прогнозирования поведения систем массового обслуживания. Изложенная выше методика расчета позволяет решать эту задачу. Действительно, значения оценочных критериев могут быть вычислены при различных соотношениях между числом обслуживаемых и об­служивающих агрегатов (что было сделано в примере). Это позволяет устано­вить корреляционную зависимость (достаточно тесную) между различными па­раметрами изучаемой системы и на их основе прогнозировать поведение систе­мы. Например, в условиях рассмотренного примера, если m=10, то n=0,1*10+0,8≈2, У_min = 4,095-10+103,88=40,95+103,88=144,83 руб./ч или m=30, n=0,1*30+0,8=3,8≈4, У_min = 4,095 -30+103,88=226,73 руб./ч.

Располагая данными о коэффициентах простоя (К_пр, К_пс) обслуживаемых и обслуживающих агрегатов можно выразить производительностью W_i и W_j того и другого звена системы следующим образом:

(23)

; (24)

где W_i и W_j - производительность обслуживаемого и обслуживающего агре­гата при его автономной работе, т.е. без учета возможных простоев, обуслов­ленных организаций выполнения поточного производства при данной структуре системы обслуживания.

Уравнения (23) и (24) позволяют анализировать как изменяется производи­тельность любого звена системы при изменении числа агрегатов, входящих в это звено.

Следует отметить, что методы ТМО с успехом применяются не только при решении задач, связанных с оценкой и проектированием организаций смежных процессов поточного с/х производства, а также с анализом эффективности ис­пользования с/х техники при этом.

С помощью этих методов можно вести проектные расчеты по организации службы технического обслуживания и ремонта с/х техники, а также по организации службы управления с/х производством. Однако, для решения этих задач в ряде случаев требуется иной формульный аппарат, отра­жающий их специфику. Напомним, что мы рассматриваем принципы расчета систем обслуживания только для ограниченного потока требований. Подобные системы являются далеко не единственными в экономической практике. На­пример, могут быть рассмотрены системы с ограничениями ожидания в очере­ди (по времени или по длине очереди) или системы с отказами, когда все кана­лы обслуживания заняты, немедленно получает отказ, покидает систему и в дальнейшем процессе обслуживания не участвует.

Задача 2. Сберкасса имеет трех контролеров-кассиров (n=3) для обслуживания вкладчиков. Поток вкладчиков поступает в сберкассу с интенсивностью λ=30 чел./ч. Средняя продолжительность обслуживания контроллером-кассиром одного вкладчика 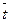_обс =3 мин.

Определить характеристики сберкассы как объекта СМО.

Дата добавления: 2014-11-08