Тема 7.4. Интеграл Фурье. Преобразование Фурье

Вопросы для самопроверки

1. Сформулируйте условия Дирихле и теорему Дирихле.

2. В чем состоит особенность разложения в ряд Фурье четных и нечетных функций?

3. Выведите формулу для коэффициентов Фурье.

4. Приведите пример ортогональной системы функций на промежутке (-к,к).

5. Запишите ряд Фурье в комплексной форме.

6 Запишите равенство Парсеваля для функций, заданных на промежутке

(-7EJC).

Учебники: [16, гл. 17, §§ 5.32 - 5.34], [19, гл. 1, §§ 9 - 11], [28, гл. 2].

Аудиторная работа: [7, гл. 4, § 9.4, №№ 272, 276, 280, 282 (а)], [20, ч. 2, гл. 12, §§ 7.3 - 7.4, №№ 12. 513, 12.520], [31, №№ 191, 198, 213, 216, 221, 232, 244].

Самостоятельная работа: [7, гл. 4, § 9.4, №№ 273 - 275, 277, 282 (б)], [20, ч. 2, гл. 12, §§ 7.3 - 7.4, №№ 12. 514, 12.515], [31, №№ 195, 196, 214, 218, 224, 225, 228, 235, 242].

Функция f(x), абсолютно интегрируемая на всей вещественной оси 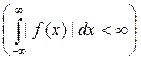и кусочно-непрерывная на каждом конечном отрезке этой оси, может быть представлена в виде интеграла Фурье

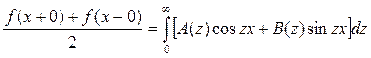, (7.4.1)

где

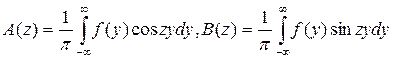. (7.4.2)

В случае четной функции (f(-х) = f(х))

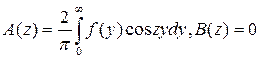, (7.4.3)

а в случае нечетной функции (f(-х) = -f(x))

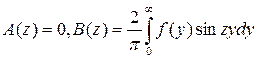, (7.4.4)

Пример 7.4.1. Представить функцию 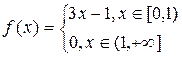интегралом Фурье, продолжив ее на отрицательную полуось четным образом.

Решение. График функции изображен на рис. 7.4.1.

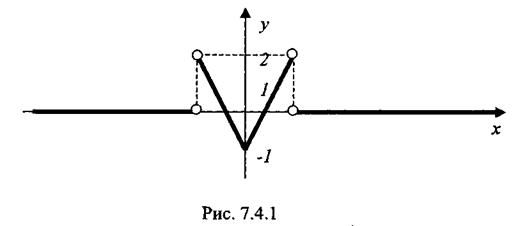Продолжение на отрицательную полуось функции f(x) проведено чет­ным образом, поэтому, воспользуясь формулой (7.4.3) (B(z) = 0), получим

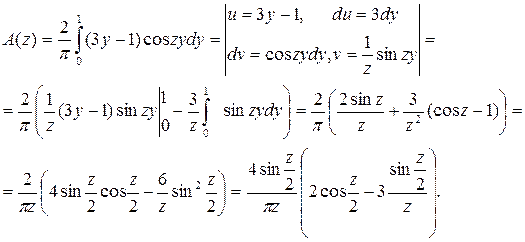
Таким образом, .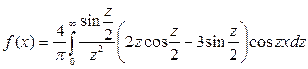

Если задана функция f(x), то функцию

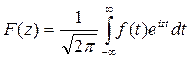(7.4.5)

называют преобразованием Фурье функции f(x), а обратное преобразование Фурье имеет вид

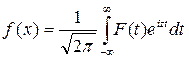(7.4.6)

Для четных функций имеет место косинус-преобразование Фурье

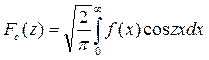(7.4.7)

и обратное косинус-преобразование Фурье

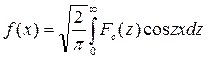. (7.4.8)

Для нечетных функций записывается синус-преобразование Фурье

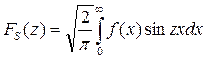(7.4.9)

и обратное синус-преобразование Фурье

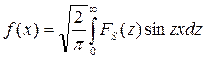. (7.4.10)

Пример 7.4.2. Найти преобразование Фурье функции

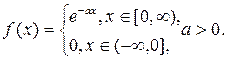
Решение. По формуле (7.4.5) находим

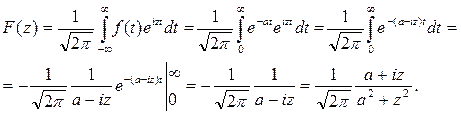
Пример 7.4.3. Решить интегральное уравнение

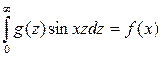, где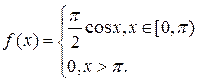

Решением интегрального уравнения будет синус-преобразование Фу­рье (7.4.9) функции 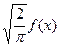, а именно:

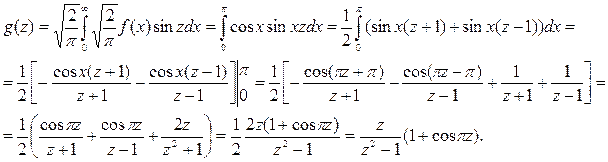
Замечание. В ряде учебников [16, 19] преобразование Фурье (7.4.5) записывают в виде 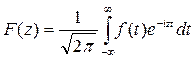, тогда обратное преобразование Фурье (7.4.6) имеет вид .

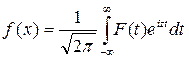Дата добавления: 2014-11-20