Контрольной работы №4

Дополнение 7.1. Образец выполнения и оформления

Вопросы для самопроверки

1. Приведите различные формы записи преобразования Фурье.

2. В чем состоит различие между представлениями функций в виде ряда и в виде интеграла Фурье?

3. Сформулируйте основные свойства преобразования Фурье.

После изучения тем раздела 7 студент должен выполнить задания № 3 контрольной работы № 4.

«Кратные интегралы. Ряды Фурье»

1. Построить область интегрирования и изменить порядок интегрирования:

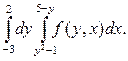
Решение. Изобразим на чертеже (рис. Д.7.1) линии x = y² -1 и x = 5 - y (или y² = x + 1, x + y = 5). Первая – представляет собой параболу с вершиной (-1,0), ветви направлены вправо вдоль оси ОХ. Решая систему

находим координаты точек пересечения: А(3,2), (8,-3).

Для изменения порядка интегрирования область D следует «разрезать» на две части D₁ и D₂ (D₁ соответствует x є [-1,3]), поскольку в D₁ и D₂ при фиксированном x = const линия входа будет одна и та же 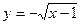, а линии выхода – разные: 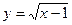при x<3 и y = 5 - x при x>3. Имеем

2. Найти объем тела, ограниченного поверхностями: z = x² + y² и z = 4x. Тело (G) ограничено параболоидом вращения и наклонной плоскостью, проходящей через его вершину,

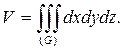
Решение. Исключая z из системы 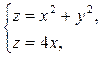получим x²+y²=4x.

На плоскости XOY это уравнение задает окружность, центр которой смещен на две единицы вправо по оси ОХ. Ограниченный этой окружностью круг представляет собой проекцию (G) на XOY. Вычисление удобнее проводить в цилиндрических координатах

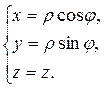
Уравнение линии x²+y²=4x преобразуем к виду ρ² = 4ρcosφ, или ρ = 4cosφ. Из условия ρ ≥ 0 видно, что φ ≥ 0, т.е. 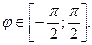. Для того, чтобы лучше представить себе пределы интегрирования по z, целесообразно сделать рисунок.

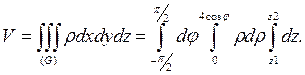
Здесь пределы по φ взяты из 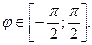, по ρ - от входа ρ=0 до ρ из уравнения окружности,

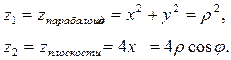
Имеем:

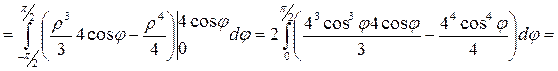
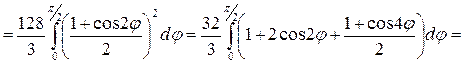
Ответ: V = 8π (ед³).

3. Найти площадь части сферы x² + y² + z² = 9, вырезанной цилиндром x² + y² = 3y.

Решение. Прежде всего, обратим внимание на то, что поверхность состоит из двух частей, симметричных относительно плоскости z = 0. Достаточно найти площадь части , а ответ умножить на 2.

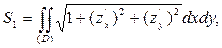
где D - проекция части сферы на плоскость XOY. В нашем случае D представляет собой круг, ограниченный линией x² + y² = 3y. Поскольку из уравнения верхней части сферы имеем

площадь будет равна

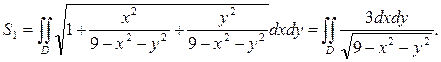
Этот интеграл проще вычисляется в полярных координатах. Запишем уравнение кривой x² + y² = 3y: x = ρcosφ, y = ρsinφ, ρ² = 3ρsinφ, или ρ = 3sinφ.

Заметим, что ρ ≥ 0, поэтому sinφ ≥ 0, φє[0;π].

Для упрощения вычислений обратим внимание на симметрию линии ρ = 3sinφ относительно вертикальной оси.

Осталось домножить ответ на 2.

S = 2S₁ = 18(π-2) (ед²).

Ответ: 18(π-2)ед².

4. Найти производную скалярного поля 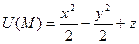в точке М₀(2;1;1) по направлению прямой в сторону возрастания поля.

Решение. Найдем 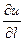по формуле , где градиент скалярного поля

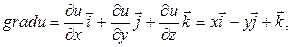
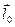- единичный вектор направления (1;0;2), т.е. .

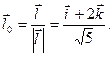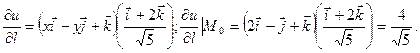
Ответ: .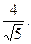

5. Найти векторную линию поля 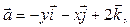, которая проходит через точку (3;0;0).

Векторная линия поля 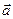– это линия, в каждой точке которой касательная имеет направление поля 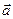. Векторные линии определяются из системы дифференциальных уравнений.

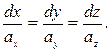
В нашем случае 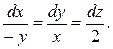Разделив переменные, имеем:

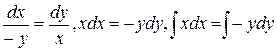
x² = -y² + c₁², x² + y² = c₁².

Для того, чтобы решить уравнение 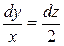, удобнее уравнение x² + y² = c₁² преобразовать к виду x = c₁cost, y =c₁sint.

Тогда

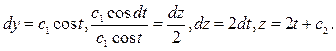
Уравнение векторных линий .

Точка (3;0;0) соответствует значению t = 0, тогда c₁ = 3, c₂ =0.

Ответ. x = 3cost, y =3sint, z = 2t.

6. Найти поток векторного поля 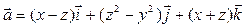через часть боковой поверхности конуса z² = x² + y², ограниченную плоскостями.

Решение. Первый способ. Поток можно найти непосредственно из определения в виде интеграла по площади поверхности: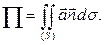

1) Находим единичный вектор нормали 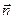к поверхности z² = x² + y² или x² + y² - z² = 0(f(x,y,z) = 0).

2) Находим .

3) Выразим z из уравнения конуса (для z≥0) , находим dσ:

4) Обозначим через D проекцию S на OXY. Поскольку z=1 ограничивает поверхность z² = x² + y², то D будет ограничена окружностью x² + y² = 1.

Здесь следует выразить z из уравнения поверхности .

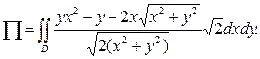
Переходим к полярным координатам:

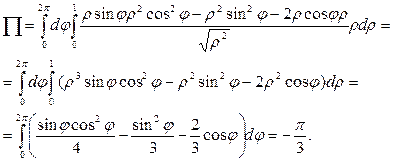
Второй способ. Воспользуемся теоремой Остроградского-Гаусса

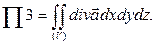
Искомый поток 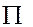найдем как разность потоков через замкнутую поверхность и 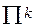потока через «крышку», т.е. через часть плоскости z=1.

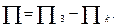
Находим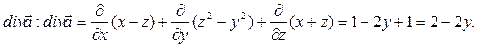

1) . Удобно перейти к цилиндрическим координатам x = ρcosφ, y = ρsinφ, z = z. Пределы интегрирования φє[0;2π], ρє[0;1] (см. проекцию конуса на XOY), , т.е. zє[ρ;1].

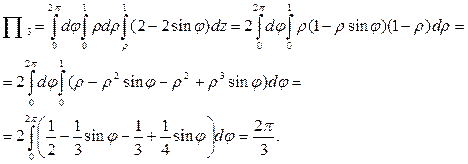
2) Найдем поток через «крышку» z=1, у которой вектором нормали является 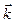, а dσ = dxdy. Найдем

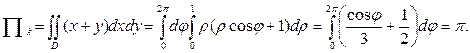
3) Находим .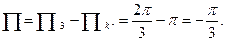

Как видно, ответы совпадают при двух способах вычисления.

Ответ: -π/3.

7. Убедимся в том, что поле потенциально и найти его потенциал.

Решение. Находим

при всех x, y, z. Следовательно, поле 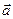- безвихревое.

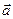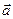Задача нахождения потенциала u поля (т.е. ) равносильна задаче восстановления функции u(x, y, z) по ее полному дифференциалу . В силу того, что - безвихревое, интеграл не зависит от пути интегрирования, поэтому в качестве пути удобно взять ломаную

где L₁ - отрезок, соединяющий (0;0;0) и (х;0;0) (здесь dy=0, dz=0, y=0, z=0),

L₂ - соединяет (х;0;0) и (х;у;0) (здесь dx=0, dz=0, z=0) и, наконец, L₃ соединяет (х;0;0) и (х;у;z) (здесь dx=0, dy=0). Имеем:

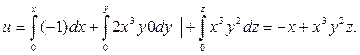
Потенциал поля определен с точностью до константы:

u(x,y,z)=-x+x³y²z+C.

8. Исследовать на сходимость числовые ряды:

а) б)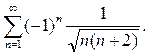

Дата добавления: 2014-11-20