Вопросы для самопроверки. 1. Объясните различие между необходимым и достаточным признаками сходимости ряда

1. Объясните различие между необходимым и достаточным признаками сходимости ряда.

2. Сформулируйте и докажите достаточные признаки сходимости числовых рядов.

3. Как произвести оценку остатка ряда:

а) с положительными членами;

б) с чередующимися по знаку членами?

4. Приведите пример условно сходящегося ряда.

5. Докажите признак Лейбница.

Тема 7.2. Функциональные ряды. Приложения рядов к приближенным вычислениям. Приближенное решение дифференциальных уравнений.

Учебники: [16, гл. 17, §§ 2.7 - 2.9, 3.10 - 3.13].

Аудиторная работа: [3, №№ 2802, 2805, 2810, 2817, 2820, 2825, 2855, 2860, 2863, 2878, 2882, 2886, 2898, 2827, 2829, 2903, 2931, 2937], [7, кн. 2, гл. 4, §§ 5 - 7, №№ 106, 11, 115, 118, 122, 123, 128, 130, 138, 141, 142, 151, 155, 158, 171, 175, 192, 195, 205, 208, 211, 214], [20, ч. 2, гл. 12, §§2-4, №№ 12.145, 12.146, 12.169, 12.172, 12.190, 12.214, 12.264, 12.295, 12.297, 12.327, 12.329], [34, гл. 3.2, №№ 1.2, 1.15, 2.1, 2.14, 3.14, 3.16, 4.2, 4.14, 5.11, 5.14, 6.10, 8.1, 8.12, 9.1, 11.12, 12.3, 12.11, 13.2,13.12].

Самостоятельная работа: [3, №№ 2803, 2806, 2812, 2814, 2818, 2819, 2828, 2834, 2856, 2857, 2859, 2864, 2879, 2880, 2883, 2889, 2900, 2901, 2921, 2933, 2935], [7, кн. 2, гл. 4, §§5-7, №№ Ю8, 111, 114, 116, 121, 124, 129, 131, 133, 137, 140, 141, 147, 150, 154, 159, 172, 175, 194, 196, 201, 206, 207, 210, 212, 216], [20, ч. 2, гл. 12, § 2 - 4, №№ 12.147, 12.149 (z заменить на S), 12.168, 12.174, 12.176, 12.183, 12.191, 12.198, 12.215, 12.225, 12.233, 12.265, 12.266, 12.296, 12.300, 12.326, 12.328], [34, гл. 2, 3.2, № №1.1, 1.3, 1.7, 1.20, 2.2, 2.7, 2.11, 2.23, 3.1, 3.6, 3.21, 4.1, 4.4, 4.8, 4.15, 4.21, 5.20, 5.22, 5.24, 6.4, 6.22, 8.2, 8.4, 8.18, 9.2, 9.6, 11.9, 11.18, 12.4, 12.11, 13.4, 13.20, 13.21].

Функциональным рядом 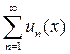называется ряд, каждый член которого u_n(х) есть функция от х. При фиксированном значении х = х₀ функцио­нальный ряд становится числовым рядом. Множество всех значений х, при которых функциональный ряд сходится, называется областью сходимости. Область сходимости функционального ряда, как правило, находят по извест­ным признакам сходимости (Даламбера, радикальный Коши), считая значе­ние х фиксированным.

Пример 7.2.1. Найти область сходимости функционального ряда

.

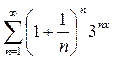Решение. Выпишем общий член ряда 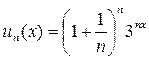и применим радикальный признак Коши

.

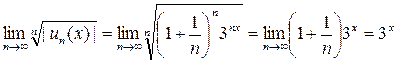Ряд сходится, если 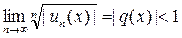, т.е. 3^х<1. Из последнего неравенства вытекает условие х < 0. Таким образом, исходный ряд сходится при х<0, расходится (|q(x)|>1) при х>0. При х=0 необходимо провести дополнительное исследование на сходимость соответствующего числового ряда, т. к. радикальный признак Копій не дает ответа на вопрос, сходится ряд или расходится .

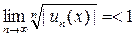Подставим в исходный ряд 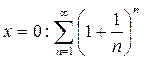- расходящийся ряд, т. к. 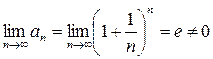(не выполняется необходимый признак сходимости). Итак, ряд сходится при х < 0.

Решение. Разложение функции sinх в ряд в окрестности 0 имеет вид .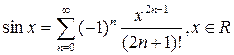

Исходя из этого разложения, находим

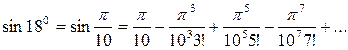
Полученный знакочередующийся ряд является рядом, рассматривае­мым в признаке Лейбница (7.1.2), а остаток этого ряда не превосходит по абсолютной величине первого отброшенного члена 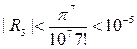. Поэтому .

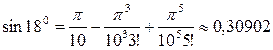Пример 7.2.4. Вычислить 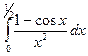с точностью до 10^-3.

Решение. Воспользуемся разложением .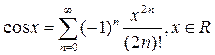

.

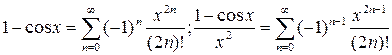Подставляя полученное выражение в интеграл, вычисляем

.

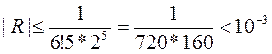Таким образом,

.

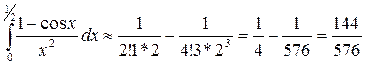Пример 7.2.5. Найти сумму ряда .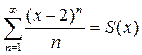

Решение. Прежде всего выясним, при каких значениях х ряд, сходится к функции S(x). По формуле (7.2.1) находим .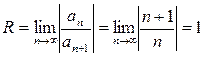

Таким образом, |х-2|<1, -1<х-2<1, 1<х<3. Проведем исследова­ние на сходимость на границе области сходимости (|х-2| = 1, х₁ = -1, х₂ = 3).

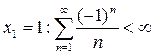(ряд типа (7.1.2) сходится);

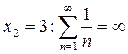(гармонический ряд расходится).

Областью сходимости исходного ряда является множество значений хє[1,3).

Продифференцируем исходный ряд, используя теорему о почленном дифференцировании равномерно сходящихся рядов

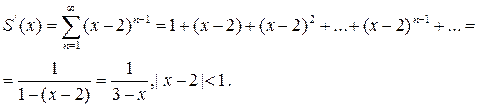
Откуда находим .

Константу интегрирования С определим из условия S(2) = 0, а именно: 0=-lnl+С, откуда получаем С = 0.

Таким образом, .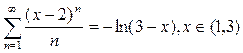

Пример 7.2.6. Найти три первых отличных от нуля члена разложения в степенной ряд решения y = у(х) дифференциального уравнения у' = sinx + у², удовлетворяющего начальному условию у(0) = 1 (задача Коши).

Решение. Будем искать решение в виде

Используя условие у(0)=1, почленным дифференцированием исход­ного уравнения, находим

.

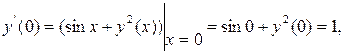
Таким образом, .

Дата добавления: 2014-11-20