Интегральные теоремы

Циркуляция и поток векторного поля

Литература: [3, №№ 4405 - 4408, 4450 - 4453, 4458 - 4465; 5, §§ 3.12 -3.15; 6, гл 6, §§3-4; 20, гл. 2, §§7-11].

Пусть а - непрерывное векторное поле в области Ω, Г - кусочно-гладкая ориентированная кривая в Ω. Линейным интегралом от а по Г (работой сило­вого поля) называется интеграл

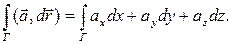(6.5.14)

Если Г - замкнутая кривая, то этот интеграл называется циркуляцией поля а по Г.

Пусть S - кусочно-гладкая ориентированная поверхность Ω, n - еди­ничный вектор нормали к поверхности, задающий ее ориентацию, n = (cosα; cosβ; cosγ). Потоком векторного поля а через поверхность S в направлении вектора нормали к поверхности n называется интеграл

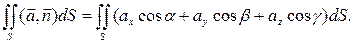(6.5.15)

Литература: [3, №№ 4457 - 4465; 5, §§ 3.12 - 3.15; 6, гл 6, §§ 3 - 4; 20, гл.2,§§8-11].

Пусть u - непрерывное дифференцируемое скалярное поле в Ω, Г- ку­сочно-гладкая ориентированная кривая в Ω, с началом А и концом В. Тогда

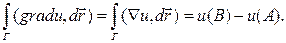(6.5.16)

Если кривая Г лежит на поверхности уровня поля u, то работа поля grad u вдоль Г равна нулю.

Пусть а - непрерывно дифференцируемое векторное поле в области Ω, S - кусочно-гладкая ориентированная единичным вектором нормали n по­верхность в Ω с краем dS, ориентированным согласованно с ориентацией по­верхности. Тогда имеет место теорема Стокса

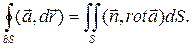(6.5.17)

Таким образом, циркуляция поля а по краю поверхности S равна пото­ку ротора поля а через эту поверхность.

Пусть G - ограниченная область с кусочно-гладкой границей dG, ори­ентированной единичным вектором внешней нормали n. Тогда имеет место теорема Остроградского - Гаусса

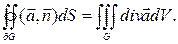(6.5.18)

Пример 6.5.1. Найти поток поля а = іу + jz + кх через поверхность 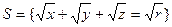, нормаль к которой направлена от начала координат.

Решение. Очевидно, div а = 0. Воспользуемся теоремой Остроградско­го - Гаусса.

Рассмотрим область G - криволинейный тетраэдр ОАВС (рис.6.5.1). Часть его границы, лежащей в плоскости Оху, обозначим S₁, в плоскости Oyz -S₂ и в плоскости Oxz - S₃. Потоки поля через S, S₁, S₂, S₃ (нормаль внешняя к G) обозначим соответственно П, П₁, П₂, П₃.

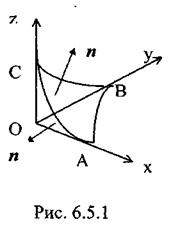По теореме Остроградского - Гаусса 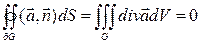, то есть П + П₁ + П₂ + П₃ = 0, а П = -(П₁ + П₂ + П₃).

Вычислим, например, П₃. Здесь n =(0; -1; 0), a =j z + к х. За параметры на S₃ - криволинейном треугольнике АОС - возьмем х и z. Дуга АС задается уравнением 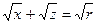, то есть 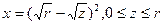. Находим

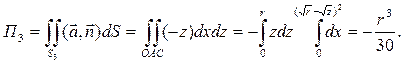
Таковыми же являются П₁ и П₂. Следовательно, П = 3 r³/30 = r³/10.

Пример 6.5.2. Пусть γ - часть линии пересечения эллипсоида 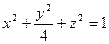с цилиндром х² + у² =1, лежащая в замкнутой области х ≥ 0, у ≥ 0 и ориентированная по возрастанию ординат точек. Найти работу поля а = уi + + хj + zk:

1) вдоль γ;

2) вдоль γ і - части γ, лежащей в первом октанте.

Решение. Легко найти, что 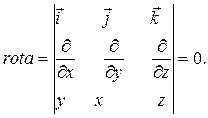Воспользуемся формулой Стокса (6.5.17). Замкнем γ дугой γ * = АС, являющейся пересечени­ем эллипсоида с плоскостью OYZ. Контур Г= АВСА - это граница части по­верхности эллипсоида, вырезанной цилиндром. По формуле Стокса

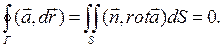
Отсюда

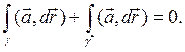
Дугу γ* замкнем отрезком АС, направленным от А к С. Получившийся контур служит границей части плоскости Oyz. Ввиду того, что rot a = 0, как и выше, получим

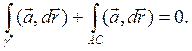
На отрезке АС а =уi + (√3/2)к, dr = {0; dy; 0}, поэтому

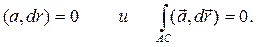
Отсюда следует, что и

1-й способ. Вычислим работу по γ* непосредственно, используя параметризацию γ *. Полагая х = cosφ, у = sinφ, 0 ≤ φ ≤ π/2, из уравнения эллипсоида имеем z = (√3/2)sinφ. Тогда на γ *

a = sinφi + cosφj + (√3/2)sinφk,

dr = (-sinφi + cosφj + (√3/2)cosφk)dφ,

поэтому

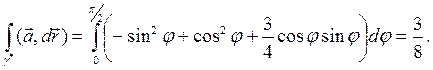
2-й способ. Контур γ* взаимно-однозначно проектируется на ось OY. Опустим перпендикуляры из точек контура на эту ось. Они образуют гладкую поверхность, граница которой состоит, кроме γ*, еще из ломаной CDOB. Используя формулу Стокса (6.5.17) и тот факт, что rot а = 0, получа­ем

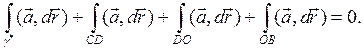
На ОВ a = xj, dr = idx и (a, dr) = 0 и .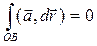

Аналогично 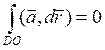. Поэтому

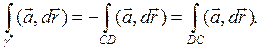
На DC a = і + zk, dr = kdz, поэтому

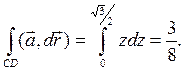
Таким образом, как и ранее,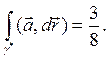

Дата добавления: 2014-11-20