Потенциальные и соленоидальные поля

Все поля в этом пункте считаются непрерывно дифференцируемыми.

Поле а в Ω называют безвихревым, если

rot а = 0 в Ω.

Поле а в Ω называю т потенциальным, если существует на Ω скалярное поле и такое, что

a = grad u. (6.5.19)

Функцию и называют потенциалом поля а.

Для потенциальности поля а в Ω необходимо и достаточно, чтобы его циркуляция по любому кусочно-гладкому замкнутому контуру равнялась ну­лю:

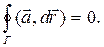
Если это условие выполнено, то потенциал поля определяется интегрированием полного дифференциала по формуле

(6.5.20)

где M₀ - фиксированная точка Ω, а интеграл вычисляется по любой кусочно-гладкой кривой, соединяющей М₀ и М. Условие

rot a = 0 (6.5.21)

необходимо для потенциальности поля, но, вообще говоря, не достаточно.

Если область Ω односвязная, то условие (6.5.21) достаточно для по­тенциальности поля. Говорят, что область Ω односвязная, если любой при­надлежащий ей кусочно-замкнутый контур можно стянуть в точку этой об­ласти так, чтобы во всех промежуточных положениях при стягивании контур будет оставаться в Ω (в этом случае говорят, что любой замкнутый контур гомотопен точке). Например, всякая выпуклая область односвязная.

В односвязной области безвихревое поле - потенциальное.

Поле а в Ω называют соленоидальным, если для любой области G Ω с кусочно-гладкой границей Ω поток поля а через эту границу равен нулю, то есть

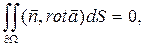(6.5.22)

где n - внешняя нормаль к Ω.

Для соленоидальности поля необходимо и достаточно, чтобы

div a = 0 в Ω (6.5.23)

Векторное поле А называют векторным потенциалом поля а, если а = rot A.

Условие (6.5.23) необходимо, но, вообще говоря, не достаточно для существования векторного потенциала.

Любое гладкое поле а в Ω является суммой потенциального и соленои-дального полей (теорема Гельмгольца).

Потенциальное соленоидальное поле называется гармоническим (тео­рема Лапласа). В односвязной области Ω поле а, у которого

rot a = 0, div a = 0,

гармонично.

Раздел 7. Числовые и функциональные ряды. Ряды Фурье.

Дата добавления: 2014-11-20