Тема 7.1. Числовые ряды. Ряды с положительными членами. Ряды с членами любого знака. Знакочередующиеся ряды

Интеграл Фурье

Учебники: [16, гл. 3, § 2, п. 6, гл. 17, § 1, пп. 1,2].

Аудиторная работа: [3, №№ 2737, 2739, 2749, 2755, 2756, 2762, 2764, 2766, 2768, 2769, 2792, 2794, 2997], [7, кн. 2, §§ 1 - 3, Ms 38, 40, 41, 42, 44, 45, 51, 54, 55, 59, 61, 65, 70, 74, 77, 81, 84, 87, 89, 91], [20, ч. 2, гл. 12, § 1, №№ 12.19, 12.21, 12.23, 12.26, 12.31, 12.32, 12.36, 12.40, 12.43, 12.49, 12.51, 12.25, 12.90, 12.91, 12.95, 12.104], [34, гл. 3.1, №№ 2.1, 2.4, 3.10 - 3.14, 4.1 -4.4, 5.1 - 5.4, 7.4, 7.5, 7.7, 7.22].

Самостоятельная работа: [3, №№ 2738, 2741, 2745, 2750, 2753, 2758, 2761, 2763, 2765, 2767, 2770, 2790, 2791, 2793, 2795, 2798], [7, кн. 2, §§ 1 - 3, №№ 39, 46 - 48, 50, 53, 57, 63, 64, 68, 71, 73, 75, 78, 82, 88, 92], [20, ч. 2, гл. 12, § 1, №№ 12.22, 12.24, 12.27, 12.34, 12.35, 12.41, 12.42, 12.50, 12.55, 12.60, 12.92, 12.93, 12.99, 12.102], [34, гл. 3.1, №№ 1.2, 1.11,2.5-2.6,3.15-3.20,4.5 -4.8, 5.5-5.8, 6.11, 6.13, 6.17, 7.1, 7.3, 7.8, 7.15, 7.18, 7.20].

Числовым рядом называется выражение

(7.1.1)

где числа а_n, n = 1,2,... - члены ряда.

Выражение S_n = a₁ + а₂ +... + а_n называется частичной суммой ряда (7.1.1), а сам ряд называется сходящимся, если существует . Число S называется суммой ряда.

Среди достаточных признаков сходимости рядов с положительными членами наиболее распространенные признаки сравнения (общий и предель­ный), признак Даламбера, признаки Копій (радикальный и интегральный).

Следует отметить, что сравнение рядов, которые исследуются на схо­димость, как правило, производится при помощи рядов:

а) (геометрическая прогрессия, которая сходится при |q|<1 и
расходится при |q| ≥ 1);

б) (расходящийся гармонический ряд);

в) (обобщенный гармонический ряд, который сходится при р > 1 и расходится при р ≤ 1).

При применении признаков Даламбера и радикального Коши вычисляются пределы: и .

Если хотя бы один из пределов равен единице, то и второй будет равен единице. Таким образом, если признак Даламбера (радикальный признак Коши) не дает ответа на вопрос о сходимости ряда, то и радикальный при­знак Коши (признак Даламбера) применять не имеет смысла.

Среди признаков сравнения, Даламбера, радикального и интегрального Коши наиболее эффективным является интегральный признак Коши. Поэто­му, если другие признаки не позволяют решить вопрос о сходимости или расходимости числового ряда с положительными членами, то следует при­менить интегральный признак Коши.

Пример 7.1.1. Исследовать на сходимость ряд , используя:

1) признак Даламбера;

2) интегральный признак Коши.

1) По условию 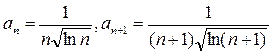, поэтому и признак Даламбера не дает ответа на вопрос о сходимости ряда.

2) Члены а_n ряда, заданного по условию, положительны и убывают. Поэтому вместо ряда можно исследовать на сходимость несобственный интеграл , где .

Несобственный интеграл расходится, следовательно, и предложенный ряд расходится.

Если ряд (7.1.1) имеет произвольные члены а_n>0 или а_n<0, n = 1,2,..., то для исследования вопроса о сходимости применяют утверждение: если , то ряд с членами произвольного знака сходится. В этом случае ряд называется абсолютно сходящимся. Для знакочередующихся ря­дов

(7.1.2)

при выяснении вопроса о сходимости применяется достаточный признак сходимости Лейбница, а именно: если для ряда (7.1.2) и a_n > a_n+1, n ≥ 1, торяд сходится.

Этот признак не гарантирует абсолютную сходимость. Если абсолют­ной сходимости нет, а признак Лейбница выполняется, то ряд (7.1.2) называ­ется условно сходящимся.

Пример 7.1.2. Исследовать на сходимость числовой ряд

.

Решение. Приведенный ряд - это знакочередующийся числовой ряд (7.1.2), для которого . Исследуем этот ряд на абсолютную сходимость по признаку Даламбера

.

Поэтому ряд сходится абсолютно и, следовательно, условно.

Пример 7.1.3. Исследовать на сходимость числовой ряд

.

Решение. Ряд вида (7.1.2), . Абсолютная сходимость отсутствует, т. к. ряд с общим членом является обобщенным гармоническим рядом с параметром р = 2/3 < 1, т. е. расходящимся рядом.

Проверим условную сходимость по признаку Лейбница:

.

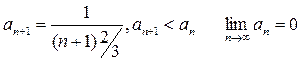По признаку Лейбница ряд сходится.

Замечание. Если не выполняется необходимое условие сходимости ря­да , то дальнейшие исследования проводить не нужно, т. к. ряд расходится.

Пример 7.1.4. Исследовать на сходимость ряд .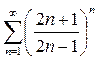

Решение. Проверим необходимое условие сходимости:

.

.

Необходимое условие сходимости ряда не выполняется, поэтому ряд расхо­дится.

Дата добавления: 2014-11-20