Решение. а) Общий член ряда имеет вид (см

а) Общий член ряда имеет вид 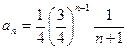(см. формулу (7.1.1)).

Поскольку , а ряд 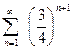сходится, то по признаку сравнения исходный ряд также сходится.

б) Предложенный ряд – это знакочередующийся ряд (7.1.2), для которого

Исследуем ряд на абсолютную сходимость, используя предельный признак сравнения.

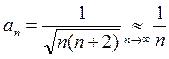; ряд – расходится (гармоничный ряд), 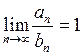. Ряды 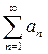и 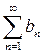ведут себя одинаково. Следовательно, ряд 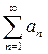расходится и абсолютной сходимости нет.

Условную сходимость проверим по признаку Лейбница:

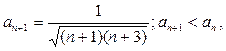
т.е. члены ряда образуют убывающую последовательность. Поэтому по признаку Лейбница ряд 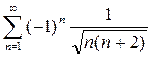условно сходится.

9. Определить область сходимости функционального ряда .

Решение. Данный ряд – степенной ряд. Радиус сходимости находим по формуле (7.2.1):

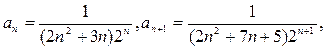
Таким образом, ряд сходится, если |x-4| < 2 или -2<x-4<2, 2<x<6.

Проверим сходимость в граничных точках интервала сходимости:

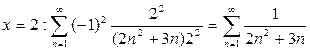
- ряд абсолютно сходится;

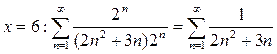
- ряд абсолютно сходится.

Ответ: функциональный ряд сходится при всех значениях xє[2;6].

10. Найти сумму ряда .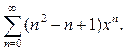

Решение. Обозначим сумму исходного ряда S(x). Прежде всего необходимо найти область сходимости исходного ряда. Предложенный ряд – это степенной ряд, радиус сходимости R=1 (см. решение примера 9). Поэтому |x|<1 (при х =±1 ряд расходится). Таким образом, сумма исходного ряда может быть найдена лишь при значениях хє(-1;1).

Преобразуем исходный ряд к виду

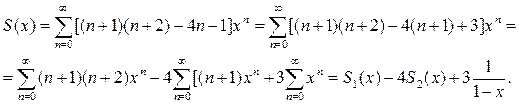
Последний ряд просуммирован сразу, т.к. является суммой бесконечно убывающей геометрической прогрессии с первым членом b₁ = 1 и знаменателем прогрессии q(x)=x, |q(x)|<1.

Вычислим S₂(x), предварительно проинтегрировав соответствующий ряд .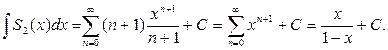

Отсюда .

Вычислим S₁(x), предварительно дважды проинтегрировав ряд

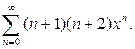
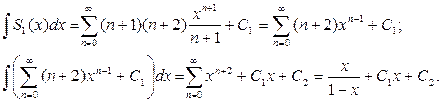
Откуда

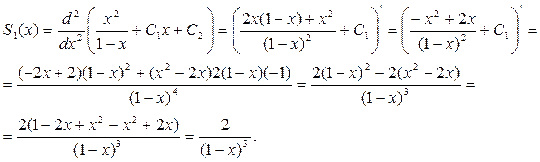
Таким образом,

11. Вычислить интеграл 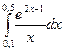с точностью до ε=10^-3.

Решение. Задача, аналогичная данной, рассмотрена в примере 7.2.4 (см.тему 7.2). Оценку остатка ряда (остаточный член) следует производить по формуле , т.к. в данном случае будет получен числовой ряд с положительными членами.

12. Функцию 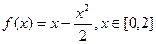разложить в ряд Фурье по косинусам. Построить график суммы ряда.

Решение. В промежутке [-2,0) продолжим функцию f(x) четным образом. Ряд Фурье будет иметь вид

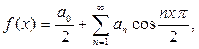
т.к. l = 2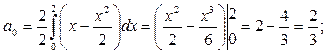

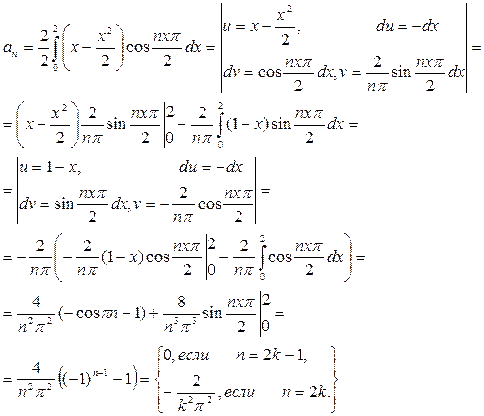
Таким образом, .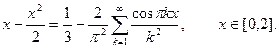

График суммы ряда имеет вид (рис. Д.7.1).

13. Найти косинус-преобразование Фурье функции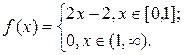

Решение. Функцию f(x) продолжим на отрицательную полуось четным образом и косинус-преобразование Фурье будем искать для функции

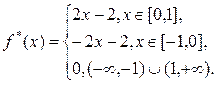
По формуле (7.4.7) находим

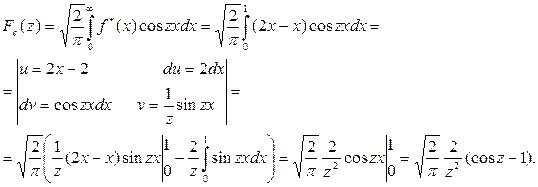
14. Найти первые три отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения .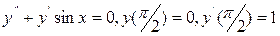

Решение дифференциального уравнения ищем в идее

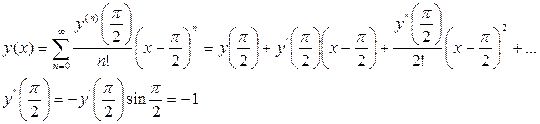
Таким образом,

.

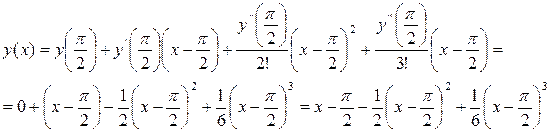Дата добавления: 2014-11-20