Условия устойчивости линейных систем автоматического управления

Покажем, как на основе изложенного выше определения устойчивости А. М. Ляпунова можно найти условия устойчиво­сти линейных (линеаризованных) систем автоматического уп­равления.

Дифференциальное уравнение линейной системы автома­тического управления, записанное для регулируемой выход­ной величины х(t) при наличии управляющего воздействия g(t),имеет вид

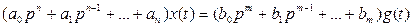(3.22)

где а₀,а,,..., а_nи b₀, b₁..., b_m— постоянные коэффициенты, а р= d/dt — оператор дифференцирования.

Изменение регулируемой величины х(t)при произвольном внешнем воздействии g(t) представляет собой решение урав­нения (3.22):

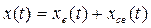(3.23)

В (3.23) первое слагаемое 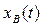— вынужденная составляю­щая, имеющая тот же характер, что и правая часть уравнения (3.21). Она определяется как частное решение неоднородного дифференциального уравнения (3.21) с правой частью:

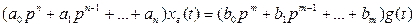(3.24)

Второе слагаемое 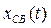— свободная (переходная) составляю­щая, которая определяется общим решением однородного диф­ференциального уравнения (3.21) без правой части:

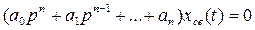(3.25)

Обычно в теории автоматического управления интересуют­ся устойчивостью вынужденной составляющей 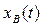переход­ного процесса. Поэтому за невозмущенное движение системы необходимо принять вынужденную составляющую переходно­го процесса 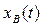.Тогда возмущенным движением будет любое возможное в системе изменение регулируемой величины х(t), а отклонением или вариацией — свободная составляющая

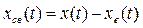(3.26)

Возмущениями, по А. М. Ляпунову, являются начальные значения 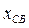,которые возникли в момент t = t₀под действи­ем внезапно подействовавших дополнительных внешних сил, т. е. начальные значения 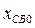.Дифференциальными уравне­ниями возмущенного движения первого приближения в дан­ном случае будут уравнения (3.25).

В соответствии с определением устойчивости по А. М. Ляпу­нову система будет асимптотически устойчивой, если с тече­нием времени при t → ∞ свободная составляющая будет стре­миться к нулю, т. е. . Чтобы найти эту составляю­щую, необходимо решить дифференциальное уравнение (3.25):

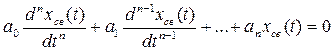(3.27)

Решение уравнения (3.27) находят как 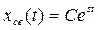. Дифференцируя это выражение nраз и подставляя в (3.27), после сокращения на общий множитель 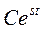получаем

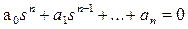(3.28)

Полученное алгебраическое уравнение (3.28) называют характеристическим уравнением. Его корни s₁, s₂,.... s_nбудут определять характер переходного процесса в системе. Нетрудно заметить, что по своему виду левая часть уравнения (3.28) совпадает с дифференциальным оператором при выход­ной величине в уравнении (3.22), поэтому характеристичес­кое уравнение получают обычно, приравнивая к нулю диф­ференциальный оператор привыходной величине в исходном дифференциальном уравнении(3.22), т. е.

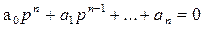(3.29)

Следует заметить, одна­ко, что в характеристичес­ком уравнении (3.29), р = sозначает уже не сим­вол дифференцирования, а некоторое комплексное число.

Решение характеристи­ческого уравнения степени nсодержит nкорней. Кор­ни характеристического уравнения обыкновенного линейного дифференциаль­ного уравнения с постоян­ными коэффициентами могут быть вещественными, комплекс­ными попарно сопряженными, мнимыми попарно сопряжен­ными, нулевыми. В общем случае

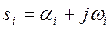(3.30)

На рис. 3.3 показаны возможные положения корней в ком­плексной плоскости корней s:

; ; ; ; ;

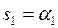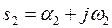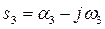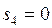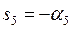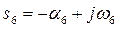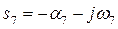; . (3.31)

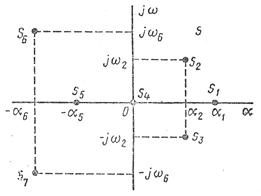
Рис.3.3. Возможные положения корней в ком­плексной плоскости корней s.

Если все корни разные, то их называют простыми. Если среди корней есть одинаковые, то их называют кратными.

Обычно корни с отрицательными вещественными частями принято называть левыми,поскольку они в комплексной пло­скости корней расположены слева от мнимой оси, а корни с положительными вещественными частями — правыми корнями.

Условие устойчивости линейной системы формулируется следующим образом: для того чтобы линейная система была асимптотически устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения (3.29) были левыми.

Указанное условие устойчивости легко пояснить, рассматривая решение однородного уравнения (3.27), которое при отсутствии крат­ных корней имеет вид

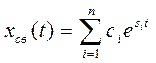, (3.32)

где 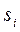— корни характеристического уравнения (3.29); 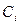— постоян­ные интегрирования, определяемые из начальных условий.

Заметим, что корни характеристического уравнения 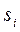зависят только от вида левой части дифференциального уравнения (3.22) ли­нейном системы. Постоянные интегрирования 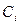зависят и от вида правой ее части, поэтому быстрота затухания и форма переходного про­цесса определяются как левой, так и правой частями исходного дифференциального уравнения (3.22). Однако, поскольку в понятие устойчивости входит только факт наличии или отсутствия затухания переход­ного процесса, устойчивость линейной системы не зависит от вида правой части дифференциального уравнения (3.22) и определяется только характеристическим уравнением (3.29).

При составлении (3.22) предполагалось, что внешние возмущаю­щие воздействия отсутствуют. Если записать дифференциальные урав­нения движения системы относительно возмущающего воздействия, то в этом случае левая часть (3.22) остается без изменения, а правая будет иметь другой вид. Так как характер переходного процесса в линейной системе определяют только по виду левой части дифференциального уравнения (3.22), то для определения качественной картины переход­ных процессов практически безразлично, записать ли исходное диффе­ренциальное уравнение для управляющего или возмущающего воздей­ствия.

Вещественным корням характеристического уравнения 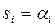в (3.32) соответствуют слагаемые, представляющие собой экспоненты .

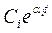Очевидно, что отрицательным (левым) корням 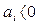соответст­вуют затухающие экспоненты (рис. 3.4 а).Положительным (правым) корням 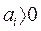— возрастающие экспоненты (рис. 3.4 б)и при пуле­вых корнях 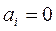слагаемые представляют собой прямые, параллель­ные оси времени (рис. 3.4 в).

Комплексные корни характеристического уравнения всегда бы­вают попарно сопряженным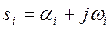и: и 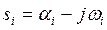. Слагаемые, определяемые этими корнями в (3.32), могут быть при

использовании известной формулы Эйлера:

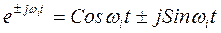(3.33)

представлены в виде

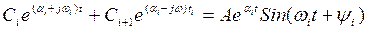, (3.34)

где A_iи ψ_i - новые постоянные.

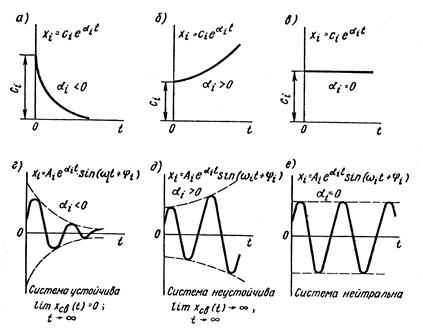
Рис. 3.4. Виды решений однородного уравнения

В этом случае при 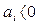получаются затухающие колебания (рис. 3.4 г),при 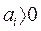— расходящиеся колебания (рис. 3.4 д)и при 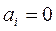— незатухающие колебания (рис. 3.4 е). Для устойчивости и в этом случае необходимо выполнение условия 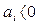. В самом об­щем случае среди корней характеристического уравнения (27) могут быть кратные корни. Если имеется rкратных корней 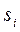, то в (29) появятся слагаемые вида

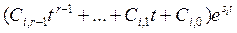. (3.35)

Если корень 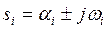имеет отрицательную вещественную часть 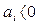, то множитель 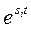будет с течением времени убывать. Множитель в скобках неограниченно растет, поэтому мы имеем неопределенность ∞0. Однако известно, что 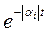быстрее стремится к нулю, чем выражение 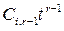возрастает,поэтому при 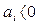эта группа слагае­мых с течением времени также стремится к нулю.

Таким образом, видно, что в самом общем случае для устойчивости линейной системы необходимо и достаточно, чтобы все корни характе­ристического уравнения (3.29) были левыми.

Если хотя бы один корень окажется справа от мнимой оси, то система будет неустойчивой. Таким образом мнимая ось представляет собой граничную линию в плоскости корней, за которую не должны

переходить корни характе­ристического уравнения. Вся левая полуплоскость представляет собой при этом область устойчивости.

Превращение устойчивой системы в неустойчивую произойдет в том

случае, если хотя бы один вещественный корень или пара комплексных

корней перейдет из левой полуплоскости в правую. Границей перехода

будет так называемая граница устойчивости системы. Система будет

находиться на границе устойчивости при наличии:

1. Нулевого корня;

2. Пары чисто мнимых корней;

3. Бесконечного корня.

Во всех трех случаях предполагается, что все остальные корни имеют

отрицательные вещественные части.

В первом случае вещественный корень попадает на границу устойчивости (ось Jm) в начале координат, то есть выполняется условие 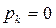.Это означает, что в характеристическом уравнении будет отсутствовать свободный член . Дифференциальное уравнение в этом случае имеет вид:

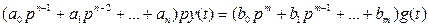(3.36)

и система будет устойчивой не относительно регулируемой величины y

а относительно ее скорости изменения py. Величина же отклонения

регулируемой величины может принимать произвольные значения. Такую

систему называют нейтрально устойчивой, имея в виду ее безразличие к

значению самой регулируемой величины.

На границе устойчивости второго типа, которая называется колебательной, два корня попадают на ось Jm. Система в этом случае будет

иметь незатухающие гармонические колебания с постоянной амплитудой.

Вещественный корень может попасть из левой части в правую,

проходя через бесконечность. В этом случае соответствующее слагаемое 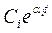обращается в нуль, что соответствует понижению порядка

дифференциального уравнения на единицу. Это будет при .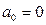

Граница устойчивости третьего типа встречается сравнительно редко

Вычисление корней просто лишь для характеристического уравнения первой и второй степеней. Существуют общие вы­ражения для корней уравнений третьей и четвертой степеней, но эти выражения громоздки и практически малопригодны. Общие выражения для корней уравнений более высоких сте­пеней вообще невозможно написать через коэффициенты характеристического уравнения. Поэтому важное значение при­обретают правила, которые позволяют определять устойчи­вость системы без вычисления корней. Эти правила называют критериями устойчивости. С помощью критериев устойчиво­сти можно не только установить, устойчива система или нет, но и выяснить, как влияют на устойчивость те или иные пара­метры и структурные изменения в системе.

Необходимым (но недостаточным) условием устойчивости системы

является положительность всех коэффициентов характеристического уравнения. Это значит, что при положительности всех коэффициентов

система может быть устойчивой, но не исключена возможность

неустойчивости системы. Если же не все коэффициенты характеристического уравнения положительны, то система наверняка

неустойчива и никаких дополнительных исследований устойчивости не

требуется.

Критерии устойчивости могут быть разделены на алгебраи­ческиеи частотные. С математической точки зрения все критерии устойчивости эквивалентны, однако целесообразный вы­бор того или иного критерия устойчивости при решении кон­кретных задач позволяет провести исследование устойчивости наиболее простым путем.

Дата добавления: 2014-11-20