Критерий устойчивости Гурвица

В 1895 г. немецким мате­матиком А. Гурвицем был разработан алгебраический крите­рий устойчивости в форме определителей, составляемых из коэффициентов характеристического уравнения системы.

Из коэффициентов характеристического уравнения (3.37) строят сначала главный определитель Гурвица:

a₁ a₃ a₅ a₇ … 0

—

a₀ a₂ a₄ a₆ … 0

——

Δ_n = 0 a₁ a₃ a₅ … 0 (3.46)

———

0 a₀ a₂ a₄ … 0

……………………

0 0 0 0 a_n

по следующему правилу: по главной диагонали определите­ля слева направо выписывают все коэффициенты характерис­тического уравнения от а₁ до а_n в порядке возрастания индек­сов. Столбцы вверх от главной диагонали дополняют коэффи­циентами характеристического уравнения с последовательно возрастающими индексами, а столбцы вниз — коэффициента­ми с последовательно убывающими индексами. На место коэф­фициентов с индексами больше n (n— порядок характеристи­ческого уравнения) и меньше нуля проставляют нули.

Отчеркивая в главном определителе Гурвица, как показано пунктиром, диагональные миноры, получаем определители Гурвица низшего порядка:

a₁ a₃ a₁ a₃ a₅ a₁ a₃ a₅ …

Δ₁ = a₁ Δ₂ = a₀ a₂ Δ₃ = a₀ a₂ a₄ Δ_k = a₀ a₂ a₄ …

0 a₁ a₃ 0 a₁ a₃…

… …

a_k

(3.47)

Номер определителя Гурвица определяется номером коэф­фициента по диагонали, для которого составляют данный опре­делитель. Критерий устойчивости Гурвица формулируется следующим образом: для того чтобы система автоматическо­го управления была устойчива, необходимо и достаточно, чтобы все определители Гурвица имели знаки, одинаковые со зна­ком первого коэффициента характеристического уравнения 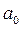, т. е. при 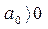были положительными.

Таким образом, при 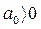для устойчивости системы необходимо и достаточно выполнения следующих условий:

a₁ a₃ a₁ a₃ a₅

Δ₁ = a₁ > 0 Δ₂ = a₀ a₂ > 0 Δ₃ = a₀ a₂ a₄ > 0

0 a₁ a₃

………………………………………………………………………………..

a₁ a₃ a₅ … 0

a₀ a₂ a₄ … 0

Δ_n = 0 a₁ a₃ … 0

…………..

0 0 0 …. A_n (3.48)

Раскрывая, например, определители Гурвица для характе­ристических уравнений первого, второго, третьего и четвер­того порядков, можно получить следующие условия устойчи­вости:

1) для уравнения первого порядка (n = 1)

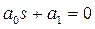(3.49)

условия устойчивости

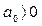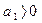; ; (3.50)

2) для уравнения второго порядка (n= 2)

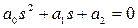(3.51)

условия устойчивости

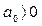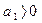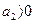; ; (3.52)

3) для уравнения третьего порядка (n = 3)

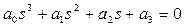(3.53)

условия устойчивости

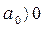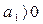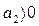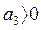; ; ; ; (3.54)

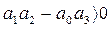; (3.55)

4) для уравнения четвертого порядка (n=4) 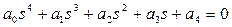(3.56)

условия устойчивости

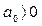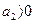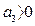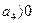; ; ; ; (3.57)

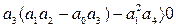; (3.58)

5) для уравнения пятого порядка (n=5) 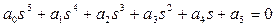(3.59)

условия устойчивости

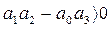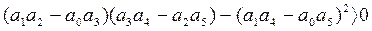, (3.60)

Таким образом, необходимым и достаточным условием ус­тойчивости для систем первого и второго порядков является положительность коэффициентов характеристического уравне­ния. Для уравнения третьего и четвертого порядков кроме по­ложительности коэффициентов необходимо соблюдение допол­нительных неравенств (3.55) и (3.58).

При n ≥ 5 число подобных дополнительных неравенств возрастает, процесс раскрытия определителей становится до­вольно трудоемким и громоздким. Поэтому критерий устой­чивости Гурвица обычно применяют при n ≤ 4. При n ≥5 це­лесообразно применять критерий устой­чивости Льенара — Шипара, либо при использовании крите­рия устойчивости Гурвица переходить к численным методам с использованием компъютера.

В последнем столбце главного определителя Гурвица отличен от нуля только один коэффициент 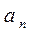,поэтому

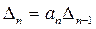(3.61)

Из (3.61), видно, что при а_n > 0 для проверки устойчивости системы достаточно найти только определители Гурвица от Δ₁до Δ_n-1. Если все определители Гурвица низшего порядка положительны, то система находится на границе устойчиво­сти, когда главный определитель равен нулю:

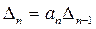(3.62)

Последнее равенство возможно в двух случаях: 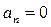или 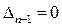. В первом случае система находится на границе апериодической устойчивости (один из корней характеристи­ческого уравнения равен нулю); во втором случае — на гра­нице колебательной устойчивости (два комплексно-сопряжен­ных корня характеристического уравнения находятся на мни­мой оси).

Используя критерий Гурвица, можно при заданных пара­метрах системы принять за неизвестный какой-либо один параметр (например, коэффициент усиления, постоянную вре­мени и т. д.) и определить его предельное (критическое) зна­чение, при котором система будет находиться на границе ус­тойчивости.

Критерий Гурвица можно получить из критерия Рауса, поэтому иногда критерий Гурвица называ­ют критерием Рауса — Гурвица.

Пример 1. Пусть задано характеристическое уравнение системы

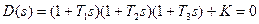, (3.63)

где К— коэффициент усиления разомкнутой системы;

Т₁, Т₂, Т₃— постоянные времени отдельных динамических звеньев системы. Найдем, пользуясь критерием Гурвица, предельное значение коэффициента уси­ления разомкнутой системы К_КРкак функцию постоянных времени Т₁, Т₂,Т₃.

Перепишем характеристическое уравнение в виде

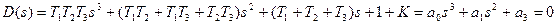(3.64)

где: , , 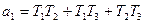, 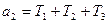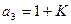. (3.65)

Согласно критерию устойчивости Гурвица, система третьего поряд­ка будет устойчива, если выполняются следующие неравенства:

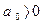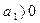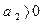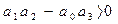, , , , . (3.66)

В данном случае все коэффициенты характеристического уравне­ния положительны, поэтому система будет устойчива, если

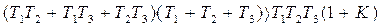. (3.67)

Последнее неравенство можно переписать в виде

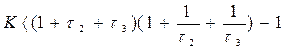, (3.68)

где: , 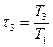. (3.69)

Предельное (критическое) значение коэффициента усиления, при котором система будет находиться на границе устойчивости, равно

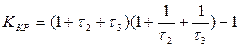. (3.70)

Из последнего выражения следует, что предельный коэффициент усиления системы определяется не абсолютными значениями постоянных времени динамических звеньев, а их относительными значениями. Чем более резко отличаются постоянные времени друг от друга, тем больше К_КР. В частном случае, когда τ₂ = τ ₃= 1, т. е. Т₁ = T₂ = T₃,зна­чение К_КР минимально и равно всего лишь К_КР = 8.

Пример 2. Исследовать устойчивость системы автоматического регулирования (рис. 3.5) с помощью критерия Рауса - Гурвица:

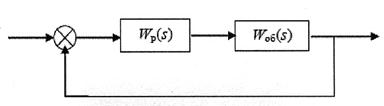
Рис. 3.5. Структурная схема системы автоматического регулирования

Заданы следующие исходные данные; передаточные функции объекта и регулятора

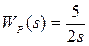
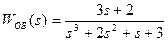(3.71)

Для исследования устойчивости систем автоматического регулирования с помощью критерия Рауса - Гурвица необходимо знать дифференциальное или характеристическое уравнение системы. Знаменатель передаточной функции всегда представляет собой характе­ристический полином, поэтому необходимо, прежде всего, записать передаточную функцию замкнутой одноконтурной системы (рис. 3.5):

(3.72)

Характеристическое уравнение определяется путем приравнивания к нулю знаменателя передаточной функции замкнутой системы

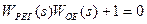(3.73)

с учетом конкретных значений передаточных функций объекта и регулятора получим

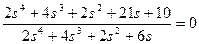(3.74)

откуда характеристическое уравнение запишется в виде

(3.75)

Задачу будем решать с использованием формулировки критерия устойчивости по Гурвицу. Для этого необходимо из коэффициентов характеристического уравнения составить главный определитель Гурвица. Порядок определителя соответствует порядку характеристи­ческого уравнения. Из этого определителя составляются диагональные миноры, которых должно быть n — 1.

Система автоматического управления будет устойчивой тогда и только тогда, когда все диагональные миноры главного определителя будут положительны.

Для нашей задачи главный определитель Гурвица имеет вид

4 21 0 0

2 2 10 0

0 4 21 0 (3.76)

0 2 2 10

Вычислим последовательно диагональные миноры:

Δ₁ = 4 > 0 Δ₂ = 8 – 42 = - 34 < 0 (3.77)

Δ₃ = 4*(42 - 40) - 21*42 = - 874 < 0 Δ₄ = - 874*10 = - 8740 < 0 (3.78)

Все диагональные миноры отрицательны, следовательно, система неустойчива. Следует отметить, что для исследования устойчивости не обязательно вычислять все миноры. Если при вычислении миноров получают, что его значение отрицательно, дальнейшие расчеты можно прекратить и сделать вывод, что система неустойчива.

Дата добавления: 2014-11-20