
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие устойчивости 1 страница
|
|
|
|
Вариант 10-Вариант
Вариант 8-Вариант
Вариант 6-Вариант
Вариант 4-Вариант
Вариант 2-Вариант
Вариант
Вариант
ВАРИАНТ
ВАРИАНТ
ВАРИАНТ
ВАРИАНТ
ВАРИАНТ
ВАРИАНТ
1. Егер полюс координаталар басында жатса, ал поляр oci абцисалар
өсімен беттессе,онда А(3,4)координаталары қандай болады?
A) 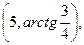
B) 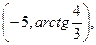
C) 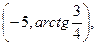
D) 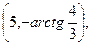
E) 
2. Центр1 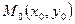 нуктесінде болатын түзулер шоғының теңдеуі қандай болады?
нуктесінде болатын түзулер шоғының теңдеуі қандай болады?
А) 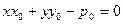
В) 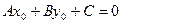


С) 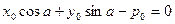
D) 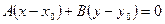
Е) 
3. a = 3 i- 4j + 5к векторы бершген. Осы вектордың абсциссасынкөрсетіңіз:
А) 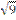
В) 5.
С) 6.
D) -3.
Е) 3.
F) 6
4. Лопиталь ережесін қолданып функцияның шегін табыңыз 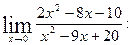
А) 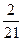
B) 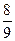
C) 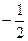
D) 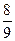
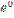
E) 2
F) 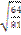
G)12
5. Лопиталь ережесін қолданып функцияның шегін табыңыз 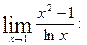
А) 2
B) -1
C) 0
D) 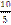
E) -2
F) 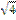
G)1
6. 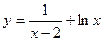 функциясының анықталу облысын табыңыз:
функциясының анықталу облысын табыңыз:
А) 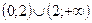
B) 
C) 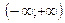
D) 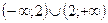
E) 
7. Егер қандай бір аралықта 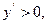 онда функция
онда функция 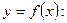
А) өседі
B) тұрақты
C) дөңес
D) кемиді
E) ойыс
8. 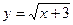 функциясының
функциясының 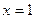 нүктесіндегі туындысының мәні:
нүктесіндегі туындысының мәні:
А) 2
B) 0,25
C) 0,5
D) -1
E) 
F)5
G) 
9. 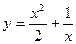 функциясының максимумдарын табыңыздар:
функциясының максимумдарын табыңыздар:
А) 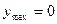
B) 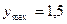
C) 
D) максимум жоқ
E) 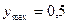
10. 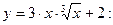 функциясының туындысын тап:
функциясының туындысын тап:
А) 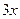
B) 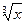
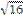
C) 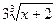
D) 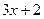
E) 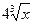
F)5
G) 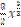
11. 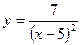 функциясының туындысы тең:
функциясының туындысы тең:
А) 0
B) 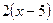
C) 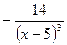
D) 
E) 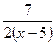
12. 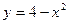 параболасымен және
параболасымен және 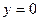 түзуімен шектелген фигураның ауданын есептеңіз:
түзуімен шектелген фигураның ауданын есептеңіз:
А) 16
B) 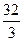
C) 
D) 1
E) 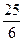
F)5
G) 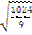
13. 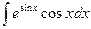 интегралын табу үшін мақсатқа сәйкес алмастыруды көрсетіңіз:
интегралын табу үшін мақсатқа сәйкес алмастыруды көрсетіңіз:
А) 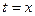
B) 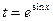
C) 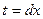
D) 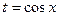
E) 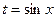
14. 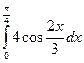 есептеңіз:
есептеңіз:
А) 2
B) 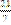
C) 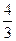
D) -3
E) 3
F) 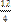
G) 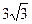
15. 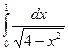 есептеңіз:
есептеңіз:
А) 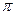
B) 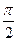
C) 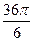
D) 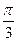
E) 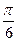
F) 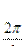
16. 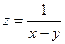 функциясының толық дифференциалы тең:
функциясының толық дифференциалы тең:
А) 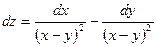
B) 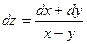
C) 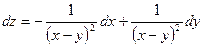
D) 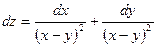
E) 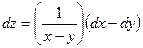
17. Теңдеулердің қайсысы айнымалдары ажыратылатын теңдеуге жатады?
А) 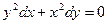
B) 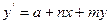
C) 
D) 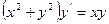
E) 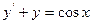
18. 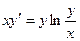 теңдеуін шешу үшін қолданылатын тәсіл:
теңдеуін шешу үшін қолданылатын тәсіл:
А) Тұрақтыны түр өзгерту тәсілі
B) Айнымалыларын бөліп алу
C) Тікелей интегралдау тәсілі
D) 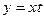 ауыстыруын жасау
ауыстыруын жасау
E) 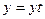 ауыстыруын жасау
ауыстыруын жасау
19. 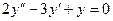 теңдеуінің мінездемелік теңдеуін құрыңыз:
теңдеуінің мінездемелік теңдеуін құрыңыз:
А) 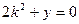
B) 
C) 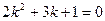
D) 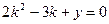
E) 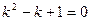
20. Жанұяда бес бала бар. Ұл туу ықтималдығы 0,5 болса, балалардың екеуден кем емес екенінің ықтималдығы тап:
А) 
B) 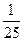
C) 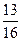
D) 0,25
E) 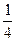
F) 
G) 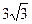
21. Дискретті кездейсоқ шама Х үлестіру заңы арқылы берілген:
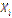
| ||||
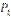
| 0.2 | 0.35 | 0.3 | 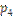
|
 табыңыз:
табыңыз:
А) 0
B) 1
C) 0,05
D) 0,15
E) 0,2
F) 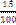
22. 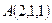 нүктесі арқылы өтетін және
нүктесі арқылы өтетін және 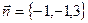 векторына перпендикуляр болатын жазықтықтың теңдеуін жазыңыз:
векторына перпендикуляр болатын жазықтықтың теңдеуін жазыңыз:
А) 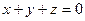
B) 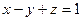
C) 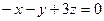
D) 
E) 
23. 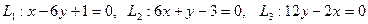 түзулері берілген. Параллель түзулерді көрсетіңіз:
түзулері берілген. Параллель түзулерді көрсетіңіз:
А)  және
және 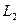
B) 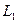 және
және 
C) 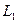 және
және 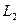
D) 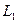 ,
, 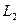 ,
,  .
.
E) Параллель түзулер жоқ.
24. 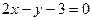 және
және  түзулерінің қиылысу нүктесі:
түзулерінің қиылысу нүктесі:
А) 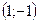
B) 
C) 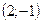
D) 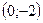
E) 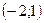
F) 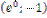
25.  векторларына салынған пирамиданың көлемі тең:
векторларына салынған пирамиданың көлемі тең:
А) 1.5
B) 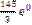
C) 3
D) 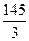
E) 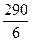
F) 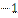
G) 2.2
1. Түзу 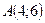 нүктесі арқылы өтеді және түзудің бұрыштық коэффициенті
нүктесі арқылы өтеді және түзудің бұрыштық коэффициенті 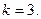 Түзудің теңдеуі мынадай түрде блады:
Түзудің теңдеуі мынадай түрде блады:
А) 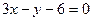
B) 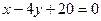
C) 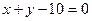
D) 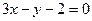
E) 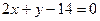
2. 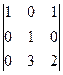 анықтауышының
анықтауышының 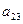 элементінің алгебралық толықтауышы
элементінің алгебралық толықтауышы 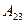 есептеңіз:
есептеңіз:
А) 1
B) -3
C) 2
D) 
E) -1
F) 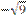
G) 2.2
3.  берілсе,
берілсе, 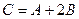 матрицасын табыңыз.
матрицасын табыңыз.
А) 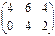
B) 
C) 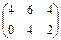
D) 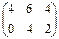
E) 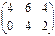
4. Лопиталь ережесін қолданып функциясының шегін табыңыз 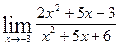 :
:
А) 7
B) 2
C) 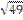
D) -2
E) 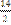
F) 5
G) 2.2
5. Шекті табыңыз 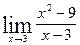 :
:
А) 0
B) 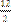
C) -3
D) 6
E) -2
F) 5
6.  функциясының анықталу облысын тап:
функциясының анықталу облысын тап:
А) 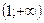
B) 
C) 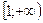
D) 
E) 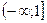
7. 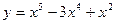 функциясының үшінші ретті туындысын табыңыз:
функциясының үшінші ретті туындысын табыңыз:
А) 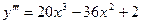
B) 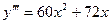
C) 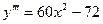
D) 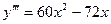
E) 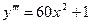
F) 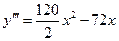
8.  функциясының өсу аралығын табыңыз:
функциясының өсу аралығын табыңыз:
А) 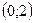
B) 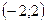
C) 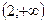
D) 
E) 
9.  функциясының
функциясының 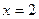 нүктесіндегі екінші ретті туындысын табыңыз:
нүктесіндегі екінші ретті туындысын табыңыз:
А) 24
B) 27
C) 15
D) 12
E) 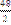
F) 5
G) 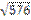
10. 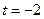 болғандығы
болғандығы 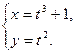 функциясының туындысын табыңыз:
функциясының туындысын табыңыз:
А) 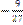
B) 0,5
C) 0
D) - 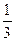
E) 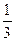
F) 6
11. 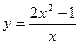 функциясының тік асимптотасы тең:
функциясының тік асимптотасы тең:
А) 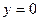
B) 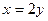
C) 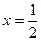
D) 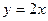
E) 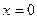
12. 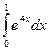 анықталған интеграл тең:
анықталған интеграл тең:
А) 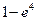
B) 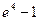
C) 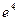
D) 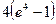
E) 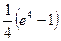
13. 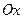 өсімен және
өсімен және 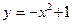 параболасымен шектелген фигураның ауданын есептеңіз:
параболасымен шектелген фигураның ауданын есептеңіз:
А) 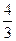
B) 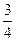
C) 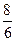
D) 4
E) 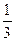
F) 5
G) 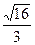
14. 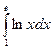 есептеңіз:
есептеңіз:
А) -1
B) 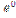

C) 1
D) 0
E) 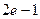
F)6
15. 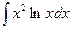 интегралда
интегралда 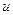 мен
мен 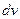 дұрыстап таңдап алыңыз
дұрыстап таңдап алыңыз
А) 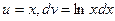
B) 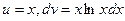
C) 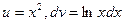
D) 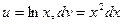
E) 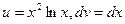
16.  функциясының айнымалыларына қатысты біртектілік дәрежесі тең:
функциясының айнымалыларына қатысты біртектілік дәрежесі тең:
А) 4
B) 3
C) 1
D) 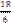
E) 0
F) 5
G) 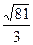
17. 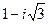 комплекс санының аргументін тап:
комплекс санының аргументін тап:
А) 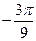
B) 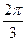
C) 
D) 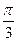
E) 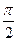
F) 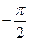
18. Екінші ретті тұрақты коэффициентті сызықтық біртекті теңдеудің фундаментальды шешімдер жүйесінің 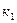 және
және 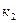 сипаттамалық теңдеудің әртүрлі түбірлері долған жағдайда берілуі:
сипаттамалық теңдеудің әртүрлі түбірлері долған жағдайда берілуі:
А) 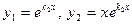
B) 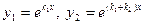
C) 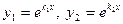
D) 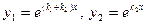
E) 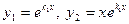
19. Берілгендердің арасындағы дифференциалдық теңдеу болатыны:
1) 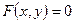
2) 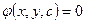
3) 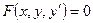
4) 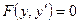
5) 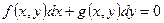
А) 3,4 B) 1,2 C) 3,5 D) 1,2,3 E) 3,4,5
20. Топтағы 15 студенттің 10 – спортшы. Кез-келген шақырылған бір студенттің спортшы екндігінің ықтималдығын табыңыз:
А) 
B) 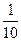
C) 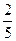
D) 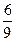
E) 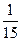
F) 5
G) 
21. Х – дискреттік кездейсоқ шама болса, онда оның математикалық күтімі тең болады:
А) 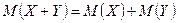
B) 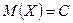
C) 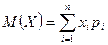
D) 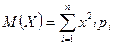
E) 
22. 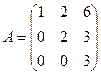 матрицасына кері матрицаны көрсет:
матрицасына кері матрицаны көрсет:
А) 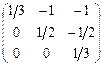 B)
B) 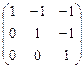 C)
C) 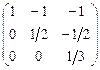
D) 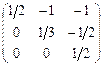 E)
E) 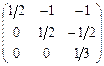
23. 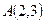 нүктесі арқылы өтетін және
нүктесі арқылы өтетін және 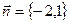 векторына перпендикуляр болатын түзудің теңдеуін жазыңыз:
векторына перпендикуляр болатын түзудің теңдеуін жазыңыз:
А) 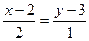
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 642; Нарушение авторских прав?; Мы поможем в написании вашей работы!