Поверхні другого порядку

3.6.1. Перетворення загального
рівняння поверхні

Означення. Поверхнею другого порядку називається геометричне місце точок простору, декартові координати яких задовольняють рівняння

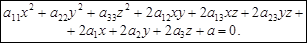(1)

Розглянемо квадратичну форму

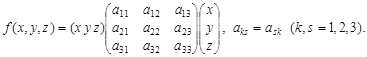(2)

Знайдемо власні числа a, b, g матриці

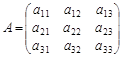
з характеристичного рівняння

.

Розглянемо ортонормовану систему власних векторів матриці А:

Заміною змінних

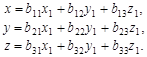(3)

Квадратична форма (2) перетворюється на квадратичну форму

.

Заміною змінних (3), яка визначає поворот простору, рівняння (1) перетворюється до простішого вигляду:

(4)

Надалі розрізнятимемо три випадки.

І. Усі коефіцієнти a, b, g відмінні від нуля.

ІІ. Два коефіцієнти a, b відмінні від нуля, а один з коефіцієнтів, наприклад g, дорівнює нулю.

ІІІ. Два коефіцієнти дорівнюють нулю, наприклад a та b, а g ¹ 0.

У випадку І переходом до нової системи координат

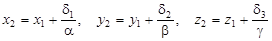
дістанемо рівняння поверхні

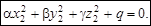(5)

У випадку ІІ перейдемо до нових координат:

.

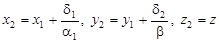Тоді рівняння (4) набере вигляду

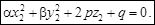(6)

У випадку ІІІ, скориставшись заміною змінних

,

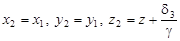перетворимо рівняння (4) так:

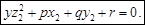(7)

Далі розглянемо докладніше поверхні, задані рівняннями (5) – (7). Наведемо рівняння та графічні зображення всіх можливих поверхонь другого порядку.

3.6.2. Поверхні у випадку І

Наведемо приклади поверхонь, які визначаються частинними випадками рівняння (5).

1. — еліптичний конус (рис. 3.55).

При а = b маємо круговий конус.

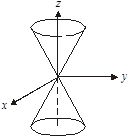
Рис. 3.55

2. 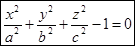— еліпсоїд (рис. 3.56).

Рис. 3.56

3. 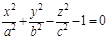— однопорожнинний гіперболоїд (рис. 3.57).

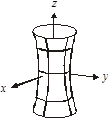
Рис. 3.57

4. — двопорожнинний гіперболоїд (рис. 3.58)

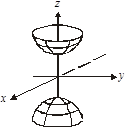
Рис. 3.58

3.6.3. Поверхні у випадку ІІ

Розглянемо частинні випадки рівняння (6).

1. 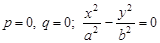— дві площини, що перетинаються (рис. 3.59).

Рис. 3.59

2. — еліптичний циліндр
(рис. 3.60).

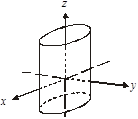
Рис. 3.60

3. 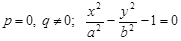— гіперболічний циліндр
(рис. 3.61).

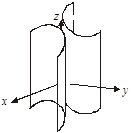
Рис. 3.61

4. — еліптичний параболоїд
(рис. 3.62).

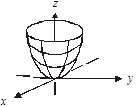
Рис. 3.62

5. 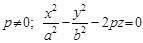. Гіперболічний параболоїд (рис. 3.63).

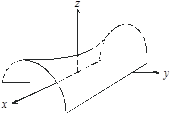
Рис. 3.63

3.6.4. Поверхні у випадку ІІІ

Наведемо приклади поверхонь, що визначаються рівнянням виду (7).

1. 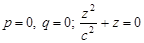— дві паралельні або такі, що збігаю-

ться (r = 0) площини (рис. 3.64)

Рис. 3.64

2. 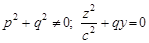— параболічний циліндр (рис. 3.65).

Рис. 3.65

Дата добавления: 2014-11-20