Критерий устойчивости Михайлова

Этот критерий устой­чивости, сформулированный в 1938 г. советским ученым А.В. Михайловым, является, по существу, геометрической интерпретацией принципа аргумента и позволяет судить об устой­чивости системы на основании рассмотрения некоторой кри­вой, называемой кривой Михайлова.

Пусть дано характеристическое уравнение системы:

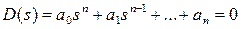(3.87)

Левую часть характеристического уравнения называют ха­рактеристическим полиномом

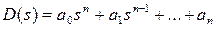(3.88)

Если подставить в этот полином чисто мнимое значение s = jω, то получим комплексный полином

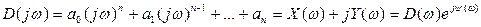(3.89)

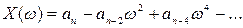, (3.90)

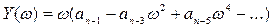(3.91)

называют соответственно вещественной и мнимой функциями Михайлова; функции D(ω) и ψ(ω) представляют собой мо­дуль и фазу (аргумент) вектора .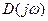

При изменении частоты ω вектор 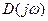, изменяясь по ве­личине и направлению, будет описывать своим концом в ком­плексной плоскости некоторую кривую, называемую кривой (годографом) Михайлова.

В соответствии с (3.85) угол поворота вектора 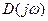вок­руг начала координат при изменении частоты ω от 0 до ∞ ра­вен:

|ω = ∞

Δ Arg D(jω) = (π/2)(n-2m) (3.92)

|ω = 0

Отсюда определяем число правых корней полинома D(s), т. е.

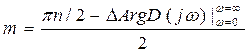(3.93)

Из (3.93) видно, что число правых корней mбудет равно нулю при одном-единственном условии

|ω = ∞

Δ Arg D(jω) = π n/2 (3.94)

|ω = 0

Условие (3.94) является необходимым, но не достаточным условием устойчивости. Для устойчивости системы необходи­мо и достаточно, чтобы все nкорней характеристического уравнения были левыми; иначе говоря, среди них не должно быть корней, лежащих на мнимой оси и обращающих в нуль комп­лексный полином 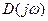, т. е. должно выполняться еще одно условие

D(jω) ≠ 0 (3.95)

Формулы (3.94) и (3.95) представляют математическое выра­жение критерия устойчивости Михайлова. Для того чтобы си­стема автоматического управления была устойчива, необхо­димо и достаточно, чтобы вектор кривой Михайлова 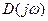при изменении ω от 0 до ∞ повернулся, нигде не обращаясь в нуль, вокруг начала координат против часовой стрелки на угол πn/2, где n — порядок характеристического уравнения.

Заметим, что для устойчивых систем кривая Михайлова на­чинается при ω = 0 на вещественной положительной полуоси, поскольку при а₀ > 0 все коэффициенты характеристического уравнения положительны и D(0)= а_n >0. Кроме того, для устойчивых систем, описываемых обыкновенными дифферен­циальными уравнениями с постоянными коэффициентами, фа­за (аргумент) -ψ(ω) с ростом частоты ω должна возрастать мо­нотонно, т. е вектор 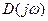должен поворачиваться только против часовой стрелки, поскольку с ростом частоты монотонно возрастают имеющие одинаковые (положительные) знаки, фазы элементарных векторов 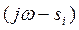, являющиеся слагаемы­ми фазы вектора 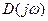(3).

Учитывая сказанное выше, критерий устойчивости Михай­лова можно сформулировать так: для того чтобы система ав­томатического управления была устойчива, необходимо и до­статочно, чтобы кривая (годограф) Михайлова при изменении частоты ω от 0 до ∞, начинаясь при ω = 0 на вещественной положительной полуоси, обходила только против часовой стрелки последовательно n квадрантов координатной плос­кости, где n — порядок характеристического уравнения.

Кривая Михайлова для устойчивых систем всегда имеет плавную спиралевидную форму, причем конец ее уходит в бесконечность в том квадранте координатной плоскости, но­мер которого равен степени характеристического уравнения.

На рис. 3.9 показаны типичные кривые Михайлова для устойчивых систем, описываемых уравнениями, начиная от первого (n= 1) и кончая пятым (n= 5) порядком. Для удоб­ства сравнения коэффициенты а_nво всех случаях приняты оди­наковыми.

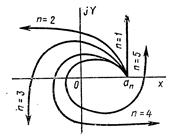
Рис. 3.9. Типичные кривые Михайлова для устойчивых систем

Признаком неустойчивости системы является нарушение числа и последовательности пройденных кривой Михайлова квадрантов координатной плоскости, вследствие чего угол по­ворота вектора 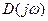оказывается меньше, чем πn/2.Число правых корней неустойчивой системы можно определить по (3.93).

На рис. 3.10 показаны кривые Михайлова для неустойчи­вых систем.

Рис. 3.10, а— при ω = 0 кривая Михайлова начинается на отрицательной вещественной полу­оси; система неустойчива.

Рис. 3.10 б — порядок уравнения n =5, а кривая Михайлова находится вся в одном квадран­те (этому соответствует характеристическое уравнение ); система неустойчива.

Рис. 3.10 в— нарушена последовательность прохождения квадрантов; сис­тема неустойчива.

Рис. 3.10 г—кривая Михайлова начинает­ся в начале координат, т. е. в характеристическом уравне­нии имеется по крайней мере один нулевой корень; система находится на границе апериодической устойчивости; неболь­шая деформация кривой Михайлова (прерывистая линия) де­лает систему устойчивой.

Рис. 3.10 д— кривая Михайлова проходит при некотором значении частоты через начало координат, т. е. в характеристическом уравнении имеются чисто мнимые корни ; система находится на границе ко­лебательной устойчивости; небольшая деформация кривой Михайлова делает систему устойчивой (прерывистая линия).

Рис. 3.10 е— кривая Михайлова проходит через начало ко­ординат, но небольшой деформацией кривой Михайлова удов­летворить условиям устойчивости нельзя; система неустойчи­ва.

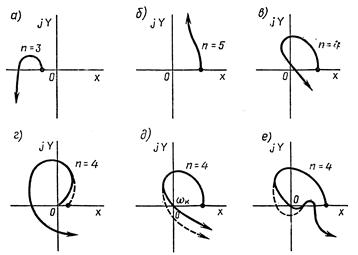
Рис. 3.10. Кривые Михайлова для неустойчи­вых систем.

Для границы устойчивости третьего типа (бесконечный корень)

конец кривой Михайлова перебрасывается как на рис. 3.11. При этом коэффициент 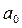будет проходить через нуль, меняя знак плюс на минус.

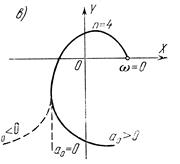
Рис. 3.11. Переход кривой Михайлова

Построение кривой Михайлова практически производится либо методом контрольных точек, либо методом вспомогатель­ных годографов. Первый метод сводится к определению ряда то­чек кривой Михайлова, соответ­ствующих фиксированным значе­ниям частоты ω, включая (обяза­тельно) частоты точек пересечения кривой с осями координат, кото­рые находятся как корни уравне­ний:

X(ω) = 0 (3.96)

Y(ω) = 0 (3.97)

При втором методе предварительно определяют годографы отдельных звеньев си­стемы и по ним строят искомую кривую Михайлова, применяя правила умножения и сложе­ния векторов.

Анализируя годографы Михайлова, можно установить cледующее следствие из критерия устойчивости Михайлова. При последовательном прохождении кривой Михайлова квадран­тов координатной плоскости вещественная и мнимая оси пере­секаются ею поочередно. В точках пересечения кривой Ми­хайлова с вещественной осью обращается в нуль мнимая функ­ция Михайлова Y(ω), а в точках пересечения кривой с мни­мой осью обращается в нуль вещественная функция X(ω). Поэтому значения частот, при которых происходит пересече­ние кривой с вещественной или мнимой осью, должны являть­ся корнями уравнений (3.96) и (3.97)

Вещественную X(ω) и мнимую Y(ω) функции Михайлова можно представить графически в виде кривых (рис. 3.12). Точки пересечения этих кривых с осью абсцисс дают значения корней уравнений (3.96) и (3.97). Если значения 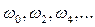есть корни уравнения (3.97), а 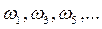- урав­нения (3.96), причем 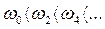, ,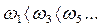то для устойчивой системы обязательно соблюдение нера­венства

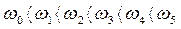… (3.98)

В связи с указанным следствием можно привести другую формулировку критерия устойчивости Михайлова: система автоматического управления будет устойчива тогда и только тогда, когда вещественная X(ω) и мнимая Y(ω) функции Михайлова, приравненные нулю, имеют все действительные и перемежающиеся корни. Общее число этих корней рав­но порядку характеристического уравнения n, и при ω = 0 удовлетворяются условия

X(0) > 0, Y(ω) > 0 (3.99)

На рис. 3.12 а приведен пример графиков X(ω) и Y(ω) для устойчивой системы, а на рис3.12 б — для неустойчивой системы.

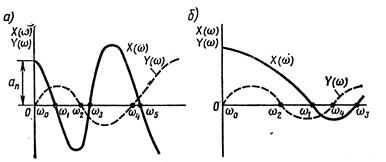
Рис. 3.12. Графики функций X(ω) и Y(ω).

Для уравнений до шестого порядка включительно условие перемежаемости корней дает возможность легко провести ана­литическое исследование устойчивости, не вычерчивая кривую Михайлова. При этом обычно определяют только корни урав­нения Y(ω) = 0. Перемежаемость корней уравнений X(ω)=0 и Y(ω) = 0 можно проверить подстановкой в X(ω) найден­ных корней уравнения Y(ω) = 0. Как видно из рис. 3.12 а, знаки X(ω) при подстановке возрастающих по абсолютной ве­личине корней должны чередоваться.

Пример. Определить устойчивость системы, характеристическое уравнение которой

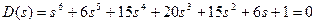(3.100)

Подставляем s = jω и находим вещественную и мнимую функции Ми­хайлова:

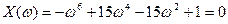(3.101)

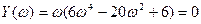(3.102)

Находим корни уравнения Y(ω)=0:

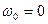
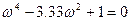(3.103)

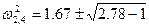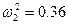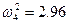, , . (3.104)

Если перемежаются корни, то перемножаются и их квадраты, по­этому нахождение ω₂ и ω₄ не обязательно.

Проверим, чередуются ли знаки X(ω) при подстановке 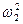и .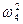

Имеем

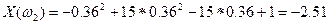(3.105)

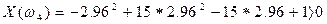(3.106)

Так как все корни Y(ω) вещественны и знаки ординат X(ω),соответствующие этим корням, чередуются, то система устойчива.

Дата добавления: 2014-11-20