Запас устойчивости

Для нормального функционирования всякая САР должна быть достаточно

удалена от границы устойчивости и иметь достаточный запас устойчивости. Необходимость этого обусловлена прежде всего

следующими причинами:

а) уравнения элементов САР, как правило, идеализированы, при их составлении не учитывают второстепенные факторы;

б) при линеаризации уравнений погрешности приближения дополнительно увеличиваются;

в) параметры элементов определяют с некоторой погрешностью;

г) параметры однотипных элементов имеют технологический разброс;

д) при эксплуатации параметры элементов изменяются вследствие старения.
Следовательно, устойчивая по расчету САР, в действительности может оказаться неустойчивой. В следящих системах запас устойчивости необходим еще и для хорошего качества регулирования.
О запасе устойчивости можно судить по расположению корней характеристического уравнения системы: чем дальше отстоят они от мнимой оси (в левой полуплоскости), тем больший запас устойчивости. Каждый критерий устойчивости также позволяет определять запас устойчивости. Количественная оценка запаса устойчивости зависит от того, какой критерий устойчивости выбран. В практике инженерных расчетов наиболее широко используют определение запаса устойчивости на основании критерия Найквиста, по удалению АФЧХ разомкнутой системы от критической точки с координатами [-1,j0], что оценивают двумя показателями: запасом устойчивости по фазе γ и запасом устойчивости по модулю (по амплитуде) h.

Запас устойчивости по фазеопределяют как вели­чину угла 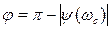для частоты , при ко­торой ; по ам­плитуде— как величину отрезка оси абсцисс h, за­ключенного между крити­ческой точкой (—1, j 0) и ам­плитудно-фазовой характе­ристикой (рис. 3.21).

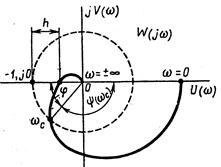
Рис. 3.21. Определение запаса устойчивости по АФЧХ системы

С ростом коэффициента усиления разомкнутой си­стемы модуль амплитудно-фазовой характеристики также растет и при неко­тором значении коэффици­ента усиления , называемого критическим коэффициентом усиления,амплитудно-фазовая харак­теристика пройдет через точку (—1, j0), т. е. си­стема будет на границе ус­тойчивости. При 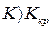система будет неустойчива.

Однако встречаются системы (с внутренними обратными связями), в которых потеря устойчивости может произойти не только при увеличении коэффициента усиления, но также и при его уменьшении. Этим случаям могут соответствовать так называемые клювообразныеамплитудно-фазовые характерис­тики (рис. 3.22). В этих случаях запас устойчивости по амп­литуде определяется величинами двух отрезков hоси абсцисс, заключенных между критической точкой (—1, j0) и амплитуд­но-фазовой характеристикой.

Рис. 3.22. Клювообразнаяамплитудно-фазовая характерис­тика.

Чтобы система обладала требуемым запасом устойчивости при заданных величинах hи φ, около критической точки (—1, j0) вычерчивается некоторая запретная область в виде секто­ра, ограниченного величинами ± hи ±φ, в которую амплитуд­но-фазовая характеристика W(jω) не должна входить (рис. 3.22).

Для устойчивой системы запасы устойчивости γ и h определяют так, как показано на рис. 3.23.

Рис. 3.23. Определение величин γ и h.

Запас по фазе: , где -частота среза, при которой L=0;
Необходнмые значения запасов устойчивости зависят от класса САР и требований к качеству регулирования. Ориентировочно должно быть: γ = 30÷60° и h = 6÷20дб.

Пример 1. Исследовать на устойчивость одноконтурную САР с единичной

обратной связью. Передаточная функция прямой цепи регулятора:

(3.120)

где k_p = 5; τ = 0,08с; Т₁ = 0,1с; Т₂ = 0,05с.

Корни характеристического полинома прямой цепи регуля­тора отрицательные: —10 и —20. Разомкнутая система устойчива и ее АФЧХ (рис. 3.24) не охватывает критической точки с координатами [ — 1, j0]. Поэтому можно заключить, что в замкнутом состоянии рассматриваемая система будет устойчивой.

Рис. 3.24. АФЧХ разомкнутой системы.

Пример 2. Исследовать на устойчивость САР, разомкнутая цепь которой

описывается передаточной функцией:

(3.121)

Прежде всего можно заключить, что характеристический полином имеет чисто мнимые корни, т. е. разомкнутая система на границе устойчивости.

Затем определим частотную передаточную функцию разомкнутой системы:

(3.122)

АФЧХ разомкнутой системы приведена на рис. 3.25.

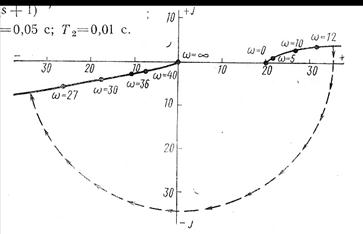
Рис. 3.25. АФЧХ разомкнутой цепи системы, находящейся на колебательной границе устойчивости

При ω = 20с^-1 она имеет разрыв. Если эту кривую дополнить дугой бесконечно большого радиуса, то критическая точка будет находиться вне получившегося контура. Следова­тельно, замкнутая система будет устойчивой.

Пример 3. Выяснить устойчивость САР, у которой передаточная функция разомкнутого контура

(3.123)

где k = 40; τ = 0,25 с; Т₁ = 0,5с; Т₂ = 0,02 с; ξ = 0,1.

Характеристический полином разомкнутой системы имеет один нулевой ко­рень и один положительный вещественный корень s₁ = 2.

Составим частотную передаточную функцию разомкнутой системы:

(3.124)

Теперь определен характер АФЧХ разомкнутой системы (рис. 3.26).

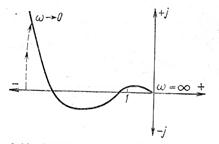
Рис. 3.26. АФЧХ рассматриваемой САР

При ω = 0 АФЧХ имеет разрыв, и поэтому ее нужно дополнить дугой бесконечно большого радиуса от отрицательной вещественной полуоси.

На участке от -1 до - ∞ имеется один положительный переход и полтора отрицательных. Разность между положительными и отрицательными переходами равна - 1/2. Для устойчивости замкнутой системы необходимо, чтобы эта разность равнялась +1/2, так как характеристический полином разомкнутой системы имеет один положительный корень. Следовательно, рассматриваемая система в замкнутом состоянии будет неустойчивой.

Дата добавления: 2014-11-20