
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры выполнения заданий. 1.Докажите: x & Ú º ;
|
|
|
|
1.Докажите: x &  Ú
Ú  º
º  ;
;
1) x &  Ú
Ú  º x &
º x &  Ú &
Ú &  (по закону де Моргана);
(по закону де Моргана);
2) x &  Ú
Ú 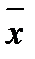 &
&  º
º  & (x Ú
& (x Ú 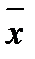 ) (по дистрибутивному закону);
) (по дистрибутивному закону);
3)  & (x Ú
& (x Ú 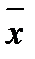 ) º
) º  & И (по закону исключения третьего);
& И (по закону исключения третьего);
4)  & И º
& И º  (по свойству логической константы И).
(по свойству логической константы И).
2. Упростите: x & (y → x) → 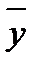 º
º
1) x & (y → x) →  º x & (
º x & (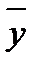 Ú x) →
Ú x) →  (по равносильности);
(по равносильности);
2) x & (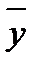 Ú x) →
Ú x) →  º
º  Ú
Ú  (по равносильности);
(по равносильности);
3)  Ú
Ú  º
º 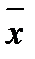 Ú (
Ú ( &
& 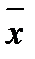 ) Ú
) Ú  (по закону де Моргана);
(по закону де Моргана);
4) 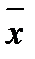 Ú (
Ú ( &
& 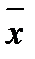 )Ú
)Ú  º
º 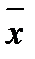 Ú (y&
Ú (y& 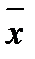 )Ú
)Ú  (по закону снятия дв.отрицания);
(по закону снятия дв.отрицания);
5) 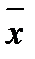 Ú (y &
Ú (y & 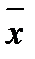 ) Ú
) Ú  º
º 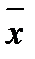 Ú
Ú  (по закону поглощения).
(по закону поглощения).
3.Определите тождественную истинность или ложность формулы
X & Y &  →Y º
→Y º
1) X & Y &  →Y º
→Y º 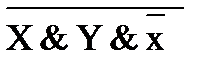 Ú Y (по равносильности)
Ú Y (по равносильности)
2) 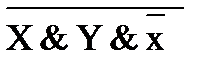 Ú Y º
Ú Y º  Ú
Ú  Ú
Ú  Ú Y (по закону де Моргана)
Ú Y (по закону де Моргана)
3)  Ú
Ú  Ú
Ú 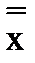 Ú Y º
Ú Y º  Ú
Ú  Ú X Ú Y (по закону снятия дв.отрицания);
Ú X Ú Y (по закону снятия дв.отрицания);
4)  Ú
Ú  Ú X Ú Y º
Ú X Ú Y º  Ú XÚ
Ú XÚ  Ú Y (по коммутативному закону);
Ú Y (по коммутативному закону);
5)  Ú XÚ
Ú XÚ  Ú Y º И Ú И º И (по закону исключения третьего).
Ú Y º И Ú И º И (по закону исключения третьего).
Задания для самостоятельного выполнения
1. Переформулируйте высказывания, если необходимо. Разбейте составные высказывания на простые и запишите их с помощью логической символики. Постройте таблицу истинности.
0) Если усложнить схему устройства, то возрастает его производительность, а если использовать новую элементную базу, то увеличится период эксплуатации. Устройство начнут хорошо раскупать только при одновременном росте его производительности и периода эксплуатации. Но устройство не пользуется спросом.
1) Увеличение денег в обращении влечёт за собой инфляцию. Но рост денежной массы происходит по двум причинам: из-за денежной эмиссии или снижения товарооборота. Снижение товарооборота приводит к безработице и спаду производства. Из-за инфляции падает курс денежной единицы. Рекомендации экономиста Иванова: увеличить денежную эмиссию и поднять производство, тогда избежим безработицы, и курс денежной единицы останется неизменным.
2) Любой марксист-диалектик, но не всякий диалектик-марксист. Любой марксист-материалист, но не всякий материалист-марксист. Гегель был диалектик, но не материалист. Фейербах был материалист, но не диалектик. Итак, если бы Гегель и Фейербах могли объединиться в один кружок, то Маркс уже не понадобился бы.
3) Существуют две теории возникновения человека на земле - теория эволюции Дарвина и теория сотворения человека Господом Богом. Если справедлива теория эволюции, то самопроизвольное возникновение человека без соответствующих превращений живых организмов невозможно. Как доказали учёные, такие превращения действительно имели место. По теории же сотворения человек был слеплен из простой глины, а жизнь в него вдохнул господь. Глины всегда было много, а на счёт дыхания Бога тоже сомневаться не приходиться, поскольку есть на то свидетельство Библии. Отсюда вывод – две названные теории друг другу не противоречат.
4) Из утверждения ”два плюс два равно пяти” следует, что я и папа римский - одно и то же лицо. В самом деле, если от обеих частей указанного равенства отнять по двойке, то будет справедливо равенство ”два равно трём”. Если от обеих частей нового равенства отнять по единице, то будет справедливо равенство - “один равен двум”. Один - это я, а двойка - это я и папа римский. Поскольку верно, что ”один равен двум”, то я есть папа римский.
5) Сегодня посмотрю футбол, если трамвай не задержится. Трамвай не опоздал, но случилась другая беда: у меня не оказалось денег на билет. Рискну доехать «зайцем». В салоне оказался контролер, и я лихорадочно стал рыться по карманам. К моему счастью, нашелся один неиспользованный трамвайный талон. До компостера я добрался вовремя, хотя футбольный матч я так и не увидел: вместе с деньгами я дома оставил и билет на матч.
6) Если в оном месте что-то убудет, то в другом месте что-то прибудет – это истина, не требующая доказательства. Но есть такая теория, которая утверждает: где-то в далеком космосе существуют «черные дыры», куда все проваливается, но оттуда ничего не появляется. Эта теория ничего не говорит о существовании «белых дыр», которые действовали бы противоположно «черным». Один иностранный астрономический журнал сообщил координаты «черной дыры». Российский астроном Иванов направил туда мощный телескоп и ничего не обнаружил. «Так-так, - сказал Иванов, - но «белую дыру» я все же открою».
7) Если в цепи будет большой перепад напряжения, то сгорит предохранитель, что повлечет за собой необходимость его замены. При целом предохранителе телевизор, конечно, будет работать, но только если он включен в сеть питания. Если телевизор работает нормально, то я увижу сегодняшние «Новости». Итак, я смотрю телевизионные «Новости» при условии отсутствия перепада напряжения и подключения телевизора к сети питания.
8) Уменьшение температуры приводит к снижению давления и уменьшению объема. Увеличение объема приводит к росту скорости потока. Повышение давления приводит к падению уровня, если при этом уменьшать температуру. Снижение скорости приводит к уменьшению давления или росту температуры. Технолог Иванов рассудил так: «Мне надо повысить давление при одновременном снижении скорости потока, поэтому я должен увеличить объем и температуру».
9) «Если знать язык программирования, то можно составить рабочую программу. Рабочую программу можно также получить при условии наличия знакомого программиста. Овладеть языком программирования можно, обучаясь в институте. Если программа работает, то ее написал выпускник такого института. Но программа не работает. Это говорит о том, что желающий получить правильный результат не знает языка программирования и не имеет знакомых программистов».
2. Вычислите значения выражений:
0)  Ú b & a ¯ a ~ Ú b & a ¯ a ~ 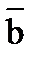
| при а=1, b=0; |
1) а ~ (b |  ) Ú b & ) Ú b & 
| при а=0, b=1; |
2) 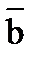 | a Å b → а & b | a Å b → а & b
| при а=0, b=0; |
3) (а | b) Ú 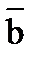 & &  Å а Å а
| при а=0, b=1; |
4)  Ú b | a Ú a ~ Ú b | a Ú a ~ 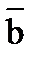
| при а=0, b=1; |
5) а ~ (b →  ) Å b ¯ ) Å b ¯ 
| при а=1, b=0; |
6) 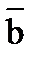 ~ a Å b | а & b ~ a Å b | а & b
| при а=1, b=0; |
7) (а Å b) | 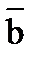 & &  Ú b Ú b
| при а=0, b=0; |
8)  ¯ b & a Ú a ~ ¯ b & a Ú a ~ 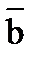
| при а=0, b=0; |
9) а | (b →  ) Å b & ) Å b & 
| при а=0, b=0; |
3. Постройте таблицы истинности формулы алгебры логики:
0)  |b → |b →  & а
1)а → b Å a ¯ с
2)а Ú & а
1)а → b Å a ¯ с
2)а Ú 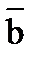 ¯ с → ¯ с →  3)
3)   |с
4)а → |с
4)а →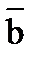 ¯ ¯ 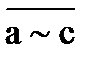
| 5)(a Å b) |  Ú а
6) Ú а
6) 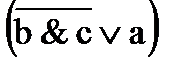 ¯ ¯  7)а ¯ b Ú
7)а ¯ b Ú  & &  8)а & b |
8)а & b | 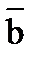 → с
9) → с
9)  → → 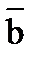 Å с ¯ а Å с ¯ а
| ||||
| a b с | |||||
Практическое занятие №7. Основы алгебры
логики
Задания для самостоятельного выполнения
1. Упростите формулы алгебры логики:
0)X ¯Y & X | 
| 1)X → Y |  & & 
|
2)X Ú Y ¯ 
| 3)X &  → →  | Y | Y
|
4)Y →  Å Y ¯ Å Y ¯ 
| 5)X → YÅ  | | 
|
6)  ¯ ¯  & &  → → 
| 7)  ¯ ¯  & & 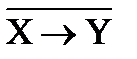
|
8)X Å  Ú Ú  ¯X ¯X
| 9)Y →  ¯ ¯ 
|
2. Определите, какие из формул являются тождественно истинными или тождественно ложными:
0)  & Y ~
& Y ~  →
→  º
º
1)  ~Y & X Ú
~Y & X Ú  ÅY& X º
ÅY& X º
2)  º
º
3) (X ~  ) Ú X Ú Y & (
) Ú X Ú Y & ( Ú
Ú  ) º
) º
4) 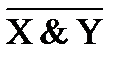 ~
~  Ú
Ú  º
º
5) ((X Ú  ) ® Y) & (
) ® Y) & ( Ú Y) º
Ú Y) º
6) X ® Y ~  ®
®  º
º
7)  & Y ~
& Y ~  ~
~  → X º
→ X º
8)  &
& 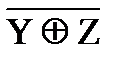 & X º
& X º
9) Y & X ® Y & X & Y º
3. Докажите равносильности, используя законы логики:
0)  Ú (X Ú
Ú (X Ú  ) º X Ú
) º X Ú 
1) (X Ú Y) & (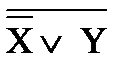 ) & (
) & ( Ú
Ú  ) º Y &
) º Y & 
2) X &  Ú
Ú  & Y & Z Ú X & Z º X &
& Y & Z Ú X & Z º X &  Ú Y & Z
Ú Y & Z
3) (X Ú Y) & (X Ú  ) º X;
) º X;
4) (X & Y Ú Z) & (X Ú Y) Ú Z º X Ú Z Ú Y
5) Y Ú Y &  º Y
º Y
6) 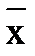 Ú Y & X →
Ú Y & X →  Ú X º X Ú
Ú X º X Ú 
7) Z Ú Y & ZÚ X & 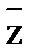 º Z Ú X;
º Z Ú X;
8) Y Ú 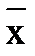 → YÚ X º X Ú Y;
→ YÚ X º X Ú Y;
9) Y &  Ú
Ú  º Y & ZÚ
º Y & ZÚ 
Практическое занятие №8. Логические
функции
| Цель занятия: | 1. | изучить способы представления и суперпозиции логических функций; |
| 2. | привить навыки построения канонических форм логических функций; | |
| 3. | изучить способы определения полноты системы логических функций. |
Логической функцией называют функцию f(x1,x2, … xn) аргументы которой x1,x2, … xn и сама функция принимают значения 0 или 1. Для n = 0 – (нульарные функции) существует 2 различные логические функции, значения: константы И и Л;
n = 1 (унарные функции) существует 4 различных логических функций, значения:
g1(x)=Л; g2(x)=x, g3(x)=x, g4(x)=И,
n = 2 (бинарные функции) существует 16 различных логических функций:
f1(x,y)=0=g1(0) f5(x,y)=Ø(y ® x)
f2(x,y)=x & y f6(x,y)=y=g3(y)
f3(x,y)=Ø(x ® y) f7(x,y)=x Å y
f4(x,y)= x=g3(x) f8(x,y)=x Ú y
f9(x,y)= Ø(x Ú y) f13(x,y)=Øx=g2(x)
f10(x,y)= x ~ y f14(x,y)= x ® y
f11(x,y)=Øy=g2(y) f15(x,y)= Ø(x & y)
f12(x,y)= y ® x f16(x,y)= 1=g4(1)
n = 3 существует 256 различных логических функций и т.д.
Существуют три вида представления логических функций: аналитический (формула), табличный и в виде функциональной схемы и две канонические формы представления: нормальная и совершенная. Классы совершенных форм: совершенная дизъюнктивная нормальная форма (СДНФ), совершенная конъюнктивная нормальная форма (СКНФ) и совершенная полиномиальная нормальная форма (СПНФ).
Механизм построения СДНФ:
1. постройте таблицу истинности логической функции;
2. отметьте наборы переменных, на которых логическая функция истинна;
3. выпишите отмеченные наборы переменных, соединяя между собой операцией конъюнкции, а между наборами – дизъюнкцией. Причем, если переменная имеет ложное значение, то она берется с отрицанием, а если истинное значение, то без отрицания;
4. упростите полученную формулу.
Механизм построения СКНФ:
1. постройте таблицу истинности логической функции;
2. отметьте наборы переменных, на которых логическая функция ложна;
3. выпишите отмеченные наборы переменных, соединяя между собой операцией дизъюнкции, а между наборами – конъюнкцией. Причем, если переменная имеет ложное значение, то она берется без отрицания, а если истинное значение, то с отрицанием;
4. упростите полученную формулу.
Механизм построения СПНФ заключается в замене:
a Ú b= a + b + ab, Øа = 1 + а из СДНФ.
Результат вычисления булевой функции может быть использован в качестве одного из аргументов другой функции. Итог такой операции - суперпозиции можно рассматривать как новую булеву функцию со своей таблицей истинности.
Система булевых функций {f1, f2, …,fn} называется полной, если произвольная булева функция может быть выражена через функции f1, f2, …,fn. Полной является система функций {Ø, &, Ú}.
Теорема о полноте. Если даны две системы логических функций F1, F2 и F1 полна, то система F2 полна тогда, когда каждая функция системы F1 представима через функции F2.
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 1382; Нарушение авторских прав?; Мы поможем в написании вашей работы!