
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Применение булевых функций для анализа и синтеза релейно-контактных схем. Упрощение и преобразование релейно-контактных схем
|
|
|
|
В компьютерах и других автоматических устройствах широко применяются электрические схемы, содержащие сотни и тысячи переключательных элементов: реле, выключателей и т.п. Разработка таких схем весьма трудоёмкое дело. Оказалось, что для разработки и упрощения схем с успехом может быть использован аппарат алгебры логики.
Переключательной схемой считают участок электрической цепи, включающий ряд переключателей. Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Переключателю поставим в соответствие логическую переменную х, которая принимает значение И в том и только в том случае, когда переключатель замкнут и схема проводит ток; если же переключатель разомкнут, то значение х будет Л. Будем считать, что переменные х и 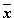 связаны таким образом, что когда контакт х замкнут, то
связаны таким образом, что когда контакт х замкнут, то 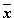 разомкнут, и наоборот.
разомкнут, и наоборот.
Всей переключательной схеме можно поставить в соответствие логическую переменную, равную И, если схема проводит ток, и равную Л - если не проводит. Эта переменная является функцией от переменных, соответствующих всем переключателям схемы, и называется функцией проводимости.
Найдем функции проводимости F некоторых переключательных схем:
a) 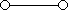 - схема не содержит переключателей и проводит ток всегда, следовательно F = И;
- схема не содержит переключателей и проводит ток всегда, следовательно F = И;
б)  - схема содержит один постоянно разомкнутый контакт, следовательно F = Л;
- схема содержит один постоянно разомкнутый контакт, следовательно F = Л;
в) 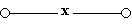 - схема проводит ток, когда переключатель х замкнут, и не проводит, когда х разомкнут, следовательно, F(x) = x;
- схема проводит ток, когда переключатель х замкнут, и не проводит, когда х разомкнут, следовательно, F(x) = x;
г) 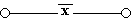 - схема проводит ток, когда переключатель х разомкнут, и не проводит, когда х замкнут, следовательно, F(x) =
- схема проводит ток, когда переключатель х разомкнут, и не проводит, когда х замкнут, следовательно, F(x) = 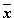 ;
;
д) 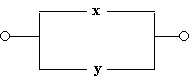 - схема проводит ток, когда хотя бы один из переключателей замкнут (параллельное соединение), следовательно, F(x, y) = x Ú y.
- схема проводит ток, когда хотя бы один из переключателей замкнут (параллельное соединение), следовательно, F(x, y) = x Ú y.
е)  - схема проводит ток, когда оба переключателя замкнуты (последовательное соединение), следовательно, F(x, y) = x & y;
- схема проводит ток, когда оба переключателя замкнуты (последовательное соединение), следовательно, F(x, y) = x & y;
При рассмотрении переключательных схем возникают две основные задачи: синтез и анализ схемы.
Синтез схемы по заданным условиям ее работы сводится к:
- составлению функции проводимости по таблице истинности, отражающей эти условия;
- упрощению этой функции;
- построению соответствующей схемы.
Анализ схемы сводится к:
- определению значений её функции проводимости при всех возможных наборах входящих в эту функцию переменных.
- получению упрощённой формулы.
Примеры выполнения заданий:
1. Необходимо спроектировать (синтезировать) электрическую цепь, содержащую 4 переключателя x, y, z и t, такую, чтобы она проводила ток тогда и только тогда, когда замкнут контакт переключателя t и какой-нибудь из остальных трёх контактов.
Функция имеет вид: F(x, y, z, t) = t & (x Ú y Ú z). Схема имеет вид:

2. Требуется произвести анализ схемы:
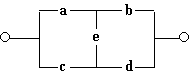
Имеется четыре возможных пути прохождения тока при замкнутых переключателях a, b, c, d, e: через переключатели a, b; через переключатели a, e, d; через переключатели c, d и через переключатели c, e, b. Функция проводимости имеет вид: F(a, b, c, d, e) = a & b Ú a & e & d Ú c & d Ú c & e & b или F(a, b, c, d, e) = a & (b Ú e & d) Ú c & (d Ú e & b).
3. Требуется произвести анализ и, если возможно, упрощение схемы. Постройте упрощенную схему.

Функция проводимости имеет вид: F(x, y, z) = 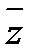 &(
&(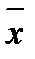 Ú y)Ú (zÚ x&
Ú y)Ú (zÚ x& 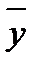 )
)
F(x, y, z) = 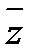 &
& 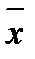 Ú
Ú 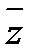 & y Ú z Ú x &
& y Ú z Ú x & 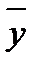 º
º
º 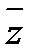 &
& 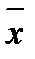 Ú (
Ú (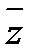 Ú z) & (y Ú z) Ú x &
Ú z) & (y Ú z) Ú x & 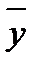 º
º
º 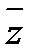 &
& 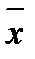 Ú И & (y Ú z) Ú x &
Ú И & (y Ú z) Ú x & 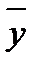 º
º 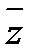 &
& 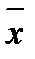 Ú y Ú z Ú x &
Ú y Ú z Ú x & 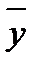 º
º
º 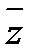 &
& 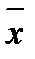 Ú z Ú x &
Ú z Ú x & 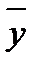 Ú y º (
Ú y º (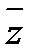 Ú z) & (
Ú z) & (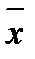 Ú z) Ú (x Ú y) & (
Ú z) Ú (x Ú y) & (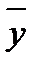 Ú y) º
Ú y) º
º И & (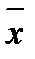 Ú z) Ú (x Ú y) & И º
Ú z) Ú (x Ú y) & И º 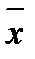 Ú z Ú x Ú y º И Ú y Ú z º И
Ú z Ú x Ú y º И Ú y Ú z º И
Упрощенная схема имеет вид: 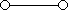
4. Проверьте равносильность следующих переключательных схем:

Функция проводимости имеет вид:
F(a, b, c) = (a Ú 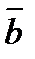 )& c Ú a &
)& c Ú a &  Ú c & (b Ú
Ú c & (b Ú 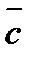 ).
).
F(a, b, c) = a & c Ú 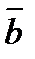 & c Ú a &
& c Ú a &  Ú c & b Ú c &
Ú c & b Ú c & 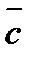 º
º
º a & (c Ú  ) Ú с & (
) Ú с & (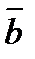 Ú b) Ú Л º a & И Ú с & И º a Ú с
Ú b) Ú Л º a & И Ú с & И º a Ú с
Переключательные схемы равносильны.
Задания для самостоятельного выполнения
1. Минимизируйте методом Квайна - МакКласски булеву функцию
f(x1, x2,x3, x4), заданную таблицей истинности:
| x4x3x2x1 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 |
| 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 | 1 1 0 0 0 1 0 1 0 1 1 0 0 0 0 0 | 0 0 0 1 1 1 0 1 0 0 0 0 1 0 0 1 | 0 1 1 0 0 0 1 0 0 0 1 1 0 0 1 0 | 1 0 0 1 0 1 0 1 0 0 0 0 0 0 1 1 | 0 1 0 1 0 0 0 0 1 1 0 0 1 1 0 0 | 0 0 1 1 0 1 0 1 0 0 1 1 0 0 0 0 | 1 1 0 0 1 0 0 0 0 1 0 0 1 0 0 1 | 0 0 0 1 0 1 0 0 1 0 1 1 0 1 0 0 | 0 1 1 1 0 0 0 1 0 1 1 0 0 0 0 0 | 1 0 0 0 1 1 0 0 0 0 0 1 0 0 1 1 |
Решение:
| Номер группы | Двоичные номера наборов единицы | Номер группы | Двоичные номера наборов единицы |
| Простые импликанты | Наборы единицы | |||||||
МДНФ=
2. Укажите функцию F(x1, x2, x3, x4), реализуемую схемой из функциональных элементов:
0) F(x1, x2, x3, x4) =
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 1937; Нарушение авторских прав?; Мы поможем в написании вашей работы!