Средняя арифметическая и ее свойства

Эмпирические и теоретические частоты.

Асимметрия и эксцесс ряда распределения.

Моменты ряда распределения и связь между ними.

Дисперсия ряда распределения и ее свойства. Среднее квадратическое отклонение.

Средняя арифметическая и ее свойства.

Лекция 2 Вопросы

Вариационные ряды позволяют получить первое представление об изучаемом распределении. Далее необходимо исследовать числовые характеристики распределения: положения (средняя арифметическая, мода, медиана); рассеяния (дисперсия, среднее квадратическое отклонение, коэффициент вариации); меры скошенности (коэффициент асимметрии) и островершинности (эксцесс) распределения.

Средней арифметической (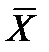) дискретного вариационного ряда называется отношение суммы произведений вариант на соответствующие частоты к объему совокупности:

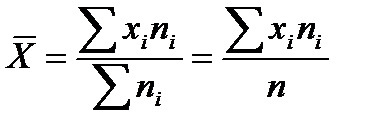. (9.6)

Средняя арифметическая имеет те же единицы измерения, что и варианты.

Свойства средней арифметической.

1. Средняя арифметическая суммы соответствующих друг другу значений, принадлежащих двум группам наблюдений, равна алгебраической сумме средних арифметических этих групп:

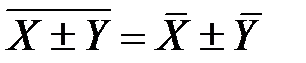. (9.7)

2. Если ряд наблюдений состоит из двух непересекающихся групп наблюдений, то средняя арифметическая 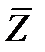всего ряда наблюдений равна взвешенной средней арифметической групповых средних 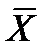и 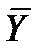, причём весами являются объёмы групп 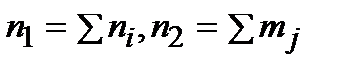соответственно

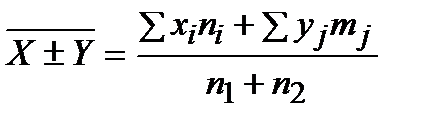. (9.8)

3. Средняя арифметическая постоянной равна самой постоянной

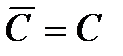
4. Если все варианты умножить на одно и то же число, то средняя арифметическая увеличится в то же число раз:

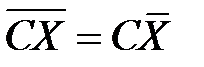. (9.9)

5. Сумма отклонений результатов наблюдений от их средней, взвешенная с соответствующими частотами равна нулю

.

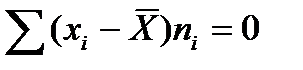6. Если все варианты увеличить (уменьшить) на одно и то же число, то средняя арифметическая увеличится (уменьшится) на то же число, т.е.:

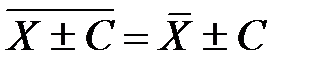. (9.10)

7. Если все частоты вариантов умножить на одно и то же число, то средняя арифметическая не изменится.

Модой 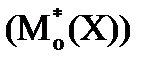дискретного вариационного ряда называется вариант, имеющий наибольшую частоту.

Медианой 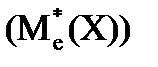дискретного вариационного ряда называется вариант, делящий ряд на две равные части.

Если дискретный вариационный ряд имеет 2n членов в ранжированной совокупности: х_1, х₂,…,х_n, х_n+1,…,x_2n, то

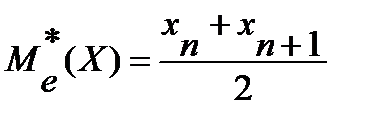. (9.11)

Если дискретный вариационный ряд в ранжированной совокупности имеет 2n+1 членов: х_1, х₂,…,х_n-1, х_n, х_n+1,…,x_2n+1, то

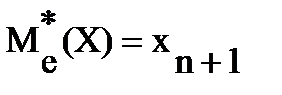. (9.12)

Для интервальных вариационных рядов имеют место формулы:

а) медианы:

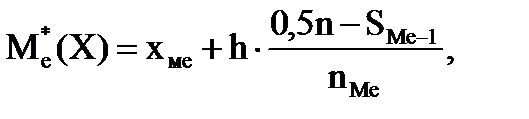(9.13)

где х_Ме – начало медианного интервала,

h – длина частичного интервала,

n – объем совокупности,

S_Ме-1 – накопленная частота интервала, предшествующего медианному,

n_Ме – частота медианного интервала;

б) моды:

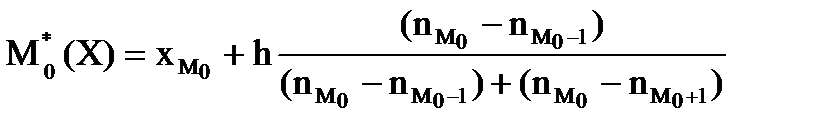, (9.14)

где х_Мо – начало модального интервала,

h – длина частичного интервала,

n_Мо – частота модального интервала,

n_Мо-1 - частота предмодального интервала,

n_Мо+1 - частота послемодального интервала;

в) средней арифметической, совпадающей с формулой (3.2.1) для дискретного вариационного ряда, причем в качестве вариант x_i принимаются середины соответствующих интервалов.

Мода и медиана используются в качестве характеристики среднего

положения в случае, если границы ряда нечеткие или если ряд не симметричен.

Дата добавления: 2014-11-20