Дисперсия ряда распределения и ее свойства. Среднее квадратическое отклонение

Показатели центральной тенденции (М₀,М_е, 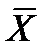) не исчерпывают всех свойств распределения. В одних случаях значения признака концентрируются тесно около среднего значения, в других наблюдается значительное рассеяние.

Для изучения степени изменчивости признака вводят показатели вариации:

– размах вариации W=x_max-x_min. (9.15)

- дисперсия дискретного ряда распределения

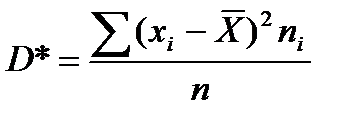(9.16)

характеризует средний квадрат отклонения х_i от .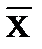

Среднее квадратическое отклонение дискретного ряда распределения:

, (9.17)

выражается в тех же единицах, что и х_i.

Среднее линейное отклонение:

. (9.18)

Коэффициент вариации:

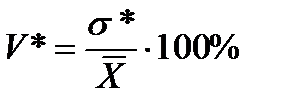, (9.1.9)

характеризует относительное значение среднего квадратического отклонения и обычно служит для сравнения колеблемости несоизмеримых показателей.

Свойства дисперсии:

1.Дисперсия постоянной величины равна 0

D^*(C)=0.

2.Если все результаты наблюдений увеличить (уменьшить) на одно и то же число С, то дисперсия и среднее квадратическое отклонение не изменятся, т.е.

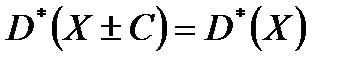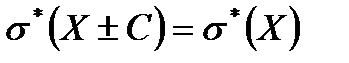, (9.20)

3.Если все результаты наблюдений умножить на одно и то же число, то имеет место равенство:

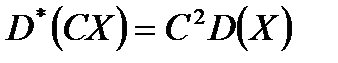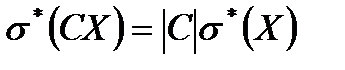, (9.21)

4.Если все частоты вариантов умножить на одно и то же число, то дисперсия и среднее квадратическое отклонение не изменятся.

5.Свойство минимальности дисперсии.

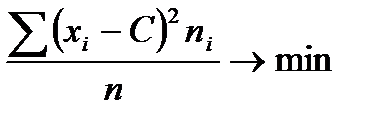при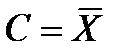

Следствие 1. Средний квадрат отклонений значений x_i от их средней арифметической равен среднему квадрату отклонений x_i от произвольной постоянной а минус квадрат разности между средней арифметической (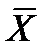) и этой произвольной постоянной.

Пусть 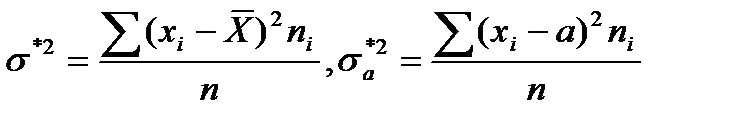, тогда

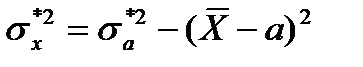. (9.22)

Следствие 2. Дисперсия равна средней арифметической из квадратов значений признака минус квадрат средней арифметической

.

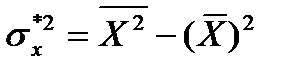6.Правило сложения дисперсий. Если объединяются несколько распределений в одно, то общая дисперсия σ₀^*2 нового распределения равна средней арифметической из дисперсий объединяемых распределений, сложенной с дисперсией частных средних относительно общей средней нового распределения. Или, иначе говоря, общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:

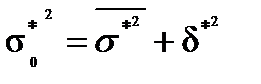(9.23)

или

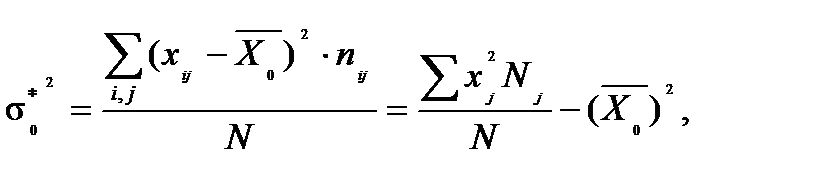
где n_ij – частота j–го варианта i-го частного распределения (j=1,…, m; i=1,2,…, к)

x_ij – j–й вариант i-го частного распределения (j=1,…, m; i=1,2,…, к),

n_i – объем i-го частного распределения,

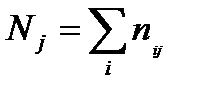– частота j-го варианта нового распределения,

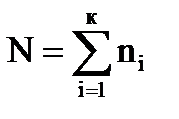- объем нового распределения,

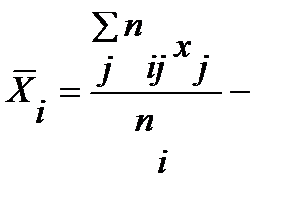средняя арифметическая i-го частного распределения, (i=1,...,к),

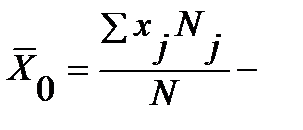средняя арифметическая нового распределения,

дисперсия i-го частного распределения,

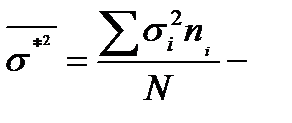внутригрупповая дисперсия,

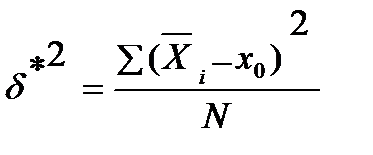- межгрупповая дисперсия.

Дата добавления: 2014-11-20