
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференциальное уравнение движения 1 страница
|
|
|
|
Аналитическое и численное исследование задач связано с применением основных законов течения в дифференциальной форме. Для процессов, происходящих в нефте-газовых пластах, характерно изменение основных параметров течения во времени. Такие процессы называются неустановившимися (нестационарными). Для получения дифференциальных уравнений движения выделяется бесконечно-малый элемент и рассматриваются законы сохранения массы, количества движения и энергии за бесконечно малый промежуток времени. При этом используются экспериментальные соотношения, определяющие зависимость силы трения, пористости и т.д. от параметров течения. Число уравнений должно равняться числу неизвестных параметров, что даёт замкнутую систему.
Для подземной гидромеханики характерно изотермическое изменение параметров вследствие значительных величин удельной поверхности коллекторов и их теплоёмкости. Т.о. для таких процессов можно не рассматривать уравнение энергии и ограничиваться уравнениями балланса массы (неразрывности) и движения.
Уравнение энергии необходимо рассматривать в локальных областях призабойной зоны из-за значительных перепадов давления, проявления дроссельного эффекта, а также при применении тепловых методов повышения нефте-газоотдачи.
Для замыкания системы уравнений необходимо введение замыкающих соотношений, а именно уравнений состояния флюидов и пористой среды. Кроме того для получения однозначного решения необходимо задание граничных и начальных условий.
В большинстве случаев решение задач подземной гидродинамике требует использования численных методов и только в сильно идеализированных случаях одномерного течения удаётся получить аналитическое решение.
Рассмотрим фильтрацию флюидов в пористых средах, принимая во внимание линейный закон Дарси.
Выделим два сечения – первое на расстоянии S от начала отсчета вдоль линии тока, второе – на расстоянии DS от первого (рис. 1).
Движение флюида происходи в направлении возрастания координаты S. В сечении с координатой S обозначим приведенное давление через p*(S, t), в сечении координат S + DS – через p*(S + DS,t), используя формулу 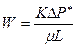 ,
,
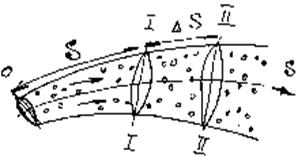 получаем
получаем
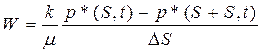 , (20) Рис. 1. Трубка тока
, (20) Рис. 1. Трубка тока
или перейдем к пределу при  ,
,
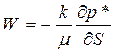 , (21)
, (21)
Знак (-) в правой части означает, что приведенное давление падает по движению жидкости, т.е. градиент приведенного давления отрицателен 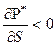 .
.
Формула (21) справедлива только для изотропной среды, для которой характерно постоянство проницаемости по всем направлениям в окрестности рассматриваемой точки. Однако с переходом от точки к точке пласта проницаемость может и изменяться, таким образом 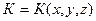 (модель изотропного неоднородного пласта).
(модель изотропного неоднородного пласта).
Запишем уравнение (21) в проекциях на оси координат x, y, z. Если обозначить через 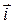 ,
, 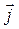 ,
, 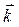 единичные векторы вдоль осей координат, вектор скорости фильтрации можно записать в виде
единичные векторы вдоль осей координат, вектор скорости фильтрации можно записать в виде
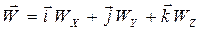 , (22)
, (22)
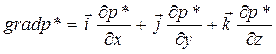 , (23)
, (23)
тогда
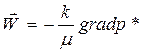 , (24)
, (24)
или в проекциях на оси координат
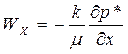 ,
, 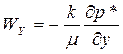 ,
, 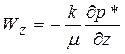 , (25)
, (25)
если ось z направлена вверх 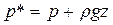 и дифференциальные уравнения движения примут вид
и дифференциальные уравнения движения примут вид
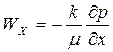 ,
, 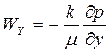 ,
, 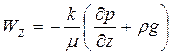 , (26)
, (26)
в векторной форме 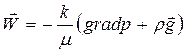 . (27)
. (27)
В дифференциальной форме двучленный закон записывается в виде 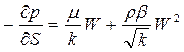 , (28)
, (28)
где S – координата, взятая вдоль линии тока по движению жидкости.
В векторной форме двучленный закон выведен из теории размерностей, в виде
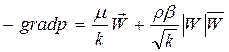 (29)
(29)
В прекциях на оси координат имеем
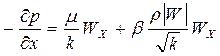 , (30)
, (30)
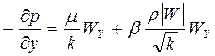 ,
,
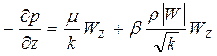 .
.
При фильтрации неньютоновских вязкопластичных жидкостей, а также при фильтрации с очень малыми скоростями имеет место закон фильтрации (5), который отличается от закона Дарси наличием предельного градиента 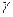 , по достижении которого начинается движение. В векторной форме закон фильтрации с предельным градиентом выведен из теории размерностей и имеет вид
, по достижении которого начинается движение. В векторной форме закон фильтрации с предельным градиентом выведен из теории размерностей и имеет вид 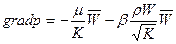 . (31)
. (31)
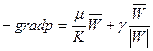 ; (32)
; (32)
в проекции на оси координат:
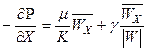 ; (33)
; (33)
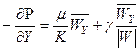 ;
;
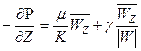 .
.
Лекция 3.
Вывод дифференциального уравнения неустановившейся фильтрации однородного флюида по закону Дарси. Функция Л. С. Лейбензона.
Для вывода дифференциального уравнения неустановившейся фильтрации используем уравнение неразрывности
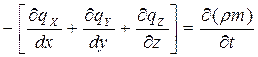
или
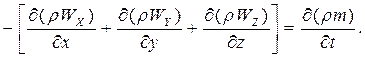 (34)
(34)
Сумма в скобках в левой части уравнения (34) представляет собой дивергенцию вектора скорости фильтрации 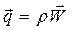 и кратко записывается таким образом:
и кратко записывается таким образом:
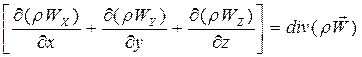 , (35)
, (35)
поэтому уравнение (34) можно записать в виде:
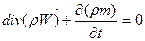 . (36)
. (36)
Уравнение (34) (или 36) справедливо только в том случае, если внутри объема 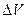 нет источников или стоков, выделяющих или поглощающих флюид, не происходит химических реакций, фазовых превращений и т.д.
нет источников или стоков, выделяющих или поглощающих флюид, не происходит химических реакций, фазовых превращений и т.д.
И уравнения движения
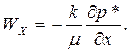
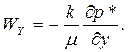
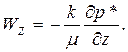 (37)
(37)
В уравнении (11) не будем учитывать силу тяжести.
Введем функцию 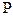 (функцию Лейбензона), тогда дифференциал этой функции равен:
(функцию Лейбензона), тогда дифференциал этой функции равен:
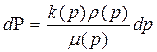 , (38)
, (38)
тогда
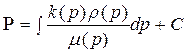 , (39)
, (39)
т. к. функция Лейбензона и давление зависит от координат x, y, z и времени t, то (38) можно записать в развернутом виде, используя понятие полного дифференциала функции от многих переменных:
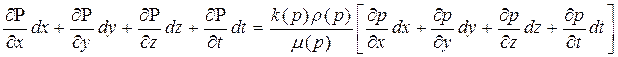 .
.
Сравнивая коэффициенты при x, y, z получаем:
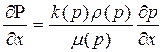 ,
, 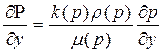 ,
, 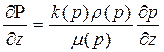 , (40)
, (40)
Запишем выражение для составляющих массовой скорости фильтрации, умножив правую и левую части уравнения (37) на плотность и используя соотношения (40):
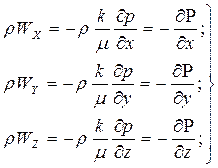 , (41)
, (41)
Подставим выражение (41) в уравнение неразрывности (34), получим:
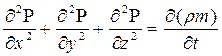 (42)
(42)
или
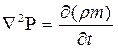 , (43)
, (43)
где 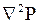 - оператор Лапласа от функции Лейбензона (39).
- оператор Лапласа от функции Лейбензона (39).
Уравнение (42) справедливо для неустановившегося движения однородного флюида в однородной пористой среде по закону Дарси.
При установившейся фильтрации 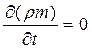 и будет удовлетворяться уравнение Лапласа для функции Лейбензона:
и будет удовлетворяться уравнение Лапласа для функции Лейбензона:
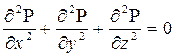 (44)
(44)
При k = const, m = const, и 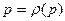 , тогда можно ввести функцию Лейбензона в виде:
, тогда можно ввести функцию Лейбензона в виде:
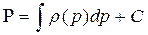 . (45)
. (45)
Тогда дифференциальное уравнение неустановившейся фильтрации примет вид:
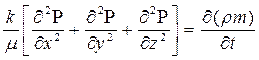 . (46)
. (46)
Выразим функцию Лейбензона (45) через давление для различных флюидов – несжимаемой жидкости, упругой жидкости, совершенного газа и реального газа. Для этого в (45) подставим соответствующие выражения для плотности и проинтегрируем.
Для несжимаемой жидкости r о = const, тогда
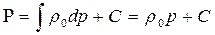 , (47)
, (47)
т. е. функция Лейбензона пропорциональна давлению.
Для упругой жидкости:
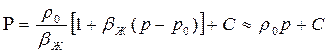 , (48)
, (48)
т. е. имеем тот же вид, что и для несжимаемой жидкости.
Для совершенного газа с уравнением состояния
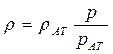 , (49)
, (49)
получаем
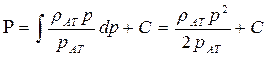 , (50)
, (50)
т. е. функция Лейбензона пропорциональна квадрату давления.
Для реального газа с уравнением состояния
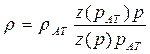 , (51)
, (51)
тогда
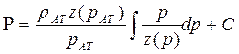 , (52)
, (52)
т. е. функция Лейбензона записывается в виде интеграла.
Т. к. реальные свойства газа проявляются при высоких пластовых давлениях, то в этом случае оказывается существенной зависимость вязкости от давления и нужно использовать функцию Лейбензона в виде (39).
Лекция 4.
1. Установившиеся потоки флюида в пористой среде.
Одномерным называется фильтрационный поток жидкости или газа, в котором скорость фильтрации, давление и другие характеристики течения являются функциями только одной координаты, отсчитываемой вдоль линии тока.
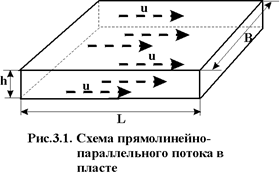
1.Прямолинейно-параллельный поток.Траектории всех частиц жидкости - параллельные прямые, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока равны между собой, поверхности равных потенциалов (эквипотенциальные поверхности) и поверхности равных скоростей (изотахи) являются плоскими поверхностями перпендикулярными траекториям. Законы движения вдоль всех траекторий такого фильтрационного потока идентичны, а потому достаточно изучить движение вдоль одной из траекторий, которую можно принять за ось координат - ось х.
Примеры.
|
а) Пласт (рис.3.1) имеет в плане полосообразную форму шириной B и длиной L, толщина пласта h постоянна, граничный контур непроницаем и непроницаемы кровля и подошва пласта. Батарея эксплуатационных скважин расположена параллельно начальному контуру нефтеносности. Приближение тем больше, чем меньше расстояние между скважинами и если заменить батарею сплошной прямолинейной выработкой - галереей, то движение жидкости к галерее будет строго прямолинейно-параллельным.
б) Поток между круговыми батареями нагнетательных и эксплуатационных скважин в случае больших радиусов батарей (угол схождения векторов скорости бесконечно мал). При этом толщина пласта постоянна, а его кровля и подошва непроницаемы.
в) в лабораторных условиях при течении через цилиндрический керн или прямую трубу постоянного сечения, заполненную пористой средой.
2. Плоскорадиальный поток.Траектории всех частиц жидкости - прямолинейные горизонтальные прямые, радиально сходящиеся к центру скважины, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока параллельны и равны между собой; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют цилиндрические окружности с осью, совпадающей с осью скважины. Схемы линий тока в любой горизонтальной плоскости потока будут идентичными и для характеристики потока достаточно рассмотреть движение жидкости в одной горизонтальной плоскости.
Примеры.
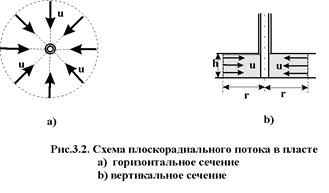
а) Горизонтальный пласт постоянной толщины (h) и неограниченной протяженности, подошва и кровля пласта непроницаемы. Пласт вскрыт единственной гидродинамически совершенной скважиной (рис. 3.2), т.е. вскрыт на всю толщину и забой полностью открыт. Для эксплуатационной скважины поток - радиально-сходящий, а для нагнетательной - радиально-расходящий. Плоско-радиальным потоком будет занята вся зона от стенки скважины до контура питания.
б) Гидродинамически- несовершенная скважина - вблизи скважины линии тока искривляются и поток можно считать плоско-радиальным только при некотором удалении от скважины.
в) Круговая батарея эксплуатационных скважин - поток плоско-радиален на некотором удалении, т.к. жидкость движется как бы к укрупнённой скважине радиуса, равного радиусу окружности батареи.
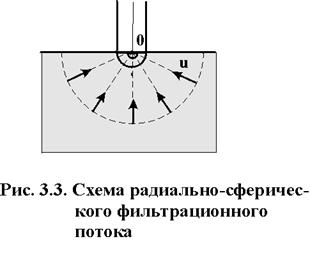
3. Радиально-сферический поток. Траектории всех частиц жидкости - прямолинейные горизонтальные прямые, радиально сходящиеся к центру полусферического забоя; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют сферические поверхности. Скорость фильтрации в любой точке потока является функцией только расстояния этой точки от центра забоя. Следовательно, этот вид фильтрационного потока также является одномерным.
|
Такой поток может реализовываться, когда скважина вскрывает только плоскую горизонтальную, непроницаемую кровлю пласта (рис.3.3). Пласт при этом должен быть неограниченной толщины, а забой иметь полусферическую форму. Приближение к данному виду потока тем лучше, чем глубина вскрытия меньше толщины пласта.
Описанные три вида одномерного потока играют большую роль при решении многих задач нефте-газопромысловой практики. Они лежат в основе ряда исследований закономерностей течения жидкости в пласте в зависимости от принятой системы разработки или от конструктивных особенностей скважин. Естественно, моделируя каждый из трёх видов одномерного потока, мы прибегаем к некоторой схематизации реальных пластов и течений жидкости. Тем не менее рассмотренные схемы не только воспроизводят хотя и приближенно простейшие случаи течения жидкости в реальном пласте, но и помогают изучать более сложные виды потоков пластовой жидкости в тех случаях, в которых сложный фильтрационный поток удобно представить себе состоящим из простейших видов потока.
К числу сложных потоков можно отнести: плоский фильтрационный поток в случае, когда число скважин не менее двух; многофазные течения и т.д.
Задача исследования установившегося фильтрационного потока заключается в определении дебита (расхода), давления, градиента давления и скорости фильтрации в любой точке потока, а также в установлении закона движения частиц жидкости (или газа) вдоль их траекторий и в определении средневзвешенного по объёму порового пространства пластового давления.
При условии вытеснения флюида из пласта или его нагнетания в пласт через галерею или скважину условимся принимать за координату произвольной точки пласта расстояние r до этой точки от:
1) галереи (для прямолинейно- параллельного потока);
2) центра контура скважины в основной плоскости (плоскости подошвы пласта) фильтрации (для плоско-радиального потока);
3) центра полусферического забоя скважины (для сферически-радиального потока).
2.Характеристики одномерных фильтрационных потоков
жидкости и газов.
Для расчета перечисленных характеристик одномерных фильтрационных потоков жидкости и газа можно использовать два подхода. Первый из них – вывод дифференциальных уравнений и их решение отдельно для прямолинейно-параллельного, плоскорадиального и радиально-сферического потоков жидкости и газа. Второй – вывод обобщенного уравнения одномерного течения флюида в недеформируемой трубке тока переменного сечения с использованием функции Лейбензона и получение из него конкретных формул применительно к различным схемам фильтрационных потоков. Второй подход более эффективен, позволяет исходить из обобщенных характеристик течения, он был использован и при выводе следующих характеристик:
Прямолинейно – параллельный фильтрационный поток.
Площадь поперечного сечения 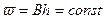 ; на контуре питания x1=0, P1=PK, на галерее x2=L, P2=PГ;
; на контуре питания x1=0, P1=PK, на галерее x2=L, P2=PГ;
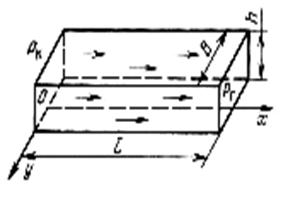 |
Схема прямолинейно параллельного течения в пласте
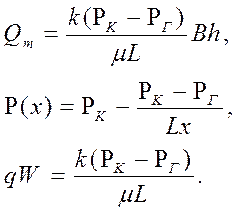 (53, 54, 55)
(53, 54, 55)
Плоскорадиальный фильтрационный поток
От координаты S переходим к r, отсчитываемой от центра скважины. Для добывающей скважины 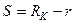 ,
, 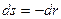 , площадь фильтрционной поверхности
, площадь фильтрционной поверхности 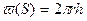 - боковая поверхность цилиндра; на контуре питания r 1 = R k,P2=PK на забое скважины r 2 = r c,P2=PC.
- боковая поверхность цилиндра; на контуре питания r 1 = R k,P2=PK на забое скважины r 2 = r c,P2=PC.
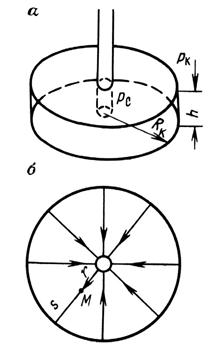 |
Схема плоско – радиального потока в круговом пласте.
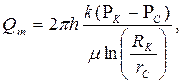 (56)
(56)
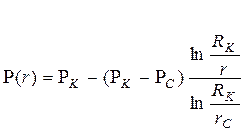 , (57)
, (57)
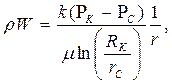 (58)
(58)
Радиально – сферический фильтрационный поток.
В этом случае для добывающей скважины с полусферическим забоем имеем: 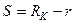 ,
, 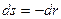 ,
, 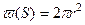 - площадь поверхности полусферы с радиусом r, r 1 = R k, P1=PK, r 2= r C, P2=PC.
- площадь поверхности полусферы с радиусом r, r 1 = R k, P1=PK, r 2= r C, P2=PC.
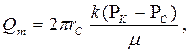 (59)
(59)
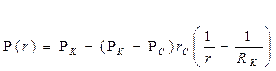 ; (60)
; (60)
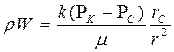 . (61)
. (61)
3. Анализ одномерных потоков несжимаемой жидкости и газа.
Рассмотрим конкретные модели флюидов – несжимаемую жидкость и совершенный газ. Выпишем для них формулы для расчета основных характеристик одномерных фильтрационных потоков. Сопоставление этих формул позволит оценить эффект сжимаемости при прочих одинаковых условиях.
Прямолинейно – параллельный поток несжимаемой жидкости и совершенного газа
Подставим в основные расчетные формулы (53), (54), (55) выражение функции Лейбензона (для несжимаемой жидкости) 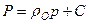 и (для совершенного газа)
и (для совершенного газа) 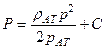 , а также на контуре
, а также на контуре 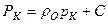 и на галерее
и на галерее 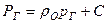 (аналогично и для совершенного газа)
(аналогично и для совершенного газа)
Расчетные формулы для прямолинейно-параллельного потока несжимаемой жидкости и совершенного газа
| Характеристика | Несжимаемая жидкость | Совершенный газ |
| Функция Лейбензона | 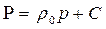
| 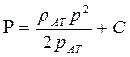
|
| Распределение давления по пласту, 0 £ x £ L | 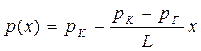 (62) (62)
| 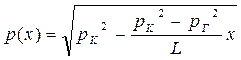 (63)
(63)
|
| Массовый расход Qm | 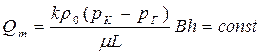 (64)
(64)
| 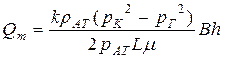 (65)
(65)
|
| Массовая скорость фильтрации | 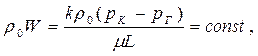 (66)
(66)
| 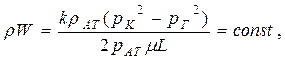 (67)
(67)
|
| Объемный расход Q | 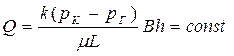 (68) (68)
| 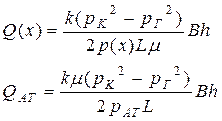
|
| Скорость Фильтрации (объемная) | 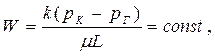 (71)
(71)
| 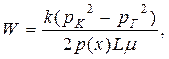 (72)
(72)
|
| Средневзвешенное давление | 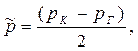 (73)
(73)
| 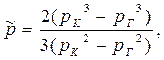 (74)
(74)
|
| Время движения отмеченных частиц t | 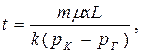 (75)
(75)
| 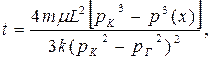 (76)
(76)
|
| Время продви – жения до галереи Т | 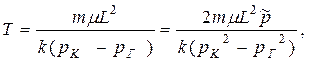 (77) (77)
| 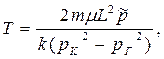 (78)
(78)
|
Массовые расходы и массовые скорости фильтрации для обоих флюидов постоянны вдоль пласта; объемный расход и объемная скорость фильтрации жидкости вдоль пласта не меняются, однако для газа эти характеристики зависят от координаты, возрастая от входа к выходу, что является следствием расширения газа при снижении давления.
Плоскорадиальный фильтрационный поток
Модель флюида
| Характеристика | Несжимаемая жидкость | Совершенный газ |
| Распределение давления по пласту | 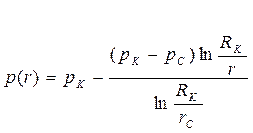 (79)
(79)
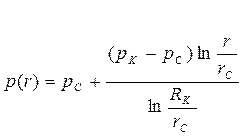 (81)
(81)
| 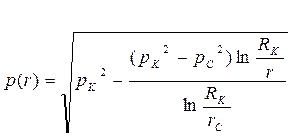 (80)
(80)
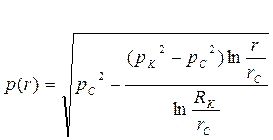 (82)
(82)
|
| Массовый расход Q m | 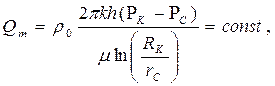 (83) (83)
| 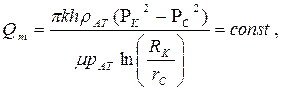 (84)
(84)
|
| Массовая скорость фильтрации rW | 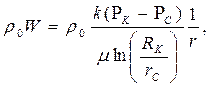 (85)
(85)
| 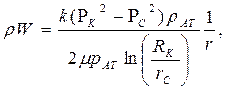 (86)
(86)
|
| Объемный расход Q | 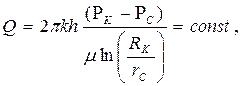 (формула Дюпюи) (87)
(формула Дюпюи) (87)
| 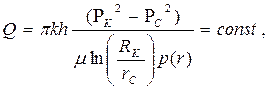 (88)
(88) 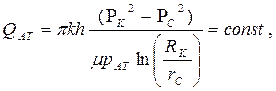 (89)
(89)
|
| Объемная скорость фильтрации |  (90)
(90)
| 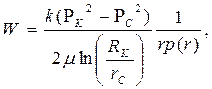 (91)
(91)
|
| Средневзвешенное давление | 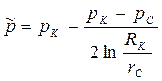 (92)
(92)
| 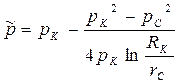 (93)
(93)
|
| Время движения отмеченных частиц | 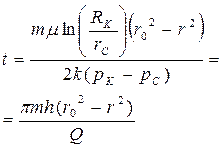 (94)
(94)
|
 ________________ ________________
|
| Время движения частицы от контура до забоя Т | 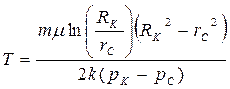 (95)
(95)
| 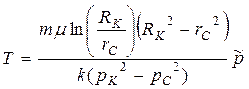 (96) (96)
|
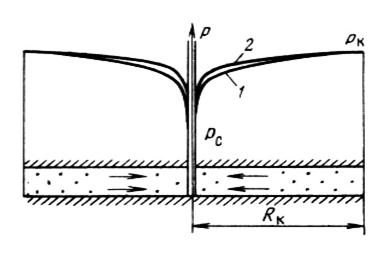 |
Рис.2 Кривые распределения давления в плоскорадиальном потоке:
1 – для жидкости, 2 – для газа.
Для несжимаемой жидкости давление меняется вдоль координаты r по логарифмическому закону (Рис. 2, кривая 1). Вращение кривой p (r) в пространстве вокруг оси скважины образует поверхность, называемую воронкой депрессии.
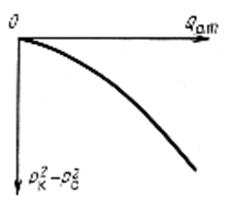 Зависимость дебита от перепада давления
Зависимость дебита от перепада давления  называется индикаторной линией. В потоке жидкости по закону Дарси индикаторная линя – прямая (Рис. 3).
называется индикаторной линией. В потоке жидкости по закону Дарси индикаторная линя – прямая (Рис. 3).
Вид индикаторной линии не зависит от геометрии потока и определяется только законом фильтрации. Отношение массового дебита скважины Q m к перепаду давления D р называется коэффициентом продуктивности скважины k. Рис. 3.
Из (60) следует, (для жидкости):
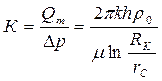 , (97)
, (97)
коэффициент продуктивности определяется в результате исследования скважины при установившихся отборах. Если исследования скважины выполнены при 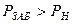 (
(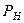 - давление насыщения нефти газом), то по тангенсу угла наклона коэффициент продуктивности скважины
- давление насыщения нефти газом), то по тангенсу угла наклона коэффициент продуктивности скважины
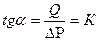 , (98)
, (98)
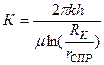 , (99)
, (99)
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 1884; Нарушение авторских прав?; Мы поможем в написании вашей работы!