Дифференциальное уравнение движения 4 страница

где С – постоянная интегрирования.

Потенциал в окрестности скважины – стока пропорционален логарифму расстояния r от стока (центра скважины). Пр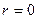и и 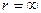функция 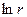обращается в бесконечность, поэтому потенциал в этих точках теряет смысл.

Потенциал точечного стока в пространстве, движение вблизи такого стока будет радиально-сферическим. Поэтому скорость фильтрации

, (224)

откуда

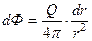, (225)

и потенциал точечного стока в пространстве

. (226)

Для потенциала точечного источника знак дебита в формуле (226) меняется на противоположный.

Распределение давления и потенциал в установившихся потоках несжимаемой жидкости описывается уравнением Лапласа, которое для плоских течений имеет вид

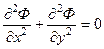(227)

Математический смысл метода суперпозиции заключается в том, что если имеется несколько фильтрационных потоков с потенциалами Ф₁(x,y), Ф₂(x,y),….., Ф_n(x,y), каждый из которых удовлетворяет уравнению Лапласа, т.е.

т. е.

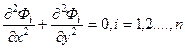, (228)

то и сумма (где С_i – произвольные постоянные) также удовлетворяют уравнению Лапласа (227).

Гидродинамический смысл метода суперпозиции состоит в том, что изменение пластового давления и потенциала в любой точке пласта, вызванное работой каждой скважины, подчиняется так, как если бы данная скважина работала в пласте одна, совершенно независимо от других скважин; затем эти независимо определенные для каждой скважины изменения давления и потенциала в каждой точке пласта алгебраически суммируются. Суммарная скорость фильтрации находится как сумма векторов скоростей фильтрации, вызванных работой каждой скважины по правилам сложения векторов.

Пусть на неограниченной плоскости расположено n источников и стоков. Потенциал каждого из них в точке М определяется по формуле (223):

; , (229)

где - расстояния от первого, второго, …. n – го стоков до точки М; 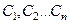- постоянные.

Каждая из функций удовлетворяет уравнению Лапласа. Тогда сумма потенциалов

, (230)

также удовлетворяют уравнению Лапласа. Физически это означает, что фильтрационные потоки от работы каждого источника или стока накладываются друг на друга. В этом и заключается принцип суперпозиции, или сложения течений.

Приток жидкости к группе скважин в пласте с удаленным

контуром питания.

Дано: Горизонтальный пласт, толщиной h; А1, А2,…,Аn – группа скважин с радиусом rci, которые работают с различными забойными потенциалами Фci,

i = 1,2,…,n, Фк – потенциал на контуре питания. Расстояние между центрами

i – й и j- й скважин известны. Контур питания находится далеко от всех скважин, поэтому можно приближенно считать, что расстояние от всех скважин до всех точек контура одно и тоже и равно .

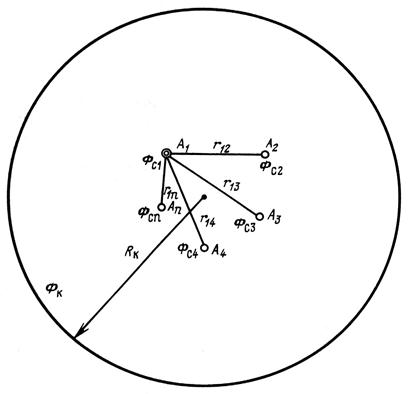
Рис. 15.

Схема группы скважин в пласте с удаленным контуром питания.

Определить: дебит каждой скважины и скорость фильтрации в любой точке пласта.

Решение: Потенциал в любой точке пласта М определим из выражения (230)

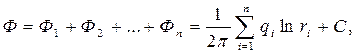
где - дебит скважины – стока, приходящейся на единицу толщины пласта; r1,r2,…,r n – расстояние от первого, второго, n – го стоков до точки М; С1, С2,…,Сn - постоянные. С = С1 + С2 +Сn.

Точку М последовательно поместим на забой каждой скважины, получим выражения забойного потенциала на них в виде

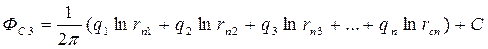(231)

Дополнительное уравнение получаем, поместим точку М на контур питания:

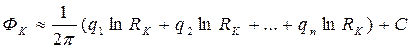(232)

Вычитая почленно каждое из уравнений (231) из (232), исключив постоянную С получим систему из n уравнений, из которой можно определить дебиты скважин q1,q1,…,qn, если заданы забойные и контурные потенциалы Фс1, Фс2,…, Фcn, Фк. Таким образом, можно решить обратную задачу определения потенциалов по известным дебитам qi (i = 1,2,…,n).

Имеем:

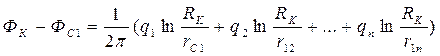
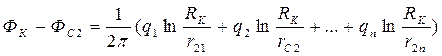
(233)

Чтобы определить физический смысл полученных соотношений в уравнениях (233) перейдем от потенциалов к давлениям, используя формулу (219), получаем:

;

……………………………………………………..

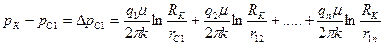. (224)

полная потеря давления на стенке любой скважины равна сумме потерь давления от работы всех скважин:

. (225)

Скорость фильтрации в любой точке пласта М определяется как геометрическая сумма скоростей фильтрации, вызванных работой каждой скважины и направлена по радиусу от точки М к данной скважине – стоку:

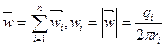. (226)

Приток жидкости к скважине в пласте с прямолинейным

контуром питания.

В полубесконечном пласте с прямолинейным контуром питания, на котором потенциал равен Фк, работает одна добывающая скважина А с забойным потенциалом Фс.

Определить: дебит скважины q, потенциал и скорость фильтрации в любой точке пласта.

Рис. 16. Схема притока жидкости к скважине в пласте с прямолинейным контуром питания.

Для решения этой задачи используем метод отображения источников и стока. Зеркально отобразим скважину – сток А относительно контура питания и дебиту скважины – изображения 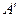припишем противоположный знак, т.е. будем считать ее скважиной-источником.

Рассмотрим в бесконечном пласте совместную работу двух скважин: скважины стока А с дебитом q и скважины – источника А¢ с дебитом q. Потенциал в любой точке М, находящейся на расстоянии r1, от скважины А и r2 от скважины А¢:

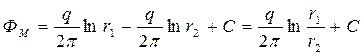(227)

Потенциал на контуре питания можно выразив подставив в 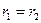, в результате чего получаем:

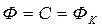(228)

Из (227) с учетом (228) потенциал на забое скважины А 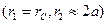можно выразить следующим образом:

(229)

Из (229) выражение для дебита скважины А (для единицы толщины пласта), получим:

(230)

Если бы контур питания был окружность радиуса а, то дебит скважины был бы равен (по формуле Дюпюи):

(231)

Из (227) с учетом (228) определим потенциал в любой точке М:

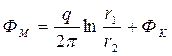. (232)

скорость фильтрации равна геометрической сумме скоростей фильтрации, вызванных работой реальной скважины – стока А и фиктивной скважины – источника 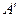, , 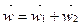где и направлена к скважине А;

и направлена от скважине .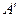

Приток жидкости к бесконечным цепочкам и кольцевым батареям скважин

На примере притока жидкости к нескольким рядам или кольцевым батареям скважин можно ознакомиться с широко применяемые при проектировании разработки нефтяных месторождений методом эквивалентных фильтрационных сопротивлений, предложенным Борисовым и основанным на аналогии движения жидкости в пористой среде с течением электрического тока в проводниках.

Для понимания данного вопроса рассмотрим задачу о притоке жидкости к одной бесконечной цепочке скважин, расположенных на расстояниях 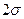друг от друга и на расстоянии L от прямолинейного контура питания. При этом условимся, что на контуре питания будет постоянный потенциал 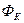, а на забоях скважин - . Определим дебит каждой скважины и суммарный дебит n скважин в цепочке.

Таким образом цепочка скважин-стоков отображается зеркально относительно контура питания в скважины-источники, и рассматривается интерференция двух цепочек скважин в неограниченном пласте.

Данная задача решается методом суперпозиции. Результаты решения показывают, что на расстоянии от контура до половины расстояния между скважинами движение жидкости практически прямолинейное и падение потенциала на этом участке происходит по закону прямолинейной фильтрации.

Основное падение потенциала происходит вблизи скважины, где характер движения близок к радиальному. При этом дебит каждой скважины цепочки выражается следующей формулой:

, (233)

где 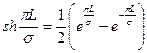- геперболический синус.

В случае, когда 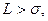величина 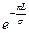очень мала и тогда .

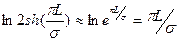Отсюда следует, что при дебит скважины определяется следующим образом:

. (234)

Введем обозначения

, ,

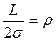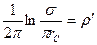формулу (234) представим в виде, аналогичном закону Ома.

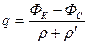. (235)

Величина 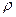по терминологии Ю.П. Борисова, называется внешним фильтрационным сопротивлением батареи, 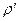- внутренним. Таким образом, приток жидкости к цепочке скважин можно представить схемой эквивалентных фильтрационных сопротивлений.

Аналогом объемного расхода служит сила тока, а аналогом разности фильтрационных потенциалов – разность электрических потенциалов. Суммарный дебит прямолинейной цепочки из n скважин

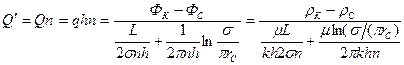. (236)

Из формулы (236) следует выражение для внешнего фильтрационного сопротивления цепочки: , которое представляет собой сопротивление потоку жидкости от контура питания до галереи длиной , расположенной на расстоянии L от контура питания, а внутреннее сопротивление 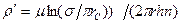выражает сопротивление, возникающее при подходе жидкости к скважинам в зоне радиусом , где фильтрация практически плоскорадиальная.

Лекция 9

Виды несовершенства скважин

Скважина называется гидродинамически совершенной, если она вскрывает продуктивный пласт на всю толщину и забой скважины открытый, т.е. вся вскрытая поверхность забоя является фильтрующей.

Если скважина с открытым забоем вскрывает пласт не на всю толщину h, а только на некоторую глубину b, то ее называют гидродинамически несовершенной по степени вскрытия пласта. при этом 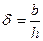называется относительным вскрытием пласта.

если скважина вскрывает пласт до подошвы, но сообщение с пластом происходит только через специальные отверстия в обсадной колонне и цементном камне или через специальные фильтры, то такую скважину называют гидродинамически несовершенной по характеру вскрытия пласта.

Встречаются скважины и с двойным видом несовершенства – как по степени, так и по характеру вскрытия пласта. тепень вскрытия пласта имеют очень важное значение при разработке месторождений нефти и газа, так как они определяют фильтрационные сопротивления, возникающие в призабойной зоне, и, в конечном итоге, производительность скважин.

Приток жидкости к несовершенным скважинам

при выполнении закона Дарси.

Приток жидкости к несовершенной скважине даже в горизонтальном однородном пласте постоянной толщины перестает быть плоскорадиальным. строгое математическое решение задачи о притоке жидкости к несовершенной скважине в пластах конечной толщины представляет большие трудности.

Путем подбора интенсивности расходов q и используя метод суперпозиции действительных и отображенных стоков, М. Маскет получил формулу для дебита гидродинамически несовершенной по степени вскрытия пласта скважины:

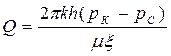, (237)

где

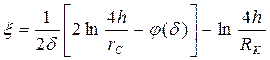(238)

функция степени вскрытия пласта - имеет следующее аналитическое выражение:

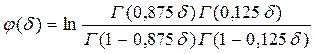, (239)

где - интеграл Эйлера второго рода, называется гамма – функцией, для которой имеются таблицы в математическом справочнике.

При d = 1, т.е. пласт вскрыт полностью, (237) переходит в формулу Дюпюи для плоскорадиального потока.

Кроме того, для расчета несовершенной по степени вскрытия пласта скважины используется более простая формула, чем (237) М. Маскета, предложенная И. Козени:

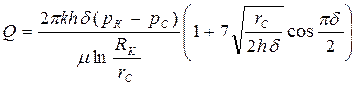(240)

Гидродинамическое несовершенство скважины характеризуется коэффициентом совершенства скважины, 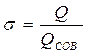, где Q – дебит несовершенной скважины, Qсов – дебит совершенной скважины.

Широкое распространение получил метод расчета дебитов несовершенных скважин, основанный на электрогидродинамической аналогии фильтрационных процессов.

Дебит гидродинамически несовершенной скважины подсчитывается по формуле

, (241)

где С = С1 + С2 – дополнительное фильтрационное сопротивление, вызванное несовершенством скважины по степени вскрытия пласта (С1) и характеру вскрытия (С2).

Измеряя разность потенциалов и силу тока, можно подсчитать сопротивление по закону Ома, сделать пересчет на фильтрационное сопротивление и определить дополнительное фильтрационное сопротивление.

В. И. Щуровым были проведены такие экспериментальные исследования, в ходе которых им были определены дополнительные фильтрационные сопротивления С1 и С2 для различных видов несовершенства скважин и построены соответствующие графики.

Выражение дополнительного фильтрационного сопротивления получено И. А. Чарным с использованием формулы Маскета (237) в виде

, (242)

где j(d) определяется по формуле (239) или по графику.

А. М. Пирвердян получил для коэффициента С1 следующее выражение

(243)

Сравнив дебиты совершенной скважины (формула Дюпюи) и несовершенной скважины (241), получим выражения коэффициента совершенной скважины в следующем виде:

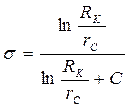. (244)

Иногда бывает удобно ввести понятие о приведенном радиусе скважин , т.е. радиусе такой совершенной скважины, дебит которой равен дебиту данной несовершенной скважины:

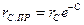. (245)

Тогда (241) можно заменить следующей формулой:

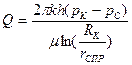. (246)

Лекция 10

Двухфазная фильтрация несмешивающихся жидкостей.

Проектирование и анализ разработки нефтяных и газовых месторождений проводится с использованием данных по исследованию течения в пористой среде нескольких жидкостей, т.е. рассматривается многофазная фильтрация.

Формирование залежей происходит в результате оттеснения из пластов-коллекторов первоначально находившейся там воды. поэтому вместе с нефтью и газом в коллекторах содержится некоторое количество так назаваемой остаточной воды, а кроме того, многие продуктивные пласты заполнены нефтью и газом лишь в верхней купольной части, а нижележащие зоны заполнены краевой водой. Самые верхние части нефтяных залежей содержат газ, образующий так называемые газовые шапки, которые могут как существовать изначально, так и появиться в процессе разработки залежи. Таким образом, даже в неразбуренном пласте может находиться несколько отдельных подвижных фаз.

На вытеснении нефти водой или газом основана технология ее извлечения из недр при разработке месторождений.

Рассмотрим процесс вытеснения, происходящий в прямолинейном тонком горизонтальном образце (Рис. 18), представленной однородной и изотропной средой.

В рассматриваемый образец первоначально заполненный нефтью, через сечение x = 0 закачивается вода.

Опыты показывают, что расход каждой фазы растет с увеличением насыщенности и градиента давления. Рис. 18. Схема прямолинейно параллельного вытеснения нефти водой.

В этом случае закон фильтрации каждой фазы можно представить в виде обобщенного закона Дарси в дифференциальной форме:

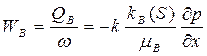(247)

(248)

Здесь Wв, Qв и Wн, Qн – скорости фильтрации и объемные расходы соответственно воды и нефти, mв, mн – коэффициенты динамической вязкости фаз, kв(S) и kн(S) – относительные фазовые проницаемости, S = Sв – водонасыщенность. Sв + Sн = 1

Исключим градиент давления 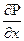, поделив почленно одно на другое уравнения (247) на (248):

, (249)

где .

Применив к (249) правило производных пропорций и использовав соотношения Wв + Wн = W(t) или Qв + Qн = Q(t), (*) и использовав (249) получим:

(250)

Обозначим

(251)

Из предыдущего равенства найдем:

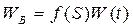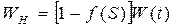и (252)

Функция насыщенности f(S), называется функцией распределения потоков фаз или функцией Бакли – Леверетта.

Из (252) следует, что f(S), представляющая отношение скорости фильтрации (или расхода) вытесняющей фазы (воды) и суммарной скорости W (или расхода Q), равна объемной доле воды в суммарном потоке двух фаз. Функция f(S) определяет полноту вытеснения и характер насыщенности по пласту. Задача повышения нефти – и газоконденсатоотдачи в значительной степени сводится к применению таких воздействий на пласт, которые, в конечном счете изменяют вид f(S) в направлении увеличения полноты вытеснения.

Из (174) видно, что функция f(S) полностью определяется относительными фазовыми проницаемостями (Рис. 19).

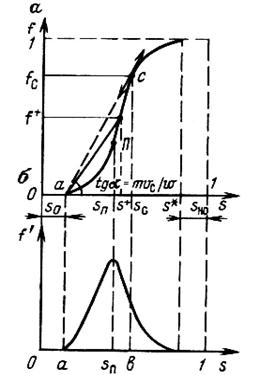С ростом водонасыщенности f(S) моно

тонно возрастает от 0 до 1. Характерная

особенность графика f(S) – наличие точки

перегиба П с насыщенностью Sп, участков

вогнутости и выпуклости, где вторая про –

изводная f¢¢(S) соответственно больше и

меньше нуля. Эта особенность в большей

степени определяет специфику фильтра –

ционных задач вытеснения в рамках

модели Бакли – Леверетта.

Рис. 19. Зависимость объемной доли вытесняющей фазы (воды) в потоке f(а) и ее производной (б) от насыщенности.

Уравнение

(253)

Уравнение (253), является дифференциальноым уравнением только относительно насыщенности. Изменение насыщенности во времени по пласту можно получить в результате решения уравнения (253) независимо от распределения давления р(x, t). Уравнение (253) является уравнением Бакли – Леверетта. Для нахождения распределения насыщенности к уравнению (253) нужно добавить начальное и граничное условия:

при t = 0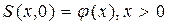

при x = 0 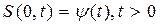(254)

Первое из уравнений (254) означает, что в момент времени t = 0 (до начала процесса вытеснения) в пласте имеется некоторое известное распределение насыщенности S вытесняющей фазы, определяемое функцией j(x). Согласно второму условию (254), при t > 0 в пласт через нагнетательную галерею, расположенную на “линии” x = 0, закачивается вытесняющая жидкость (вода), насыщенность которой при x = 0 меняется со временем по заданному закону y(t). В некоторых случаях можно считать, что

(255)

Это – случай кусочно-постоянных начальных данных, имеющий важное значение для практических приложений. Величина начальной водонасыщенности 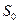влияет на процессы заводнения и определяет структуру зоны вытеснения.

В гидродинамических расчетах часто удобно пользоваться эмпирическими зависимостями значений относительной фазовой проницаемости от насыщенности, полученными из экспериментальных данных. Рассмотрим эмпирические формулы, полученные Чень-Чжун-Сяном, которые можно принять при оценочных расчетах.

1. Для воды и нефти (s – водонасыщенность):

;

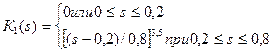; (256) 2. Для воды и газа (s-газонасыщенность):

;

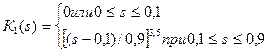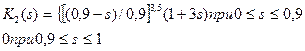; (257)

Решение уравнения Бакли – Леверетта.

В процессе нагнетания воды в пласт ее насыщенность будет меняться со временем вдоль направления движения x. Связь между S, x и t можно записать в функциональной форме S = S (x, t) или, что эквивалентно, в дифференциальной форме

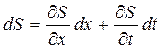. (258)

Рассмотрим на плоскости 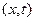такие линии , вдоль которых насыщенность принимает заданное постоянное значение. Эти линии называются изосатами (т.е. линии постоянной насыщенности).

Для любого заданного значения можно установить такую связь между x и t, что удовлетворяется уравнение S = S (x, t) = const или эквивалентное дифференциальное уравнение.

Решим совместно два уравнения:

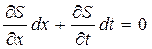(259)

Решение системы уравнений (259) дает соотношение между x и t в дифференциальной форме.

Из решения уравнений (259) находим:

(260)

Производная dx/dt вычисляется при постоянном значении S, т. е.

dx/dt = ¶x/¶t.

Найдем положение х (после интегрирования 260) заданного значения насыщенности как функцию времени:

, (261)

где хо – значения координат с начальной водонасыщенностью So при t = 0.

Таким образом, уравнения (260) и (261)

dx/dt = w/mf¢(s)

и

x(s) = w/mf¢(s)t + xo

можно использовать для расчета скорости и координаты данного значения насыщенности в области непрерывного профиля, и уравнения

(262)

индексом “с” обозначены величины, относящиеся к фронту (скачку) насыщенности, а , выражение (262) задает скорость Vc распространения фронта насыщенности и известно как условие на скачке.

Равенство (262) имеет простой геометрический смысл: скорость скачка Vc пропорциональная тангенсу угла наклона к оси S секущей, соединяющей точки кривой f(S), имеющие абсциссы с коэффициентом пропорциональности w/m.

Если насыщенности по обе стороны фронта постоянны, уравнение (262) можно проинтегрировать и найти положение фронта как функцию времени:

, (263)

где хco – положение скачка при t = 0 (хco = 0).

При помощи (262) и (263) можно найти скорость и положение скачка насыщенности.

Приведем простой способ графического построения профиля насыщенности, который состоит в следующем (Рис. 19):

Дата добавления: 2014-11-20