Тема: Методы проекций

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ И ИНЖЕНЕРНАЯ ГРАФИКА

Лекционный комплекс для студентов

Специальности 5В071300 - Транспорт, транспортная техника и технологии

Костанай, 2011

Начертательная геометрия – это наука, в которой пространственные формы предметов изучаются при помощи их графических изображений на плоскости. Как наука, она дает теоретическое обоснование методов и способов построения изображений геометрических тел и их элементов.

Основные задачи начертательной геометрии сводятся к следующим двум:

1. изучение способов построения изображений пространственных форм предметов на плоскости;

2. изучение способов решения пространственных геометрических задач при помощи этих изображений.

Пространственные задачи делят на позиционные и метрические. Позиционными называются задачи на определение взаимного положения геометрических фигур относительно друг друга. Метрическими – задачи на определение метрических свойств геометрических фигур, т. е. на определение их размеров или построение проекций геометрических фигур по заданным размерам и положению в пространстве.

Изучающий начертательную геометрию – это переводчик. Для него table – это стол, а стол - это table. По изображениям он должен представлять оригинал, а зная что-то об оригинале, понять, как это интерпретируется в изображении. Решая задачу по начертательной геометрии, приходится все время переводить с языка оригиналов, натуры, языка стереометрии на язык чертежа, изображений, язык планиметрии и наоборот, все время держать в голове соответствие: на картинке – на самом деле, на самом деле – на картинке. При этом картинку мы видим, а что на самом деле – должны представить, вообразить, «увидеть» мысленно.

Но этот перевод, разумеется, не самоцель, а только средство. Цель – решить изображённую на плоском чертеже пространственную задачу. Поэтому нужно вначале представить, вообразить, «увидеть» мысленно как решается эта стереометрическая, трёхмерная задача. А уж потом переводить это решение на планиметрический язык, на язык двухмерного чертежа, на язык проекций.

Стереометрические задачи, решаемые в начертательной геометрии – это задачи конструктивные, задачи на построение (в отличие задач на доказательство или на вычисление). Вначале следует составить (в голове) план возведения стереометрической конструкции, «увидеть» последовательность приводящих к цели действий в пространстве, алгоритм решения трёхмерной задачи, а затем переходить к реализации этих действий на чертеже, к переводу этого плана-алгоритма на язык изображений.

Конкретные трудности при освоении начертательной геометрии иллюстрируют две задачи-шутки: - что изображено на рисунках 1 и 2? Ответ: милиционер на посту и мексиканец на велосипеде (вид сверху). Чтобы это «увидеть», нужно чуть-чуть напрячь пространственное воображение, включить свою геометрическую интуицию. Трудности испытывают обычно те, кто видит на этих рисунках только окружности и прямые и не задумывается об их проекционном смысле, о том, что же эти линии изображают, кто видит только планиметрию и забывает о ее переводе на язык стереометрии. В переводе окружности на рис. 1-это фуражка и козырёк, а прямые-погоны, на рис.2 окружности изображают шляпу, а прямые-колёса велосипеда. По рис.1 можно догадаться, что на нем изображен милиционер, но сказать какого он роста принципиально невозможно. Чертеж на рис. 1 соответствует не одному оригиналу, а многим, этот чертеж необратим, он дает существенную информацию об оригинале, но, к сожалению, не всю информацию. Точный, однозначный перевод здесь невозможен. Это «стол» имеет много значений.

Рис. 1 Рис. 2

Изучение начертательной геометрии основано на методе проекций. Метод проекций заключается в том, что через определённые точки пространственного предмета проводят воображаемые прямые до пересечения с какой-либо плоскостью и соединяют полученные точки соответствующими линиями (прямыми и кривыми). На плоскости получается изображение предмета в виде плоской фигуры, состоящей из определённого сочетания точек и линий, при рассмотрении которых создаётся представление об этом предмете – его форме и положении в пространстве.

Процесс линейного отображения точек пространства на плоскости называется проецированием. Плоскость, на которой построено изображение, - плоскостью проекций. Воображаемые прямые,.. с помощью которых строится изображение, - проецирующими лучами. Геометрически закономерное изображение предмета, полученное проецированием на плоскость, называется проекцией. Рисунки, фотографии, чертежи, тени, падающие от освещённых предметов, -всё это примеры проекций каких-либо предметов пространства.

Проецируемые точки, линии, фигуры, предметы пространства будем называть оригиналами.

Основными видами проекций, изучаемых в начертательной геометрии, являются центральные и параллельные.

Метод проецирования заключается в том, что любая из множества точек пространства может быть спроецирована с помощью проецирующих лучей на любую поверхность (плоскость).

Возьмем некоторую плоскость пространства π ´, называемую плоскостью проекций; точку S вне этой плоскости (центр проекций) и произвольную точку пространства А (рисунок 3).

Проведем луч SА (проецирующий луч) до пересечения с плоскостью π ´ - получим точку А ´ - изображение или проекцию точки А на плоскость π ´.

Центр проекций S и плоскость проекций p¢ образуют аппарат проецирования.

В зависимости от положения центра проецирования по отношению к плоскости проекций проецирование может быть или центральным (коническим) или параллельным (цилиндрическим).

рисунок 3

При центральном проецировании проецирующие лучи выходят из одной точки – центра проецирования S, который находится на определенном (конечном) расстоянии от плоскости проекций.

Чтобы получить центральную проекцию фигуры на плоскость, пользуются связкой проецирующих лучей (рисунок 4) – SА, SВ, SС. Треугольник А´ В´ С´ - центральная проекция треугольника АВС.

Рисунок 4

Центральное проецирование обладает большой наглядностью, так как оно соответствует зрительному восприятию предметов. Основной его недостаток – сложность в определении размеров предмета по его изображению.

Параллельное проецирование можно рассматривать как частный случай центрального, когда центр проецирования удален в бесконечность. При этом проецирующие лучи параллельны между собой (рисунок 5). При параллельном проецировании необходимо задать направление проецирования – s и плоскость проекций p¢.

Построение параллельной проекции предмета отличается от построения его центральной проекции только тем, что при параллельном проецировании проецирующие лучи параллельны между собой, а при центральном – выходят из одной точки.

Рисунок 5

В зависимости от направления проецирующих лучей по отношению к плоскости проекций параллельное проецирование может быть косоугольным – проецирующие лучи не перпендикулярны к плоскости проекций (рисунок 5) или прямоугольным – проецирующие лучи перпендикулярны к плоскости проекций (рисунок 6).

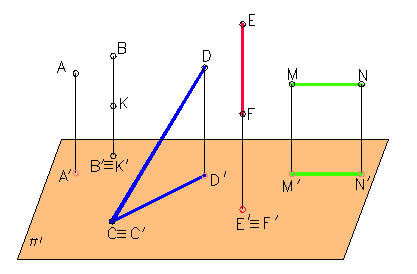
рисунок 6

Прямоугольное (ортогональное) проецирование находится в основе выполнения почти всех чертежей, поэтому в дальнейшем будем рассматривать только этот вид проецирования.

Понятие об эпюре Монжа.

Г.Монж предложил следующую схему получения обратимого чертежа: оригинал проецируется прямоугольно на две взаимно

перпендикулярные плоскости p₁ и p₂, называемые фронтальной и горизонтальной плоскостями проекций. Они разделяют пространство на четыре подпространства, называемые четвертями. На рис. 7,а четверти пронумерованы римскими цифрами. Плоскость p₂ совмещается с плоскостью p₁ путем вращения ее вокруг оси Ох. Полученный плоский чертеж называется эпюром Монжа. Эпюр – французское слово «epure», переводится на русский язык «Чертеж».

Чертеж точки

Рисунок 7

Точка может находиться в одной из четвертей. Если точка А расположена в первой четверти, то фронтальная проекция А₁ этой точки находится выше оси Ох (рис. 4.1,б) и горизонтальная проекция А₂ – ниже. (А₁А₂) Ç (Ох)=А_х – основная проекция точки А. (А₁А₂) ^ х. Линия связи располагается перпендикулярно к оси проекций Ох. Точка В расположена во второй четверти, поэтому обе проекции В₁ и В₂ находятся выше Ох. Если точка С расположена в третьей четверти, то фронтальная ее проекция С₁ будет находиться ниже, а горизонтальная проекция С₂ выше оси Ох. Если точка С расположена в третьей четверти, то фронтальная ее проекция С₁ будет находиться ниже, а горизонтальная проекция С₂ выше оси Ох. Точка расположена в четвертой четверти, поэтому обе проекции и находятся ниже Ох. Если фронтальная, горизонтальная и осевая проекции совпадают, то точка принадлежит оси проекции. Например: ; ; .

Изучая расположение фронтальной и горизонтальной проекций точки, можно определить в какой четверти расположена соответствующая точка. Если фронтальная проекция расположена выше, а горизонтальная проекция ниже оси проекций Ох, то точка находится в первой четверти. Если, наоборот, фронтальная проекция ниже и горизонтальная проекция выше Ох, то точка расположена в третьей четверти. Если обе проекции точки находятся выше оси Ох, то соответствующая точка расположена во второй четверти, а если, наоборот, обе проекции ниже Ох,то в четвертой четверти.

Рисунок 8

Зная координаты точки, можно построить эпюр точки и, наоборот по чертежу точки можно определить координаты точки. Для построения чертежа точки М (х,у,z) проводим горизонтальную прямую,которую принимаем за ось Ох, на которую отложив отрезок , равный х – абсциссе точки М. Через точку проводим прямую перпендикулярно к Ох, на которую отложив отрезок 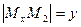вниз, получим

горизонтальную проекцию 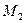точки М, и отложив отрезок вверх – фронтальную проекцию точки М (рис. 8).

Рисунок 9

Чертеж прямой

Прямая определяется двумя точкам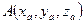и и . Для получения чертежа прямой, проходящей через точки А и В, по координатам определяем фронтальные и , горизонтальные и 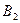проекции этих точек (рис.9).

Чертеж плоскости

Плоскость определяется: тремя точками, не лежащими на одной прямой, точкой и прямой, не проходящей через эту точку; двумя параллельными прямыми; двумя пересекающимися прямыми. На эпюре плоскость изображается фронтальными и горизонтальными проекциями геометрических элементов, определяющих ее (рис.10). Плоскость

может быть задана двумя проекциями любой заведомо плоской фигуры. Наиболее наглядным способом изображения плоскости является задание ее следами.

Рис 4.4

Рисунок 10

Основная литература: 1.7.1 (5..12), 1.7.1 (17…23)

Дополнительная литература: 1.7.17 (5..15), 1.7.10 (4…20),1.7.11 (9..12), 1.7.17 (300…315), 1.7.10 (203…212), 1.7.11 (234…258).

Контрольные вопросы:

1. Что изучает предмет начертательной геометрии?

2. Назовите виды проецирования и основные их различия.

3. Назовите элементы аппарата проецирования центральной и параллельной проекций.

4. В чем отличие прямоугольного и косоугольного проецирования?

5. Назовите основные свойства параллельного проецирования?

6. Является ли параллельное проецирование частным случаем центрального и почему?

7. Поясните необходимость решения обратной задачи. Что такое обратимость чертежа?

Дата добавления: 2014-11-20