
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема: Некоторые способы преобразования чертежа
|
|
|
|
ОСНОВНЫЕ ПОЗИЦИОННЫЕ ЗАДАЧИ
Основными позиционными задачами называются задачи, в которых определяются взаимное расположение точек, прямых и плоскостей. Существует всего 6 основных позиционных задач: взаимное расположение точек; взаимное расположение точки и прямой; взаимное расположение прямых; взаимное расположение точки и плоскости; взаимное расположение прямой и плоскости; взаимное расположение плоскостей. Различают позиционные задачи на принадлежность, параллельность и пересечение.
5.2.Построение точки пересечения прямой и плоскости
В начале рассмотрим взаимное расположение прямой и проецирующей плоскости. Здесь возможны три случая: вырожденная в прямую проекция плоскости и соответствующая проекция прямой могут совпадать, располагаться или пересекаться. В зависимости от этого прямая принадлежит плоскости, располагается ей параллельно или они пересекаются. На рис. 6.2 изображены фронтально проецирующая плоскость  и три прямые
и три прямые 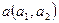 ,
,  и
и 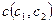 .
.  , поэтому прямая
, поэтому прямая 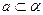 .
. 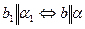 ;
;  .
.
Найти точку пересечения прямой и плоскости – это означает, что нужно определить такую точку, принадлежащую данной прямой, и проекции которой будут находиться в соответствии, установленном данной плоскостью.
Пусть требуется построить проекции точки пересечения прямой 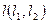 и плоскости
и плоскости  (рис. 17).
(рис. 17).

Рисунок 17
Отнесем прямую 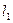 полю фронтальной проекции плоскости
полю фронтальной проекции плоскости  и обозначим через
и обозначим через 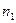 . Определим
. Определим
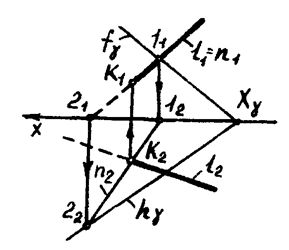
Рисунок 18
прямую 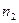 , родственную прямую
, родственную прямую 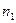 в соответствии, установленном плоскостью
в соответствии, установленном плоскостью  . Таким образом, задача сводится к определению взаимного расположения прямых
. Таким образом, задача сводится к определению взаимного расположения прямых 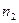 и
и 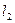 . Если
. Если 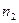 =
= 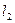 , то
, то 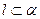 ;
; 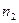 ||
|| 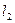 , то
, то  . На нашем примере
. На нашем примере 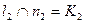 . С помощью линии связи, проведенной через точку
. С помощью линии связи, проведенной через точку 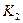 , определена точка
, определена точка 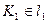 . Точка
. Точка 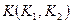 является искомой точкой
является искомой точкой
пересечения прямой  и плоскости
и плоскости  :
: 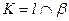 . Невидимые на эпюре части прямой проведены штриховой линией. Для установления видимости на фронтальной проекции использованы фронтально конкурирующие точки 1 и 3, с на горизонтальной проекции – горизонтально конкурирующие точки 4 и 5.
. Невидимые на эпюре части прямой проведены штриховой линией. Для установления видимости на фронтальной проекции использованы фронтально конкурирующие точки 1 и 3, с на горизонтальной проекции – горизонтально конкурирующие точки 4 и 5.
Аналогично определяется точка пересечения прямой  и плоскости
и плоскости 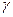 , заданной своими следами (рис. 18). Прямой
, заданной своими следами (рис. 18). Прямой 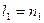 , отнесенной фронтальной проекции плоскости
, отнесенной фронтальной проекции плоскости 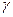 , соответствует прямая
, соответствует прямая 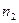 ; прямая
; прямая 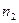 проходит через точки
проходит через точки 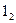 и
и 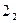 . Точка пересечения прямых
. Точка пересечения прямых  и
и  будет искомой точкой:
будет искомой точкой: 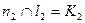 ;
; 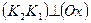 ;
;  ;
; 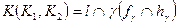 . Часть прямой
. Часть прямой  , которая начинается из точки
, которая начинается из точки 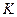 и расположена ниже плоскости
и расположена ниже плоскости 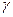 , будет невидимой.
, будет невидимой.
Линия пересечения двух плоскостей
На рис. 19 изображены две плоскости 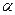 и
и  , первая из которых задана параллельными прямыми
, первая из которых задана параллельными прямыми 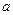 и
и 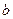 , а вторая – пересекающимися прямыми
, а вторая – пересекающимися прямыми 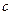 и
и  . Требуется установить взаимное расположение этих плоскостей
. Требуется установить взаимное расположение этих плоскостей 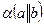 и
и 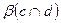 .
.
Здесь мы имеем два родственных соответствия, порождаемые соответственно плоскостями 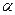 и
и  . Нам надо определить общую прямую этих двух родственных соответствий. Проведем произвольную прямую
. Нам надо определить общую прямую этих двух родственных соответствий. Проведем произвольную прямую  и отнесем ее плоскости
и отнесем ее плоскости 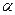 . Тогда ей соответствует прямая
. Тогда ей соответствует прямая 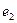 в родстве, определяемым первой плоскостью. Затем отнесем прямую
в родстве, определяемым первой плоскостью. Затем отнесем прямую  второй плоскости и обозначим
второй плоскости и обозначим 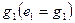 . Находим соответствующую ей прямую
. Находим соответствующую ей прямую 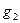 в родстве, установленном второй плоскостью. Рассмотрим взаимное расположение двух прямых
в родстве, установленном второй плоскостью. Рассмотрим взаимное расположение двух прямых 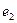 и
и 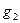 . Возможны три случая:
. Возможны три случая:
1) 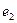 =
= 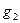 ; тогда плоскости
; тогда плоскости 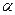 и
и  совпадают (
совпадают (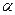 =
=  );
);
2) 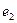 Ç
Ç 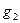 =
= 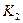 ; тогда точка К принадлежит линии пересечения плоскостей:
; тогда точка К принадлежит линии пересечения плоскостей:  ;
;
3) 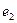 ||
|| 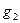 .
.
В первом случае задача уже решена. Если имеет место второй или третий случай, следует повторить построение, изменив
положение прямой  на
на  . В случае, когда
. В случае, когда  необходимо выполнить условие
необходимо выполнить условие  не параллельна
не параллельна  . Находим прямую
. Находим прямую  плоскости
плоскости  , и прямую
, и прямую  , относя прямую
, относя прямую 
|
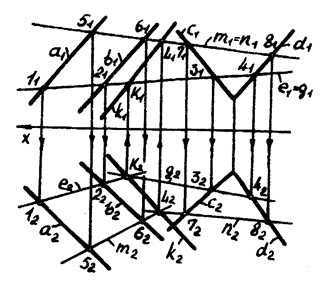 | 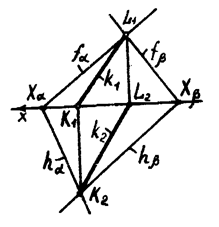 | ||
Рисунок 19
плоскости  . Теперь возможны два случая: 1) прямые
. Теперь возможны два случая: 1) прямые 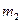 и
и 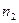 параллельны, тогда
параллельны, тогда  ; 2) прямые
; 2) прямые 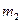 и
и 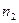 пересекаются в точке
пересекаются в точке 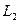 . Точка
. Точка  принадлежит линии пересечения плоскостей:
принадлежит линии пересечения плоскостей: 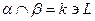 . Во втором случае данные плоскости пересекаются по прямой
. Во втором случае данные плоскости пересекаются по прямой  , которая проводится через точки
, которая проводится через точки 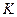 и
и  или через точку
или через точку  параллельно прямым
параллельно прямым  и
и 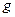 (если
(если  ).
).
Пример 3. Построить линию пересечения плоскостей 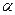 и
и  , заданных своими следами (рис.20).
, заданных своими следами (рис.20).
Решение. Точка пересечения  фронтальных следов плоскостей и точка пересечения
фронтальных следов плоскостей и точка пересечения 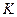 горизонтальных следов плоскостей являются общими точками заданных плоскостей.
горизонтальных следов плоскостей являются общими точками заданных плоскостей.
 ;
; 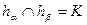 .
.
Поэтому прямая  , соединяющая точки
, соединяющая точки 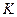 и
и  , является искомой линией пересечения:
, является искомой линией пересечения: 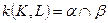 . Этот результат является частным случаем выше приведенной общей схемы. Здесь за
. Этот результат является частным случаем выше приведенной общей схемы. Здесь за 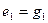 принимается ось
принимается ось 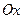 ; тогда
; тогда 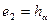 и
и 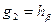 . За
. За 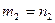 принимается также ось
принимается также ось 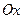 , в результате этого
, в результате этого 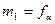 и
и  .
.
Метрические задачи. Преобразование чертежей
Перпендикулярность прямых
Теорема о прямоугольной проекции прямого угла имеет ряд важных следствий.
Следствие 1. Если из двух взаимно перпендикулярных прямых одна является фронталью, то их фронтальные проекции будут взаимно перпендикулярными. Наоборот, если из двух прямых одна является фронталью и их фронтальные проекции взаимно перпендикулярны, то они в пространстве также взаимно перпендикулярны.
Следствие 2. Если из двух взаимно перпендикулярных прямых одна является горизонталью, то их горизонтальные проекции располагаются под прямым углом. Наоборот, если из двух прямых одна является горизонталью и их горизонтальные проекции расположены под прямым углом, то они в пространстве также взаимно перпендикулярны. На рис. 5.2 представлены две пары взаимно перпендикулярных прямых 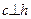 - пересекаются и
- пересекаются и 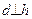 - скрещиваются.
- скрещиваются.
Перпендикулярность прямой и плоскости
 | 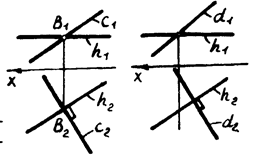 | ||
Известно, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости.
Рисунок 21 Рисунок 22
Теорема. Для того чтобы прямая была перпендикулярна плоскости, необходимо и достаточно, чтобы фронтальная проекция прямой была перпендикулярна фронтальной проекции фронтали, а горизонтальная проекция – горизонтальной проекции горизонтали этой плоскости.
Доказательство. Необходимость. Предположим, что прямая 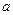 перпендикулярна плоскости
перпендикулярна плоскости  . Тогда прямая
. Тогда прямая 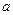 перпендикулярна каждой прямой, лежащей в этой плоскости, в том числе фронталям и горизонталям плоскости
перпендикулярна каждой прямой, лежащей в этой плоскости, в том числе фронталям и горизонталям плоскости 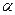 . Согласно следствию 1 фронтальная проекция
. Согласно следствию 1 фронтальная проекция  прямой
прямой 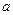 должна быть перпендикулярна фронтальной проекции
должна быть перпендикулярна фронтальной проекции  фронтали
фронтали  плоскости
плоскости 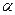 . Согласно следствию 2 горизонтальная проекция
. Согласно следствию 2 горизонтальная проекция 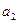 прямой
прямой 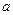 должна быть перпендикулярна горизонтальной проекции
должна быть перпендикулярна горизонтальной проекции  горизонтали
горизонтали  плоскости
плоскости 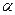 . Отсюда следует, что если
. Отсюда следует, что если 
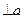 , то
, то  и
и 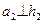 .
.


Рисунок 23 Рисунок 24
Достаточность. Предположим, что фронтальная проекция  фронтали
фронтали  плоскости
плоскости 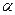 перпендикулярна фронтальной проекции
перпендикулярна фронтальной проекции  прямой
прямой 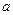 и горизонтальная проекция
и горизонтальная проекция  горизонтали
горизонтали  плоскости
плоскости 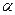 перпендикулярна горизонтальной проекции
перпендикулярна горизонтальной проекции 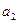 прямой
прямой 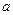 . Тогда согласно следствию 1 прямые
. Тогда согласно следствию 1 прямые 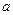 и
и  взаимно перпендикулярны и согласно следствию 2 прямые
взаимно перпендикулярны и согласно следствию 2 прямые 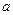 и
и  также взаимно перпендикулярны. Таким образом, выходит, что прямая
также взаимно перпендикулярны. Таким образом, выходит, что прямая 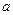 перпендикулярна двум пересекающимся прямым
перпендикулярна двум пересекающимся прямым  и
и  плоскости
плоскости 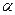 . Следовательно, прямая
. Следовательно, прямая 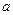 перпендикулярна и самой плоскости
перпендикулярна и самой плоскости 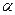 . Теорема доказана.
. Теорема доказана.
Перпендикулярность плоскостей
Плоскость 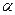 перпендикулярна плоскости
перпендикулярна плоскости  , если она проходит через прямую
, если она проходит через прямую 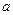 ,
,
перпендикулярную плоскости  , или она перпендикулярна прямой
, или она перпендикулярна прямой 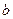 , лежащей в плоскости
, лежащей в плоскости  :
:  или
или  .
.
Через точку 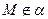 можно провести множество плоскостей
можно провести множество плоскостей 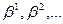 ,перпендикулярных плоскости
,перпендикулярных плоскости 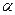 . Все эти плоскости проходят через перпендикуляр
. Все эти плоскости проходят через перпендикуляр 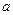 , опущенный из точки
, опущенный из точки 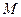 на плоскость
на плоскость 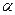 .
.
Построение новых проекций геометрических фигур по данным их проекциям называют преобразованием чертежа. Различают два подхода: изменение положения геометрических фигур относительно неподвижных плоскостей p1 и p2; введение дополнительной плоскости проекций при неподвижных геометрических фигурах. В первом подходе в зависимости от вида движения различают: способ плоскопараллельного перемещения, способ вращения вокруг проецирующей прямой и способ вращения вокруг прямой уровня. Во втором подходе наиболее важными являются способы замены плоскостей проекций и вспомогательного проецирования.
Способ плоскопараллельного перемещения
Плоскопараллельным перемещением фигуры называется такое ее движение, при котором все точки фигуры перемещаются в плоскостях, параллельных между собой. Рассматриваются перемещения, параллельные плоскости p1 или p2. Траектория движения не имеет значения, важно знать конечное положение. Как построить проекцию фигуры в конечном ее положении после некоторого плоскопараллельного перемещения? Для этого необходимо установить инварианты преобразования. Инвариантами преобразования называются такие правила, позволяющие по данным проекциям найти новую интересующую нас проекцию фигуры (инварианты – свойства, которые остаются без изменения).
Для определения инвариантов плоскопараллельного перемещения относительно горизонтальной плоскости проекций рассмотрим отрезок АВ в системе взаимно перпендикулярных плоскостей p1 и p2 (рис. 25,а). Точка А перемещается в горизонтальной плоскости a, а точка В – в плоскости b (a ïï b ïï p2). Пусть после некоторого движения отрезок АВ занимает новое положение [], где Î a и Î b. [ А1В1 ] и [ А2В2 ] –фронтальная и горизонтальная проекции отрезка АВ, [] и [] – фронтальная и горизонтальная проекции отрезка АВ после его перемещения до положения []. (АА2) bА ° и () b °. АА ° В и ° В – конгруэнтные прямоугольные треугольники, так как ï АВ ïïï и ï АА °ïï°ïï ab ï. Поэтому ï А ° В ïï°ï. Из чертежа видно, что ï А2В2 ïï А ° В ï и ïïï°ï.
 Для получения эпюр плоскость p2 вращением вокруг оси (Ох) совмещается с плоскостью p1 (рис. 25,б). Теперь сформулируем инварианты плоскопараллельного перемещения относительно p2:
Для получения эпюр плоскость p2 вращением вокруг оси (Ох) совмещается с плоскостью p1 (рис. 25,б). Теперь сформулируем инварианты плоскопараллельного перемещения относительно p2:
1) горизонтальная проекция фигуры перемещается по плоскости чертежа, оставаясь равной самой себе (ï А2В2 ïïï);
2) фронтальные проекции точек фигуры перемещаются по горизонтальным прямым, параллельным оси проекций ((А1)ïï(В1)ïï(Ох).
Зная инварианты и проекции фигуры в первоначальном положении можно построить ее проекцию в интересующем нас положении: сначала вычерчиваем новую горизонтальную проекцию фигуры без изменения, располагая ее в любом удобном месте; затем определяем новую фронтальную проекцию фигуры по линиям связи, учитывая второй инвариант.
Инварианты плоскопараллельного перемещения относительно p1:
1) фронтальная проекция фигуры перемещается по плоскости чертежа, оставаясь равной самой себе;
2) горизонтальные проекции точек фигуры перемещаются по горизонтальным прямым, параллельным оси (Ох).
Если недостаточно одного плоскопараллельного перемещения, то можно воспользоваться несколькими плоскопараллельными перемещениями, выполняя их последовательно.
Способ вращения вокруг проецирующей прямой
Этот способ является частным случаем предыдущего. При вращении фигуры вокруг прямой i, называемой осью вращения, все точки этой фигуры описывают окружности в плоскостях, перпендикулярных к оси i. Центры этих окружностей определяются как точки пересечения соответствующих плоскостей и прямой i. Если ось i расположена перпендикулярно к p1 или p2, то плоскости окружностей, описываемых точками фигуры, будут параллельными p1 или p2. Поэтому указанные окружности проецируются на соответствующую плоскость проекций в окружности с сохранением натуральных величин.
Инварианты способа вращения вокруг проецирующей прямой:
1) проекции точек фигуры, на плоскость к которой перпендикулярна ось вращения, описывают концентрические окружности с центрами вырожденной в точку проекции оси вращения; при этом величина и форма этой проекции не изменяется;
2) другие проекции точек фигуры перемещаются по прямым, параллельным оси (Ох).
Пример. Построить натуральную величину угла между плоскостями a (АВС) и b (АВD) (рис.26).

Решение. Плоскости a и b образуют двугранный угол с ребром (АВ). Двугранный угол измеряется линейным углом, получаемым в пересечении его с плоскостью перпендикулярной к ребру. Поэтому следует решить сначала первую, а затем вторую задачу для ребра (АВ). После решения первой основной задачи (АВ) станет прямой уровня(), а после решения второй основной задачи – проецирующей прямой (). На рис. 26 первая ось i вращения проходит через точку В (В Î i ^ p1), а вторая ось j – через точку (Î j ^ p2). g ° ab – искомый угол.
Вращение вокруг прямой уровня.
Как было отмечено выше, окружности, описываемые точками фигуры при вращении, располагаются в параллельных плоскостях, перпендикулярных к оси вращения. Если осью вращения является фронталь, то точки фигуры остаются при вращении в фронтально проецирующих плоскостях, а если осью вращения является горизонталь, то – в горизонтально проецирующих плоскостях. Этот способ на практике применяется для определения натуральной величины плоской фигур, вращая ее до уровня соответствующей плоскости проекций. Поэтому его называют еще способом совмещения. Инварианты:
1) новая и старая проекции любой точки фигуры располагаются на одной прямой, перпендикулярной оси вращения;
2) длина новой проекции любого отрезка фигуры будет равна натуральной длине этого отрезка.
Строят только одну проекцию фигуры на ту плоскость проекций, на которую параллельна ось вращения. Между новой и старой проекциями фигуры устанавливается родство.
Вспомогательное проецирование
Построение новых проекций можно осуществить вспомогательным центральным параллельным проецированием заранее выбранную плоскость проекций. Плоскость проекций и центр или направление проецирования выбирают в зависимости от условий поставленной задачи.
Пример 2. Построить проекции точек пересечения прямой l(l 1,l 2) с поверхностью пирамиды SABCD.
Решение. Отметим произвольные точки 1 Îl и 2 Îl, а затем спроецируем из точки s на горизонтальную плоскость проекций пирамиду и прямую l. Пирамида проецируется в четырехугольник А2В2С2D2, а прямая l – в прямую 3242. Четырехугольник А2В2С2D2 и прямая 3242 пересекаются в двух точках 52 и 62. Последние две точки из центра s2 проецируются на прямую l 2 в точки К2 и L2, которые являются горизонтальными проекциями искомых точек пересечения К и L. Проведя через точки К2 и L2 линии связи, определяют проекции К1 Îl 1, L1 Îl 1 этих точек.
Основная литература: 1.7.1(38…..56, 62…102)
Дополнительная литература: 1.7.17 (30…40, 49…62), 1.7.10 (116…189),
1.7.11(62…80).
Контрольные вопросы.
1. Что такое «первая позиционная задача начертательной геометрии»? Что такое вторая?
2. Каким методом определяют видимость элементов фигур на эпюре?
3. Сформулируйте условие параллельности и условие перпендикулярности двух плоскостей.
4. Какие вы знаете свойства плоских углов? Теорема о прямом угле, что это такое?
5. Какие параметры определяют «методом прямоугольного треугольника»?
7. Определите расстояние от точки до прямой и плоскости общего положения.
8. В чем разница между методом плоскопараллельного переноса и методом вращения вокруг проецирующей прямой?
9. Как определяются натуральные величины плоских фигур методом замены плоскостей проекции и методом вращения вокруг линии уровня?
10. В чем особенность метода совмещения?

|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 593; Нарушение авторских прав?; Мы поможем в написании вашей работы!