
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Принцип компактности
|
|
|
|
Ранее было доказано, что всякая сходящаяся последовательность ограничена, обратное утверждение не верно. Однако следующая теорема дает возможность из ограниченной последовательности выделить сходящуюся подпоследовательность.
ТЕОРЕМА 3.16 (Больцано-Вейерштрасса). Всякая ограниченная последовательность содержит в себе сходящуюся подпоследовательность.
Доказательство. Так как по условию последовательность  ограничена, то существует отрезок
ограничена, то существует отрезок 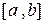 такой, что все элементы
такой, что все элементы  содержатся в этом отрезке:
содержатся в этом отрезке:  .
.
Разделим 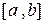 пополам:
пополам: 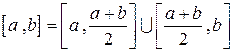 . Так как в последовательности
. Так как в последовательности  бесконечно много элементов (которые отличаются друг от друга, по крайней мере, порядковым номером), то одна из половинок
бесконечно много элементов (которые отличаются друг от друга, по крайней мере, порядковым номером), то одна из половинок 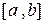 содержит бесконечное множество элементов последовательности
содержит бесконечное множество элементов последовательности  . Эту половину обозначим
. Эту половину обозначим 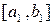 и отметим в ней из
и отметим в ней из  некоторый элемент
некоторый элемент  . Далее
. Далее 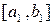 разделим пополам и выберем ту половину, которая содержит бесконечно много элементов
разделим пополам и выберем ту половину, которая содержит бесконечно много элементов  . Обозначим её
. Обозначим её 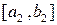 и отметим в ней элемент
и отметим в ней элемент 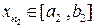 с номером
с номером  .
.
Продолжая этот процесс, получим последовательность вложенных отрезков 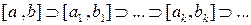 . Причем
. Причем 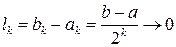 при
при 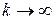 и
и 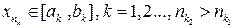 при
при 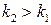 .
.
По построению 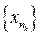 — подпоследовательность последовательности
— подпоследовательность последовательности  . Покажем, что эта подпоследовательность сходится. По принципу Кантора вложенных отрезков существует единственная точка
. Покажем, что эта подпоследовательность сходится. По принципу Кантора вложенных отрезков существует единственная точка 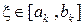 такая, что
такая, что
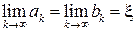 .
.
Таким образом, по теореме 3.6 доказано, что 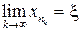 , то есть подпоследовательность
, то есть подпоследовательность 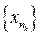 сходится.
сходится. 
Замечание 3.9. Теорему 3.16 часто называют принципом компактности.
Следствие 3.3. Всякое бесконечное ограниченное числовое множество  содержит в себе сходящуюся последовательность, все члены которой различны.
содержит в себе сходящуюся последовательность, все члены которой различны.
Доказательство. Возьмём произвольное число 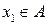 . Множество
. Множество 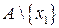 бесконечно, поэтому можем выбрать
бесконечно, поэтому можем выбрать 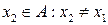 . Продолжая этот процесс неограниченно, мы выделим из
. Продолжая этот процесс неограниченно, мы выделим из  ограниченную последовательность (так как
ограниченную последовательность (так как  — ограничено)
— ограничено) 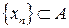 , все члены которой различны по построению.
, все члены которой различны по построению.
Применяя теорему Больцано-Вейерштрасса, из последовательности  выделим искомую сходящуюся подпоследовательность
выделим искомую сходящуюся подпоследовательность 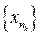 .
. 
Следствие 3.4. Из любой неограниченной последовательности можно выделить бесконечно большую подпоследовательность, которая имеет своим пределом бесконечность определённого знака.
Доказательство. Пусть последовательность  не ограничена сверху. Тогда существует номер
не ограничена сверху. Тогда существует номер 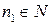 такой, что
такой, что 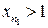 . Очевидно, что последовательность
. Очевидно, что последовательность 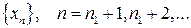 также не ограничена сверху (из исходной последовательности
также не ограничена сверху (из исходной последовательности  она получена отбрасыванием конечного числа первых членов). Поэтому существует номер
она получена отбрасыванием конечного числа первых членов). Поэтому существует номер 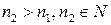 такой, что
такой, что 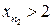 .
.
Продолжая процесс таким же образом, получим последовательность таких номеров 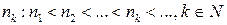 , что
, что 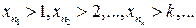 . Отсюда следует, что
. Отсюда следует, что 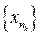 — подпоследовательность последовательности
— подпоследовательность последовательности  и
и 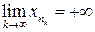 по построению.
по построению.
Аналогично доказывается для неограниченной снизу и неограниченной последовательностей. 
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 1912; Нарушение авторских прав?; Мы поможем в написании вашей работы!