Аналіз ДММБ

,

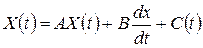де 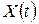— вектор обсягів валового випуску продукції по галузях у момент часу ;

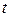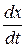— вектор абсолютних приростів за малу одиницю часу;

— матриця коефіцієнтів прямих витрат, включаючи витрати на заміщення вибуття основних фондів;

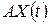— виробниче споживання, що забезпечує просте відтворення;

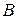— матриця коефіцієнтів капіталоємності приростів виробництва;

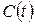— вектор-стовпчик, який характеризує споживання по галузях.

Виконуються такі умови:

1) матриця продуктивна і нерозкладна;

2) матриця коефіцієнтів повних витрат строго додатна: , ;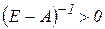

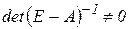3) капіталовкладення є єдиним джерелом зростання виробництва. У рамках даної моделі змістовно інтерпретуються лише ті траєкторії, для котрих виконується умова 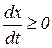. Такі стани системи та відповідні траєкторії в рамках ДММБ називаються допустимими.

Використаємо взаємозв¢язок між валовим суспільним продуктом (ВСП) і національним доходом (НД)

,

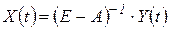вектор 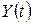характеризує галузеву структуру НД, отримаємо рівняння моделі Леонтьєва відносно НД

.

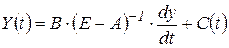(4)

Позначимо 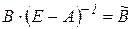. Коефіцієнт даної матриці 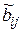характеризує величину виробничого накопичення продукції -го виду на одиницю приросту 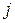-го елемента. НД, 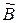— матриця коефіцієнтів повного приросту капіталоємності.

Для вивчення можливостей системи дослідимо модель (4) при різних траєкторіях споживання.

Установимо технологічні можливості системи, які визначаються параметрами і 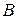. Для цього вважатимемо 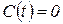. Тоді система (4)

.

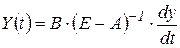Загальний розв¢язок має вигляд

,

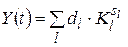(5)

де 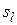— власні числа матриці повного приросту капіталоємності;

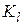— відповідні їм власні вектори;

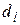— коефіцієнти, що визначаються з початкової умови .

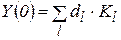Траєкторія, яка виходить із 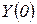, являє собою комбінацію експонент із різними темпами приросту 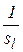. Отже, у загальному випадку розвиток по траєкторії 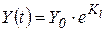, тобто з єдиним для всіх галузей темпом, неможливий, а відбувається з постійними структурними змінами.

Однак унаслідок припущення моделі матриця 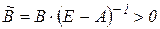, а значить у ній існує корінь Фробеніуса-Перрона 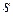. Величина кореня знаходиться у межах: .

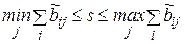Величина 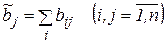називається повним приростом капіталоємності 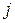-ї галузі.

Можливі два випадки поведінки траєкторії (5). У першому домінує експонента з показником степеня, який пов¢язаний із коренем Фробеніуса-Перрона. У цьому випадку із часом темп приросту кожного елемента НД починає наближатися до темпу, що визначається даною експонентою, тобто 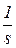. Таким чином, технологічний темп приросту 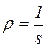. Структура НД прямує до власного вектора 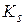. У другому випадку домінує експонента з показником степеня, відмінним від 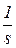. Це відбувається в умовах, коли існує додатне власне число, відмінне від 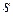. Нехай домінуючий показник 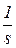. У даному випадку власний вектор обов¢язково має від¢ємні компоненти і, оскільки 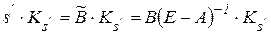, стовпчик 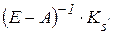, також містить від¢ємні компоненти. Ураховуючи (4), запишемо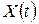

.

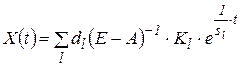У правій частині даної рівності наявні від¢ємні компоненти, зі зростанням 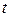вони збільшуються за абсолютною величиною. Відповідно зі збільшенням 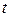вони з¢являються й у лівій частині рівності. Таким чином, траєкторія виходить у недопустиму область.

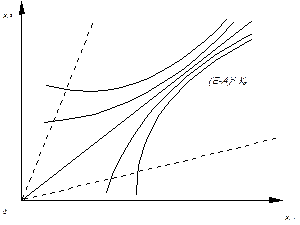
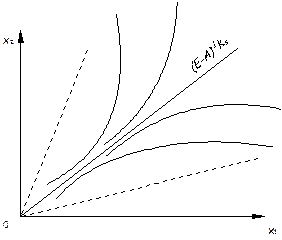
Рис. 6.1. Два випадки поведінки траєкторії

Траєкторії у першому випадку є допустимими, хоча початковий стан системи може бути й недопустимим.

У другому випадку початковий стан системи є допустимим, хоча траєкторія розвитку виходить за межі допустимої області.

Дата добавления: 2014-12-08