
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
III. Закрепление изученного материала. Скалярное произведение в координатах
|
|
|
|
Скалярное произведение в координатах
II. Изучение нового материала.
1. Скалярное произведение двух векторов можно вычислить, зная координаты этих векторов.
2. Изучение теоремы о скалярном произведении векторов в координатах и свойств скалярного произведения полезно построить так, чтобы учащиеся сами проводили алгебраические преобразования.
Полученные результаты можно записать в тетради и вынести в настенную таблицу:
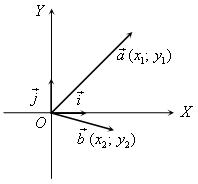
| 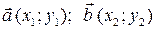
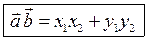
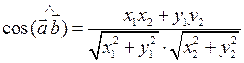
|
Свойства скалярного произведения векторов:
1) 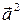 ≥ 0 (
≥ 0 (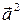 > 0 при
> 0 при 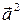
 0); 2)
0); 2) 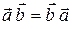 ;
;
3) 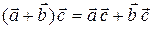 ; 4)
; 4) 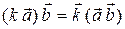 .
.
1. Решить задачу № 1043 (объясняет учитель):
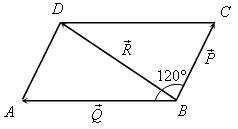
| Дано: 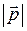 = 8; = 8; 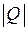 = 15; = 15;
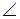 АВС = 120°.
Найти: АВС = 120°.
Найти: 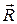 .
Решение
Пусть .
Решение
Пусть 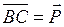 ; ; 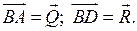
|
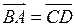 , тогда по правилу треугольника
, тогда по правилу треугольника 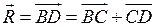 (или по правилу параллелограмма вектор
(или по правилу параллелограмма вектор 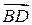 есть равнодействующая сила
есть равнодействующая сила 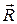 ).
).
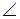 C = 180° – 120° = 60° (сумма односторонних углов равна 180°). По теореме косинусов из треугольника ВСD найдем ВD:
C = 180° – 120° = 60° (сумма односторонних углов равна 180°). По теореме косинусов из треугольника ВСD найдем ВD:
BD 2 = BC 2 + CD 2 – 2 BC ∙ CD ∙ cos C =
= 82 + 152 – 2 ∙ 8 ∙ 15 ∙ 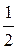 = 64 + 225 – 120 = 169;
= 64 + 225 – 120 = 169;
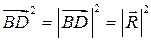 = 169;
= 169; 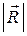 = 13.
= 13.
Ответ: 13.
2. Решить задачи № 1044 (а, б).
3. Устно № 1045.
4. Решить задачи № 1046, 1047 (б, в) на доске и в тетрадях.
5. Решить задачу № 1051.
Решение
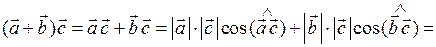
= 1 ∙ 2 cos 60° + 2 ∙ 2 cos 60° = 2 ∙ 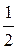 + 4 ∙
+ 4 ∙ 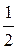 = 1 + 2 = 3.
= 1 + 2 = 3.
Ответ: 3.
6. Решить задачу № 1049 на доске и в тетрадях (для угла А объясняет учитель):
Решение
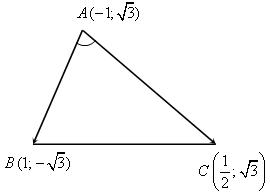
| 1) cos A = 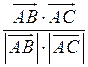
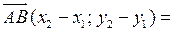
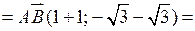
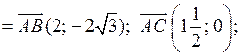
|
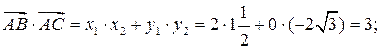
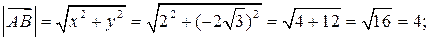
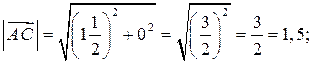
cos A = 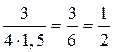 ; cos A =
; cos A = 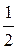 , то
, то 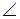 A = 60°.
A = 60°.
2) cos B = 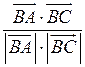 ;
; 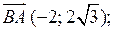
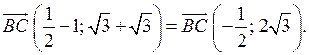
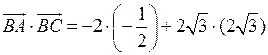 = 1 + 12 = 13;
= 1 + 12 = 13;
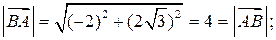
BC = 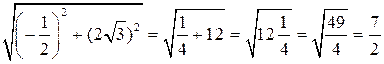 = 3,5;
= 3,5;
cos B = 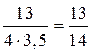 ≈ 0,9286;
≈ 0,9286; 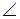 B находим по таблицам Брадиса:
B находим по таблицам Брадиса:
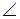 B ≈ 21°47′.
B ≈ 21°47′.
3) 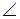 C = 180° – 60° – 21°47′ ≈ 98°13′.
C = 180° – 60° – 21°47′ ≈ 98°13′.
Ответ: 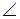 A = 60°;
A = 60°; 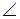 B ≈ 21°47′;
B ≈ 21°47′; 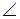 C ≈ 98°13′.
C ≈ 98°13′.
7. Решить задачу № 1052.
Решение
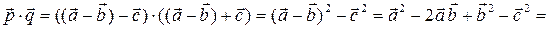
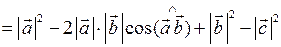 = 52 – 2 ∙ 5 ∙ 2 cos 90° + 22 – 42 =
= 52 – 2 ∙ 5 ∙ 2 cos 90° + 22 – 42 =
= 25 + 4 – 16 = 13; 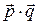 = 13.
= 13.
Ответ: 13.
8. Решить задачу № 1066.
Решение
По условию 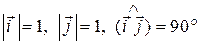 .
.
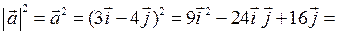
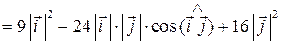 = 9 ∙ 1 – 24 ∙ 1∙ 1 ∙ 0 + 16 ∙ 1 = 25.
= 9 ∙ 1 – 24 ∙ 1∙ 1 ∙ 0 + 16 ∙ 1 = 25.
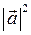 = 25, тогда
= 25, тогда 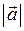 = 5.
= 5.
Ответ: 5.
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 501; Нарушение авторских прав?; Мы поможем в написании вашей работы!