Треугольник

Решение задач

IV. Итоги урока.

Домашнее задание: изучить материал пункта 127, ответить на вопросы 23–26, записать в тетради решение задач №№ 1224, 1225 (с. 333–335 учебника).

Об аксиомах и планиметрии (2 часа)

При завершении курса планиметрии в конце 9 класса два урока отводятся на ознакомление учащихся с аксиоматическим методом, в частности с системой аксиом, которые положены в основу изученного курса геометрии.

На первом уроке желательно провести с учащимися беседу об аксиоматическом методе в геометрии. В связи с этим необходимо напомнить им некоторые факты о возникновении и развитии геометрии. Для этой беседы рекомендуется использовать приложения 1 и 3 учебника: «Об аксиомах планиметрии» и «Некоторые сведения о развитии геометрии», а также дополнительную литературу.

В зависимости от уровня подготовки класса на втором уроке можно разобрать один или два примера теорем, которые в курсе были доказаны на основе наглядных представлений, и доказать их с использованием принятых в учебнике аксиом. Один из таких примеров (теорема, выражающая первый признак равенства треугольников) разобран в приложении 1 учебника.

при повторении курса геометрии необходимо сконцентрировать внимание учащихся на узловых вопросах программы.

Основные факты планиметрии и применяемые в ней методы можно сгруппировать по следующим темам:

1. «Треугольник» (2 часа).

2. «Окружность» (2 часа).

3. «Четырехугольники, многоугольники» (2 часа).

4. «Векторы, метод координат, движения» (2 часа).

Рассмотрение этих вопросов может включать обобщение и систематизацию сведений об основных свойствах геометрических фигур, доказательство отдельных теорем, решение комплексных задач.

При повторении полезно обращать внимание учащихся на различные методы геометрических доказательств. В зависимости от подготовки класса повторение можно проводить по всем или отдельным вопросам рассматриваемой темы.

Для организации итогового повторения можно воспользоваться подбором задач по указанным выше темам

Основные вопросы программы: равенство и подобие треугольников, сумма углов треугольника, равнобедренный треугольник, прямоугольный треугольник, площадь треугольника.

Задачи

1. В треугольниках АВС и DЕK АВ = DЕ, АС = DK, ВР = ЕМ, где Р и М – середины сторон АС и DK.

1) Докажите, что треугольник АВС равен треугольнику DЕK.

2) Найдите S_АВС, если ЕМ = 3 см, DK = 4 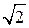см, 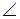ЕМK = 135°.

2. В треугольниках АВС и А ₁ В ₁ С ₁ АС = А ₁ С ₁, ВС = В ₁ С ₁, ВD = В ₁ D ₁, где ВD и В ₁ D ₁ – высоты треугольников, причем точки D и D ₁ лежат на отрезках АС и А ₁ С ₁.

1) Докажите, что треугольник АВС равен треугольнику А ₁ В ₁ С ₁.

2) Найдите радиус окружности, описанной около треугольника В ₁ D ₁ С ₁, если известно, что ВD = 6 см, DС = 8 см.

3) Найдите угол А ₁ С ₁ В ₁, если ВD = 6 см, DС = 8 см.

3. На рисунке дан прямоугольный треугольник АВС с гипотенузой АВ, DЕ 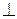АВ.

1) Докажите, что треугольник АВС и треугольник DАЕ подобны. 2) Найдите катеты треугольника АВС, если АВ = 13 см, АЕ = 5,2 см, DЕ = 2 см. 3) Докажите, что около четырехугольника ВDЕС можно описать окружность.

4. В прямоугольном треугольнике АВС проведена высота СD к гипотенузе АВ, СD = а, АD = b.

найдите: 1) ВС; 2) радиус окружности, вписанной в треугольник АВС; 3) отношение площадей треугольников АDС и АСВ.

5. В треугольнике АВС АВ = 14 см, АС = 15 см, ВС = 13 см.

найдите: 1) длину меньшей высоты треугольника; 2) площадь треугольника АDС, если АD – биссектриса треугольника АВС; 3) медиану АЕ треугольника АВС.

6. С помощью циркуля и линейки постройте треугольник АВС по сторонам АВ и АС и высоте, проведенной к АС.

7. Площадь треугольника АВС равна Q. Найдите площадь треугольника АОВ ₁, где О – точка пересечения медиан треугольника АВС, а В ₁ – середина стороны АС.

8. С помощью циркуля и линейки постройте равнобедренный треугольник АВС по основанию АС и углу В и биссектрису ВD внешнего угла этого треугольника при вершине В.

Дата добавления: 2014-12-08