Экспоненциальное сглаживание

Для экспоненциального сглаживания ряда используется рекур­рентная формула:

, (5.48)

где S_t - значение экспоненциальной средней в момент t;

a - параметр сглаживания, a = const, 0< a <l;

b = 1 - a.

Если последовательно использовать соотношение (5.48), то экспоненциальную среднюю S_t можно выразить через предше­ствующие значения уровней временного ряда. При

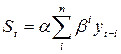. (5.49)

Таким образом, величина S_t оказывается взвешенной суммой всех членов ряда. Причем веса отдельных уровней ряда убывают по мере их удаления в прошлое соответственно экспоненциальной функ­ции (в зависимости от «возраста» наблюдений). Именно поэтому вели­чина названа экспоненциальной средней.

Например, пусть a =0,3. Тогда вес текущего наблюдения y_t будет равен a =0,3, вес предыдущего уровня у_t-1 будет соответствовать a x b =0,3x0,7=0,21; для уровня y_t-2 вес составит a х b² =0,147; для y_t-3 вес a х b³ =0,1029 и т.д.

Предположим, что модель временного ряда имеет вид:

y_t=a_t+e_t.

Английский математик Р. Браун показал, что математические ожидания ряда и экспоненциальной средней совпадут, но в то же вре­мя дисперсия экспоненциальной средней D [ S_t ] меньше дисперсии вре­менного ряда(s²)

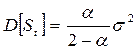. (5.50)

Из (5.50) видно, что при высоком значении a дисперсия экспоненциальной средней незначительно отличается от дисперсии ряда. С умень­шением a дисперсия экспоненциальной средней сокращается, возрастает ее отличие от дисперсии ряда. Тем самым, экспоненциальная средняя на­чинает играть роль «фильтра», поглощающего колебания временного ряда.

Таким образом, с одной стороны, следует увеличивать вес бо­лее свежих наблюдений, что может быть достигнуто повышением a (согласно (5.49)), с другой стороны, для сглаживания случайных откло­нений величину a нужно уменьшить. Эти два требования находятся в противоречии. Поиск компромиссного значения параметра сглажива­ния a составляет задачу оптимизации модели.

Иногда поиск этого значения параметра осуществляется путем перебора. В этом случае в качестве оптимального выбирается то значение a, при котором получена наименьшая дисперсия ошибки.

Экспоненциальное сглаживание является примером простейшей самообучающейся модели. Вычисления чрезвычайно просты, выпол­няются итеративно, причем массив прошлой информации уменьшен до единственного значения S_t-1.

Дата добавления: 2014-12-08