Примеры решения задач. Пример 1 Баллон вместимостью V = 5 л содержит смесь гелия и водорода при давлении P = 600 кПа

Пример 1 Баллон вместимостью V = 5 л содержит смесь гелия и водорода при давлении P = 600 кПа. Масса m смеси равна 4 г, массовая w₁ доля гелия равна 0,6. Определить температуру смеси, парциальные давления P₁ и P₂ , молярную массу смеси.

Решение.

Массовая доля w – отношение массы компонента смеси к массе смеси, т.е. . Аналогично, 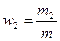. Следовательно, 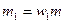и .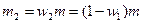

Найдем молярную массу смеси:

.

Здесь М₁ и М₂ – молярные массы компонентов смеси; М₁ = 4×10 ^-3 кг/моль, М₂ = 2×10 ^-3 кг/моль. Получаем:

.

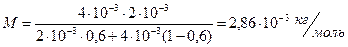Запишем уравнение Клапейрона – Менделеева для смеси:

.

Отсюда выразим и найдем температуру смеси:

.

Парциальное давление – давление, создаваемое компонентом смеси в сосуде. Таким образом, для нахождения можно использовать уравнение Клапейрона – Менделеева:

.

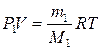Отсюда выразим и найдем парциальное давление Р₁:

.

Используя закон Дальтона Р = P₁ + P₂, находим P₂:

Р₂ = P - P₁ = 600 - 257,3 = 342,7 кПа.

Ответ: 258 К; 257,3 кПа; 342,7 кПа; 2,86×10^-3 кг/моль.

Пример 2 Определить кинетическую энергию вращательного движения одной молекулы кислорода при температуре Т = 286 К, а также кинетическую энергию 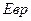вращательного движения всех молекул этого газа, если его масса равна 4 г.

Решение.

На каждую степень свободы молекул газа приходится одинаковая средняя энергия 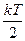, где k = 1,38×10^-23 Дж/К – постоянная Больцмана. Так как молекула кислорода двухатомная, то имеет 3 степени поступательного движения и 2 степени вращательного движения. Таким образом,

.

Кинетическая энергия вращательного движения всех молекул этого газа:

,

где N – число молекул газа, определяемое по формуле .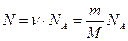

Таким образом, получаем

.

Ответ: 297Дж.

Пример 3 В центрифуге находится азот при температуре 17⁰С. Центрифуга, внутренний радиус которой 0,5 м, вращается вместе с азотом с частотой 80 с^-1. Во сколько раз давление в центре центрифуги меньше давления на расстоянии 0,4 м от оси вращения?

Решение.

Используем для решения распределение Больцмана в виде

,

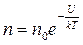где U – потенциальная энергия поля. Учтем, что вместо концентрации можем записать давление, так как 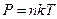и 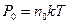. В этом случае получим

.

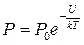На частицы газа в центрифуге действует центробежная сила инерции

.

Используем связь между потенциальной энергией и силой:

.

Тогда получим вид потенциального поля в центрифуге

.

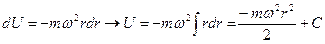Примем постоянную интегрирования С = 0. Тогда получим выражение для расчета давления газа в центрифуге:

.

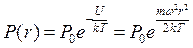Отсюда находим искомое отношение:

Учтем, что 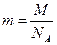- масса молекулы кислорода, 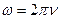- угловая скорость вращения, 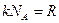- универсальная газовая постоянная.

В итоге получаем

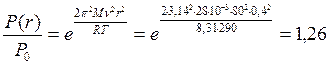
Ответ: в 1,26 раз.

Пример 4 Рассчитать среднее число столкновений, испытываемых за 5 с молекулой азота при температуре 17⁰С и давлении 10⁵ Па.

Решение.

Среднее число столкновений, испытываемых одной молекулой за единицу времени, равно

,

где d – эффективный диаметр молекулы; n - концентрация молекул; 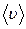- средняя арифметическая скорость теплового движения молекул.

За время t число столкновений составит

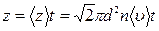(1)

Средняя арифметическая скорость определяется выражением

.

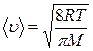Найдем концентрацию молекул:

.

Из уравнения Клапейрона - Менделеева выразим

.

Подставив полученные выражения в (1), получим:

.

.

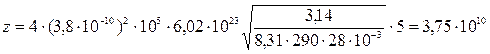Ответ: 3,75×10¹⁰.

Пример 5 Найти показатель адиабаты g для смеси газов, состоящей из количества n₁ = 5 моль гелия и количества n₂ = 3 моль азота.

Решение.

Показателем адиабаты g называется отношение удельных теплоемкостей смеси газа c_v (при постоянном объеме) и с_р (при постоянном давлении)

.

Удельную теплоемкость смеси газа c_v при постоянном объеме найдем из уравнения теплового баланса: количество теплоты, затраченное на нагрев смеси, равно количеству теплоты, идущему на нагрев компонент смеси, т.е.

.

Учтем, что 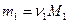, , , , 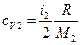а Dt одинаково, тогда получим

Отсюда выражаем c_v:

.

Гелий – одноатомный газ, поэтому у него число степеней свободы i₁ = 3, молярная масса гелия М₁ = 4×10^-3 кг/моль. Азот – двухатомный газ, поэтому у него число степеней свободы i₂ = 5, молярная масса азота М₂ = 28×10^-3 кг/моль.

Проводя аналогичные выкладки для расчета удельной теплоемкости смеси газа с_р при постоянном давлении, с учетом того, что 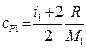и , получаем:

.

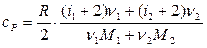Тогда показателем адиабаты g будет определяться выражением

.

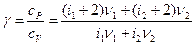Подставляя числовые значения, получим

.

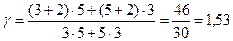Ответ: 1,53.

Пример 6 Кислород занимает объем V₁ = 1л и находится под давлением Р₁ = =200 кПа. Газ нагрели сначала при постоянном давлении до объема V₂ = 3л, а затем при постоянном объеме до давления Р₃ = 500 кПа. Найти: изменение DU внутренней энергии газа; совершенную им работу А; количество теплоты Q, переданное газу.

Решение.

Изменение внутренней энергии газа при его переходе из состояния 1 в состояние 3 найдем по формуле

Дата добавления: 2014-12-08