Показателей надёжности

Глава 1. Определение параметров планов испытаний

Для выбранного плана испытаний необходимо установить объём выборки N, который определяет точность и достоверность оценки оцениваемого параметра распределения или показателя надёжности.

Необходимый объём выборки для оценки средней наработки до отказа может быть определён по следующим формулам в случаях:

- экспоненциального распределения (b =1), распределения Вейбулла:

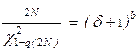(планы [NUN] и [NUz]); (1.1)

r=v*N (план [Nur]); (1.2)

- нормального распределения:

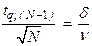(планы [NUN] и [NUz]); (1.3)

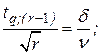r=v*N(план[Nur]); (1.4)

- логарифмически нормального распределения:

N= 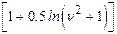. (план[NUN]) (1.5)

Здесь v – степень цензурирования;

t_q – квантиль распределения Стьюдента (табл. 4, прил. Б);

_q – квантиль нормального распределения (табл. 3, прил. Б);

n – коэффициент вариации;

d - относительная ошибка.

При выборе значений d, q и n можно пользоваться нижеследующими рекомендациями.

Рекомендации по выбору значений d и q

d q

Изделие в целом 0,15 - 0,20 0,80 - 0,90

Базовая деталь 0,10 - 0,15 0,90 - 0,95

Детали, обеспечивающие

безопасность изделия 0,05 0,95 - 0,99

Рекомендации по выбору значения коэффициента вариации n

Необходимость проведения капитального ремонта 0,3 - 0,6

Предельный износ 0,3 - 0,4

Разрушение:

- обусловленное сочетанием износа,

усталости, коррозии 0,3 - 0,4

- от усталости при изгибе, кручении 0,3 - 0,5

- крепёжных соединений 0,7 - 0,8

- от контактной усталости 0,6 - 0,7

Объём выборки при плане [NUN] может быть найден для:

- нормального распределения по графикам на рис. 1.1 и рис. 1.2;

- экспоненциального распределения по табл. 1.9;

- распределения Вейбулла по табл. 1.1 – 1.3;

- логарифмически нормального распределения по табл.1.8.

В случае экспоненциального распределения можно найти продолжительность испытаний по следующим зависимостям:

- при плане [NUT]:

Т=Т_ср..ln 1,781 N; (1.6)

- при плане [NUz]:

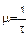; , (1.7)

где l– интенсивность отказов;

t– средняя наработка до цензурирования.

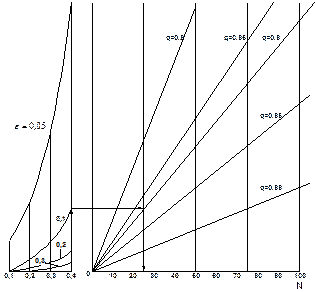
Рис.1.1. Номограмма по определению числа объектов испытания N при плане [NUN] и нормальном распределении для оценки среднего

Рис.1.2. Номограмма по определению числа объектов испытаний N при плане [NUN], нормальном распределении и ограниченном объеме совокупности М для оценки среднего

При плане [NUT] для заданного объёма выборки N определяется продолжительностью испытаний T из выражения:

T= Т_ср · , (1.8)

где - относительная продолжительность испытаний в долях средней наработки до отказа;

Т_ср – ориентировочное значение оцениваемой средней наработки до отказа.

Значения х определяют по формулам:

- для нормального распределения

; (1.9)

- для экспоненциального распределения (b =1) и распределения Вейбулла

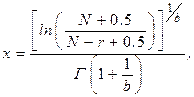(1.10)

где _v – квантиль нормального распределения уровня v;

N – заданный объём выборки;

r – прогнозируемое число отказов (предельных состояний), определяемое по рис. 1.1 и 1.2 и табл. 1.1 – 1.9;

b – параметр формы распределения Вейбулла;

- при плане [NMT]:

(1.11)

где r– прогнозируемое число отказов, определяемое по табл. 1.9.

Таблица 1.1

Число объектов испытаний N при плане [NUN]

и распределении Вейбулла при планировании

по предельной относительной ошибке

d	q	N при n
0,4	0,5	0,6	0,7	0,8	0,9	1,0
0,10	0,80
0,90
0,15	0,80
0,90
0,20	0,80
0,90

Таблица 1.2

Число объектов испытаний N при плане [NUN]

и распределении Вейбулла

при планировании по нижней доверительной границе

d	q	2.7	2.1	1.7	1.45	1.26	1.1
0,10	0,80
0,90
0,15	0,80
0,90
0,20	0,80
0,90

Таблица 1.3

Число объектов испытаний N при плане [NUN] и M = 10

для распределения Вейбулла

d	q	N при n
0.4	0.5	0.6	0.7	0.8	0.9	1.0
0,10	0,80
0,90
0,15	0,80
0,90
0,20	0,80
0,90

Таблица 1.4

Число объектов испытаний N при плане [NUN] и M = 20

для распределения Вейбулла

d	q	N при n
0.4	0.5	0.6	0.7	0.8	0.9	1.0
0,10	0,80
0,90
0,15	0,80
0,90
0,20	0,80
0,90

Таблица 1.5

Число объектов испытаний N при плане [NUN] и M = 30

для распределения Вейбулла.

d	q	N при n
0.4	0.5	0.6	0.7	0.8	0.9	1.0
0,10	0,80
0,90
0,15	0,80
0,90
0,20	0,80
0,90

Таблица 1.6

Число объектов испытаний N при плане [NUN] и M = 40

для распределения Вейбулла

d	q	N при n
0.4	0.5	0.6	0.7	0.8	0.9	1.0
0,10	0,80
0,90
0,15	0,80
0,90
0,20	0,80
	0,90

Таблица 1.7

Число объектов испытаний N при плане [NUN] и M = 50

для распределения Вейбулла

d	q	N при n
0.4	0.5	0.6	0.7	0.8	0.9	1.0
0,10	0,80
0,90
0,15	0,80
0,90
0,20	0,80
0,90

Таблица 1.8

Число объектов испытаний N при плане [NUN]

и логарифмически нормальном распределении

d	q	N при n
0.4	0.5	0.6	0.7	0.8	0.9	1.0
0,10	0,80
0,90
0,15	0,80
0,90
0,20	0,80
0,90

Таблица 1.9

Число отказов r в N испытаниях для планов [NMr] и [NMT]

d	r при q
0,50	0,80	0,90	0,95
0,05
0,10
0,15
0,20

Пример 1.1.

Определить необходимый объём выборки для комплекта вкладышей универсального шпинделя, чтобы с доверительной вероятностью q =0,9 ошибка при оценивании средней наработки до отказа не превышала d =0,1.

Решение.

Принята система технического обслуживания, при которой комплект вкладышей заменяется при достижении шарниром максимально допустимой величины износа. Следовательно, испытания шарнира шпинделя по определению средней наработки могут быть отнесены к плану [NUN] и допустимо предположение о принадлежности выборки по наработкам к нормальному распределению.

В соответствии с рекомендациями принимаем n=0,4 (предельный износ), а по графику (см.рис. 1.1) находим N =25.

Таким образом, для оценивания средней наработки до отказа с доверительной вероятностью q =0,9 и ошибкой d =0,1 необходимо иметь данные о наработках не менее 25 комплектов вкладышей.

Пример 1.2.

При плане [NUN] определить необходимый объём выборки для оценивания средней наработки до отказа шпинделя линии привода валков q =0,9; d =0,1. Известно, что выборка принадлежит распределению Вейбулла с коэффициентом вариации n=0,8. Предполагается, что общее число замен шпинделей за время эксплуатации линии привода валков не превысит 10 шт.

Решение.

Так как мы имеем ограниченный объём совокупности (10 шпинделей), то по табл. 3 находим N =7 шт.

Таким образом, произвести оценивание средней наработки на отказ шпинделя линии привода валков с доверительной вероятностью q =0,9 и ошибкой d =0,1 мы сможем, только имея данные о наработках до отказа 7 шпинделей.

Пример 1.3.

При плане [NUT] определить продолжительность испытаний карданного вала линии привода формирующего ролика моталки для оценивания средней наработки до отказа с доверительной вероятностью q =0,9 и ошибкой d =0,1. Предположительно выборка принадлежит к распределению Вейбулла с параметром b =2. Ориентировочное значение средней наработки до отказа Т _ср =25 сут.

Решение.

Из зависимости (1.8):

Т=Т_срЧх =25 х 0,617=17,4 сут.

По формуле (1.10) находим

Дата добавления: 2014-12-08