Распределение Вейбулла 2 страница

Если же о функции распределения ничего не известно (кроме её непрерывности) или известна её принадлежность к некоторому непараметрическому классу распределений (ВФИ-распределение), то используются непараметрические модели оценивания.

3.2. Непараметрические модели оценивания

В том случае, когда нет априорной информации о виде закона распределения ресурса, а объём имеющихся данных не позволяет достаточно обоснованно выбрать какое-либо параметрическое семейство распределений, используются непараметрические модели оценивания показателей долговечности.

Различают непараметрические модели оценивания общего вида, справедливые для произвольных функций распределения ресурса, и непараметрические модели частного вида, когда функция распределения ресурса принадлежит к ВФИ или ВСФИ-распределениям (см. гл. 4, 6 части I).

Анализ отказов металлургического оборудования показывает, что наработки до отказа (на отказ) деталей и узлов, как правило, описываются распределениями с возрастающей функцией интенсивности отказов (ВФИ - распределения). В этом случае точечные оценки среднего ресурса Т можно получить, используя следующие статистики:

– для плана [NUN]

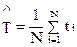, (3.1)

где t _i – i -й член вариационного ряда из наработок;

– для плана [NUz]

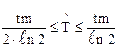, (3.2)

где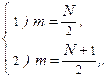

если: 1) N –чётное число; 2) N –нечётное число.

Нижняя доверительная граница (НДГ) оценки среднего ресурса для плана [NUN]:

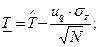(3.3)

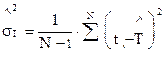; (3.4)

для плана в случае ВФИ-распределения

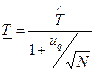. (3.5)

Пример 3.1.

По результатам наблюдений за работой карданного вала 4-го формирующего ролика моталки были зафиксированы следующие наработки, сут: 98, 85, 68, 40, 74, 90, 20, 19, 31, 26, 26, 24. Найти оценку среднего ресурса и его НДГ при q=0.9.

Решение.

Так как наблюдения проводились по плану [NUN], то воспользуемся зависимостями (3.1), (3.3), (3.4).

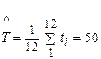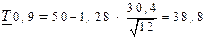сут.

сут.

_0,9=1,28 из табл. 3, прил. Б.

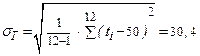сут.

3.3. Оценивание среднего ресурса

на основании информации о величине износа

В некоторых случаях, когда возможен контроль величины износа, появляется возможность прогнозировать величину среднего ресурса изделия, не дожидаясь появления отказа изделия.

Известно, что величину износа " U " можно описать функцией

U=U₀+I_t·t, (3.6) где U₀ - начальный зазор в паре трения,

I _t - скорость изнашивания.

Оценкой параметров U, U₀, I_t являются 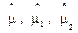соответственно, тогда

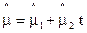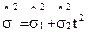, (3.7)

и точечная оценка среднего ресурса Т:

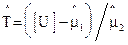, (3.8)

где [U] – предельно допустимая величина износа.

Нахождение оценок 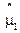и 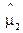будет зависеть от методики проведения измерений величины износа.

По первой методике замеры зазора в узле трения или размера изнашиваемой детали производятся для N объектов в начальный момент времени t= 0 и через заданный момент времени t=t₁.

По второй методике замеры зазора в узле трения или размеры изнашиваемой детали производятся для N объектов в начальный момент времени и через определённые заданные промежутки времени t₁, t₂ ј 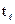, где 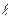– число замеров.

Вторая методика даёт более точные значения среднего ресурса, но существенно усложняются расчёты.

При использовании первой методики для получения точечной оценки среднего ресурса 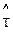значение 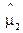(оценки математического ожидания скорости изнашивания) находят из зависимости (3.7).

Нижняя доверительная граница (НДГ) среднего ресурса 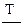находится из соотношения:

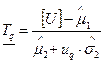, (3.9)

где 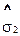- из зависимости (3.7).

Необходимо отметить, что соотношение (3.9) даёт несколько завышенные (но несущественные для условий эксплуатации металлургического оборудования) значения НДГ среднего ресурса, так как оно получено для условия неизменности начального зазора.

Более точные значения НДГ среднего ресурса можно получить при использовании второй методики, производя несколько замеров в заданные моменты времени, тогда:

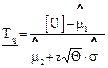, (3.10)

где ;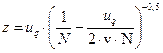

;

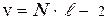N – число объектов, в которых производятся замеры;

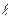– число замеров на одном объекте;

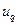– квантиль нормального распределения для доверительной вероятности q.

Точечные оценк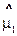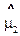и , и 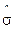определяются по методике, рассмотренной в прим. 3.3.

Точечная оценка гамма-процентной наработки 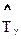находится из зависимости (3.10) для .

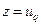НДГ гамма-процентной наработки 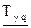находится также из зависимости (3.10) при

.

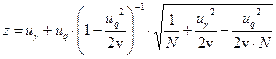Пример 3.2.

Измерения зазора в шарнире универсального шпинделя слябинга 1150 в начальный момент времени и через 20 суток на трёх комплектах вкладышей дали следующие результаты: [1,1 мм, 4,7 мм], [1,0 мм, 4,3 мм], [0,9 мм, 4,0 мм]. Найти точечную оценку среднего срока службы и его НДГ при доверительной вероятности q =0,9, если допустимая величина износа [U] =15 мм.

Решение:

Значение точечной оценки среднего срока службы находим из зависимости (3.8)

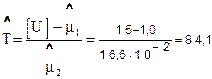
	сут.
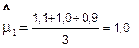
	мм.
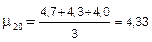
	мм.
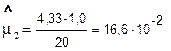
	мм/сут.

НДГ среднего срока службы по зависимости (3.9):

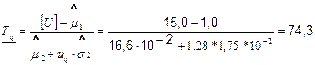сут.

;

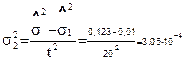s ₂ =1,75Ч10 ^-2.

;

;

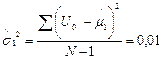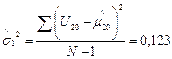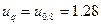(из табл. 3, прил. Б).

Пример 3.3.

Измерения зазора в шарнире универсального шпинделя в начальный момент времени, через 14, 28 сут на трёх комплектах вкладышей дали следующие результаты, мм: [1,1-2,7-4,3]; [1,0-2,5-4,3]; [0,9-2,3-4,0]. Найти значения показателей долговечности комплекта вкладышей 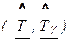. Известно, что отношение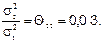

Решение.

В соответствии с зависимостью (3.10) необходимо найти оценки среднего зазора 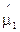; средней скорости изнашивания 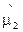и средне квадратичного отклонения измеряемого параметра (зазора) .

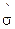Принимаем, что изменение зазора в шарнире описывается зависимостью

U(t)=U₀+I _t · t+e(t)

или

U(t)=U₀ ·j₁(t)+I _t ·j₂(t)+e(t),

где U₀ - начальный зазор;

I _t - скорость изнашивания;

j₁(t), j₂(t) - базисные функции;

e(t) - не зависящий от U₀ и I _t слабо коррелированный случайный шум, дисперсия которого удовлетворяет условию:

D²=D[e(t)]/D(U₀)= 0,01.

Случайный шум есть результат появления накапливающихся случайных ошибок при измерении величины износа, которые независимы и распределены нормально с нулевым средним значением и дисперсией вида s² ·D², где D² - заданная величина.

Полагаем, что U(t), U₀, I _t – нормально распределённые случайные величины с математическими ожиданиями s²; s₁²; s₂² соответственно. Тогда

m=m₁ + m₂t + e(t).

Измерения зазоров в шарнире производятся в регламентированные моменты времени t =0, 14 сут, 28 сут на трёх комплектах вкладышей.

Данные об измерении зазора в указанные моменты времени представим в виде трёх векторов 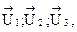компоненты которых есть измеренные значения реализаций процесса U(t) в эти моменты времени, мм.

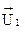= | 1,1; 2,7; 4,3 |^T,

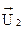= | 1,0; 2,5; 4,3 |^T,

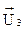= | 0,9; 2,3; 4,0 |^T.

В нашем случае число реализаций N =3, число измерений на каждой реализации l=3, а матрицы

,

.

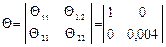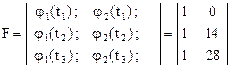Оценки 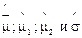определяются на основе обобщённого метода наименьших квадратов по формулам, использующим матричное умножение:

;

,

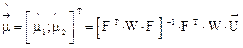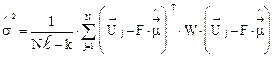где k - число неизвестных параметров (k =2);

W=(F·Q·F ^T +D² I _l ) ^{- 1} ;

I _l - единичная матрица порядка l;

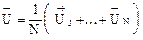- среднеарифметическое результатов измерений N реализаций.

Вычислим вспомогательные матрицы W и (F ^T ·W·F) ^{- 1} .

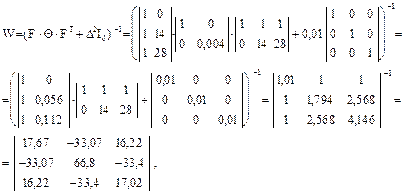
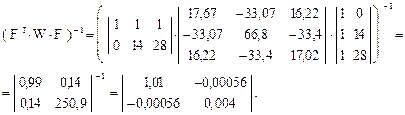
Вычислим матрицу

:

,

,

.

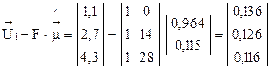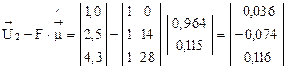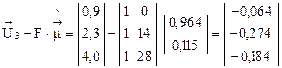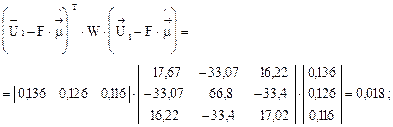
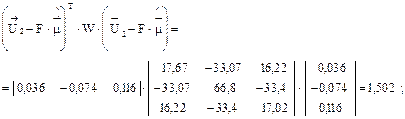
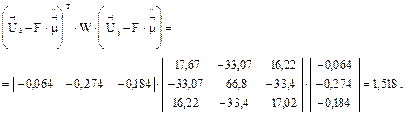
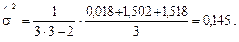
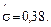
Находим среднюю наработку Т и её нижнюю доверительную границу (НДГ) .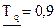

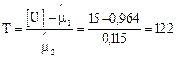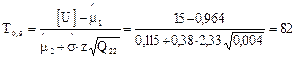сут.

сут.

.

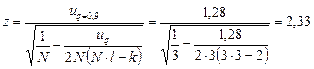3.4. Оценивание остаточного ресурса

В процессе эксплуатации металлургического оборудования осуществляются плановые замены деталей и узлов. Решение вопроса о замене того или другого узла в плановый ремонт может определяться величиной остаточного ресурса узла на данный момент времени.

Под остаточным (после времени t) ресурсом объекта понимается его наработка, начиная с момента t до перехода в предельное состояние при установленных режимах применения и условиях эксплуатации.

Одним из основных показателей остаточной долговечности является средний остаточный ресурс T(t), (математическое ожидание остаточного ресурса после времени t).

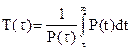, (3.11)

где R(t) – вероятность безотказной работы в момент времени t.

Точечная оценка остаточного ресурса находится из зависимости:

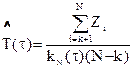, (3.12)

где Z _i = t _i -t;

t _i – наработка после времени t;

;

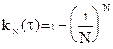k – число отказавших объектов на интервале [ 0, t ].

Нижняя доверительная граница (НДГ) остаточного ресурса уровня q определяется из зависимости:

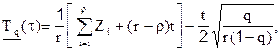(3.13)

где r и r – число объектов на интервале [t; t + t] соответственно наблюдаемых и отказавших;

t – продолжительность наблюдения после t.

Пример 3.4.

По наблюдениям за 23-мя карданными валами (план [NUN]) в линии привода формирующего ролика моталки были получены следующие наработки до предельного состояния, сут: 54, 36, 7, 21, 24, 77, 12, 14, 94, 10, 13, 77, 25, 21, 4, 10, 94, 63, 13, 3, 13, 4, 15. Найти точечную оценку остаточного ресурса и его НДГ после 20 суток.

Решение.

Находим точечную оценку остаточного ресурса .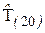

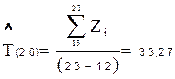
сут.

Z _i = t _i -20 = (34, 16, 1, 4, 57, 74, 57, 5, 1, 74, 43).

Находим нижнюю доверительную границу (НДГ) уровня q =0,8.

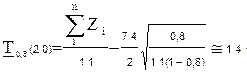
сут.

Приложение Б

ЗНАЧЕНИЯ ФУНКЦИЙ

И КВАНТИЛЕЙ РАСПРЕДЕЛЕНИЯ

Таблица 1

Значение нормированной функции Лапласа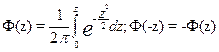

Z	Сотые доли z
0,0	0,00000	0,00399	0,00798	0,0119	0,01595	0,01994	0,0239	0,0279	0,0318	0,03586
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7

Окончание табл.1
Z	Сотые доли z
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9

z	Ф(z)	z	Ф(z)	z	Ф(z)	z	Ф(z)
3,0 3,1 3,2 3,3	0,49865 0,49903 0,49931 0,49952	3,4 3,5 3,6	0,49966 0,49977 0,49984	3,7 3,8 3,9	0,49989 0,49993 0,49995	4,0 4,5 5,0	0,499968 0,499997 0,49999997

Таблица 2

Значение ординат плотности нормированного нормального распределения -j(z)

Z	.00	.01	.02	.03	.04	.05	.06	.07	.08	.09
.0	.3989	.3989	.3989	.3988	.3986	.3984	.3982	.3980	.3977	.3973
.1	.3970	.3965	.3961	.3956	.3951	.3945	.3939	.3932	.3925	.3918
.2	.3910	.3902	.3894	.3885	.3876	.3867	.3857	.3847	.3836	.3825
.3	.3814	.3602	.3790	.3778	.3765	.3752	.3739	.3725	.3712	.3697
.4	.3683	.3668	.3653	.3637	.3621	.3605	.3589	.3572	.3555	.3538
.5	.3521	.3503	.3485	.3467	.3448	.3429	.3410	.3391	.3372	.3352
.6	.3332	.3312	.3292	.3271	.3251	.3230	.3209	.3187	.3166	.3144
.7	.3123	.3101	.3079	.3056	.3034	.3011	.2989	.2966	.2943	.2920
.8	.2897	.2874	.2850	.2827	.2803	.2780	.2756	.2732	.2709	.2685
.9	.2661	.2637	.2613	.2589	.2565	.2541	.2516	.2492	.2468	.2444
1.0	.2420	.2396	.2371	.2347	.2323	.2299	.2275	.2251	.2227	.2203
1.1	.2179	.2155	.2131	.2107	.2083	.2059	.2036	.2012	.1989	.1965
Окончание табл.2
Z	.00	.01	.02	.03	.04	.05	.06	.07	.08	.09
1.2	.1942	.1919	.1895	.1872	.1849	.1826	.1804	.1781	.1758	.1736
1.3	.1714	.1691	.1669	.1647	.1626	.1604	.1582	.1561	.1539	.1518
1.4	.1497	.1476	.1456	.1435	.1415	.1394	.1374	.1354	.1334	.1315
1.5	.1295	.1276	.1257	.1238	.1219	.1200	.1182	.1163	.1145	.1127
1.6	.1109	.1092	.1074	.1057	.1040	.1023	.1006	.0989	.0973	.0957
1.7	.0940	.0925	.0909	.0893	.0878	.0863	.0848	.0833	.0818	.0804
1.8	.0790	.0775	.0761	.0748	.0734	.0721	.0707	.0694	.0681	.0669
1.9	.0656	.0644	.0632	.0620	.0608	.0600	.0584	.0573	.0562	.0551
2.0	.0540	.0529	.0519	.0508	.0498	.0488	.0478	.0468	.0459	.0449
2.1	.0440	.0431	.0422	.0413	.0404	.0396	.0387	.0379	.0371	.0363
2.2	.0355	.0347	.0339	.0332	.0325	.0317	.031O	.0303	.0296	.0290
2.3	.0283	.0277	.0270	.0264	.0258	.0252	.0276	.0241	.0235	.0229
2.4	.0224	.0219	.0213	.0208	.0203	.0198	.0194	.0189	.0184	.0180

Таблица 3

Дата добавления: 2014-12-08