Экспоненциальное распределение

.

Принимаем N =50 шт. в предположении, что такое количество замен будет произведено в течение трёх лет. Тогда по табл. 7 находим r= 16.

Но так как на испытания ставятся не все 50 карданных валов одновременно, а последовательно один за другим, то общая продолжительность испытания составит

T _S =17,4 х 50= 870 суток или 2,4 года.

Если же осуществить оценивание с доверительной вероятностью q =0,8 и ошибкой d =0,2, то r =8 и

Т=25 х 0,469=11,7 сут.,

а общая продолжительность испытаний составит

T _S =11,7 х 50=586 (сут)» 1,6 года.

Глава 2. Оценивание показателей безотказности

2.1. Оценивание показателей безотказности на основе

параметрических методов

Когда известен вид закона распределения наработки до отказа, то точечное и интервальное оценивание показателей безотказности осуществляется по нижеприведенным формулам в зависимости от вида распределения.

Точечное оценивание:

– средняя наработка

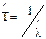, ( 2.1)

где - точечная оценка параметра экспоненциального распределения;

– интенсивность отказов

; (2.2)

– гамма-процентная наработка

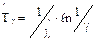; (2.3)

– вероятность безотказной работы

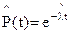. (2.4)

Определение нижней доверительной границы (НДГ) средней наработки и гамма-процентной наработки при плане [NUN]:

; (2.5)

; (2.6)

при плане [NUT] N=r;

при плане [NUz] (N –1)= N.

Пример 2.1.

При проведении исследований на надёжность карданного вала формирующего ролика моталки были получены следующие значения наработок в сутках: 1, 4, 26, 5, 15, 5, 8, 3, 12, 5. Найти точечные и интервальные оценки показателей безотказности в случае экспоненциального распределения.

Решение:

Используя формулы (2.1) и (2.3), найдем точечные оценки для:

– средней наработки до отказа

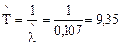сут;

– гамма-процентной наработки для g =0,8

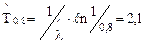сут;

Используя формулы (2.5), (2.6), найдём НДГ для:

– средней наработки до отказа для q =0,8

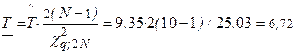сут.;

значение квантили 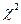_q;N находим из табл. 5, прил. Б;

– гамма-процентной наработки для (g =0,8, q =0,8)

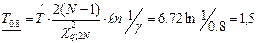сут.

То есть истинное значение средней наработки до отказа при доверительной вероятности q =0,8 не ниже 6,72 сут.

И если мы хотим обеспечить безопасную работу с вероятностью g =0,8, то необходимо осуществлять замену карданного вала через 1,5 сут либо иметь к этому моменту времени карданный вал, готовый к замене.

С другой стороны, такие значения показателей безотказности характеризуют крайне низкий уровень надёжности и требуется разработка технических решений по увеличению средней наработки до отказа.

Дата добавления: 2014-12-08