Распределение Вейбулла 1 страница

Логарифмически нормальное распределение

Точечное оценивание:

– средняя наработка

; (2.13)

– гамма-процентная наработка

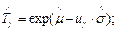(2.14)

– интенсивность отказов

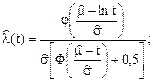(2.15)

– вероятность безотказной работы

+0,5. (2.16)

Находятся значение квантили u_g из табл. 3, прил. Б; функция j(z) из табл. 2, прил. Б; функция F(z) из табл. 1, прил. Б.

Определение нижней доверительной границы (НДГ) средней наработки до отказа и гамма-процентной наработки при плане [NUN]:

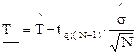; (2.17)

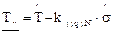, (2.18)

где t_{q; (N–1)} - квантиль распределения Стьюдента (табл. 4, прил. Б);

k_{g; q; N} - коэффициент, значения которого приведены в табл. 9, прил. Б;

при плане [NUT] N=r;

при плане [NUz] .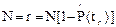

Точечное оценивание:

– средняя наработка

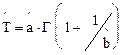; (2.19)

– гамма-процентная наработка

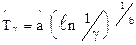; (2.20)

– интенсивность отказов

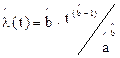; (2.21)

– вероятность безотказной работы

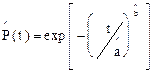, (2.22)

где - оценки параметров распределения Вейбулла.

Значения Г(х) берут из табл. 6,прил. Б.

Определение нижней доверительной границы (НДГ) средней наработки до отказа и гамма-процентной наработки при планах [NUN], [NUT]:

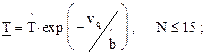(2.23)

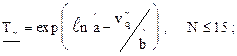(2.24)

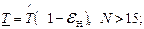(2.25)

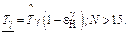(2.26)

где v_q, v^g_q - квантили распределения V - статистики, определяемой из табл. 8, прил. Б. При определении значений v_q, v^g_q для плана [NUz] следует полагать, что ;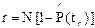

e_H=¦( n ,q,N) - определяется из табл. 10, 11, прил. Б;

n - коэффициент вариации для распределения Вейбулла, определяемый по зависимости:

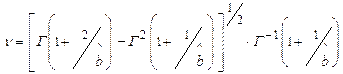(2.27)

.

Пример 2.3.

При испытаниях на надёжность 12-й секции транспортного рольганга была получена выборка по наработкам в сутках, которая после упорядочения приняла следующий вид: 24, 30*, 42, 48, 60*, 70, 75, 78, 84, 90*, 90*, и после статистической обработки были получены оценки параметров распределения Вейбулла 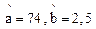. Звёздочкой отмечены наработки до цензурирования. Найти точечные и интервальные оценки показателей безотказности секции транспортного рольганга.

Решение.

Находим точечные оценки по формулам (2.19)-(2.22):

– средняя наработка до отказа

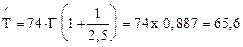сут;

– гамма-процентная наработка для g =0,9

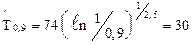сут;

– интенсивность отказов для t =50 сут

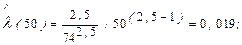
– вероятность безотказной работы

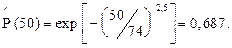
Находим НДГ средней наработки до отказа и гамма-процентной наработки по формулам (2.23), (2.24) для q =0,9, g =0,9.

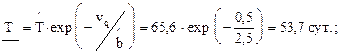
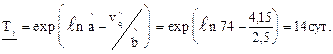
Для нахождения квантили v_q и v^g_q по табл. 8, прил. Б при плане [NUz] необходимо найти значения r и P(t_r) по формулам (2.28), (2.29).

;

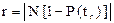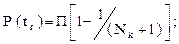
Р(24)=[1-1/(10+1)]=0,909;

P(42)=0,909 x [1-1/(8+1)]=0,808;

P(48)=0,808 x [1-1/(7+1)]=0,707;

P(70)=0,707 x [1-1/(5+1)]=0,589;

P(75)=0,589 x [1-1/(4+1)]=0,471;

P(78)=0,471 x [1-1/(3+1)]=0,353;

P(84)=0,353 x [1-1/(2+1)]=0,235;

r =| 11 x (1-0,235) |=| 8,4|=8.

Тогда

Пример 2.4.

При испытаниях по плану [NUz] на надёжность подшипника скольжения в механизме уравновешивания нижнего шпинделя линии привода валков была получена выборка по наработкам на отказ в сутках, которая после упорядочения приняла следующий вид: 3, 5, 8, 9, 11, 15, 18, 21, 23, 24, 30*, 30*, 30*, 36, 41, 46, 56, 58, 70, 82. Звёздочкой отмечены наработки до цензурирования. Известно, что наработки описываются распределением Вейбулла с параметрами 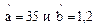. Установить точечные и интервальные оценки показателей безотказности подшипника скольжения.

Решение.

Найдём точечные оценки по формулам (2.19), (2.20), (2.22).

средняя наработка до отказа

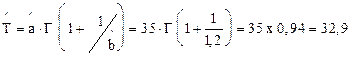сут;

значения Г(х) находят из табл. 6, прил. Б;

– гамма-процентная наработка для g =0,8

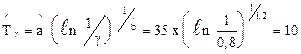сут;

– вероятность безотказной работы для t =20 сут

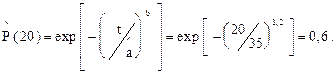
Найдём НДГ средней наработки до отказа и гамма-процентной наработки для g =0,8 при доверительной вероятности q =0,8 по формулам (2.25), (2.26), т.к. общее число наработок N =18.

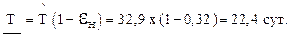
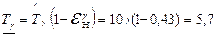сут.

Для нахождения e_H из табл. 10, прил. Б и e^g_H из табл. 11, прил. Б определён коэффициент вариации n по формуле (2.27).

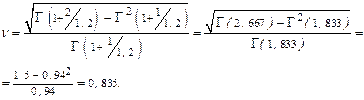
2.2. Оценивание показателей безотказности

на основе непараметрических методов

Оценку показателей безотказности можно получить и тогда, когда нам неизвестен вид закона распределения или известно, что распределение относится к классу возрастающей функции интенсивности отказов (ВФИ-распределение).

В этом случае оценивание осуществляют на основе непараметрических методов, одним из которых является метод множительной оценки показателей безотказности.

Начинают с вычисления функции распределения наработок непосредственно по упорядоченной статистической совокупности, в которой наработки до отказа и до цензурирования выстроены в порядке неубывания. Если значения наработки до цензурирования равны значениям наработки до отказа, то сначала указывается наработка до отказа, затем наработка до цензурирования.

Для каждой наработки до отказа t_i вычисляют оценки вероятности безотказной работы 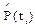и вероятность отказа .

Вычисления при планах [NUN], [NUT] производят по формулам:

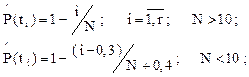(2.28)

при плане [NUz] по формуле

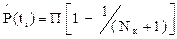, (2.29)

где N_к - число работоспособных изделий после отказа при наработке t_к;

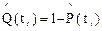. (2.30)

Точечное оценивание осуществляют по нижеследующим формулам:

– средняя наработка до отказа

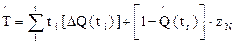, (2.31)

где 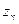=max(t_r, t_r) - наработка до отказа;

t_n - наработка до цензурирования;

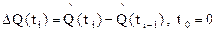; (2.32)

– гамма-процентная наработка

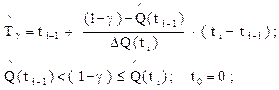(2.33)

– вероятность безотказной работы

(2.34)

Определение НДГ средней наработки до отказа осуществляется по формуле:

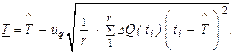(2.35)

Распределения с возрастающей функцией

интенсивности отказов (ВФИ- распределения )

Точечное оценивание средней наработки до отказа в случае ВФИ- распределения производят по приближённой формуле:

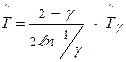, (2.36)

где 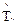- точечная оценка гамма-процентной наработки до отказа при 0,368< g Ј0,6;

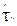- вычисляется по формуле (2.33).

Определение НДГ средней наработки до отказа осуществляется по формуле:

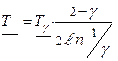; 0,368< g Ј0,6; (2.37)

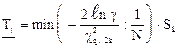, (2.38)

где к - наибольшее число, при котором

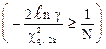; (2.39)

S_к - суммарная наработка до к -го отказа

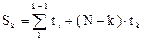. (2.40)

Пример 2.5.

Имеется упорядоченная статистическая совокупность по наработкам карданного вала формирующего ролика 4*, 5, 6*, 7, 8, 9, 9, 10, 10*, 12, 12, 12*, 15, 21 (звездочкой обозначены наработки до цензурирования). Найти точечные оценки вероятности безотказной работы для наработки t =9 сут, точечную и НДГ средней наработки до отказа для q =0,9.

Решение.

Найдём точечную оценку средней наработки до отказа по формулам (2.29) - (2.32).

Q(5)=1/13=0,077; Q(7)=2/12=0,167; Q(8)=3/12=0,25;

Q(9)=4/12=0,333; Q(9)=5/12=0,417; Q(10)=6/12=0,5;

Q(12)=7/11=0,636; Q(12)=8/11=0,729; Q(15)=9/10=0,9;

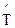=5 x (0,077-0)+7 x (0,167-0,077)+8 x (0,25-0,167)+9 x (0,333-0,25)+9 x (0,417-0,333)+10 x (0,5-0,417)+12 x (0,636-0,5)+12 x (0,729-0,636)+15 x (0,9-0,729)+21 x (1-0,9)=11,4 сут.

Нижнюю доверительную границу НДГ средней наработки найдём по формуле (2.35).

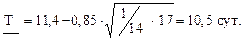
=0,077 х (5,4)²+0,09 х (- 4,4)²+0,038 х (-3,4)²+0,083 х (-2,4)²+0,084 х (-2,4)²+0,083 х (-1,4)²+0,136 х (0,6)²+0,093 х (0,6)²+0,171 х (3,6)²+0,1 х (9,6)²=17.

Найдём точечную оценку вероятности безотказной работы для наработки

t =7 сут и t =6 сут по формуле (2.29).

;

.

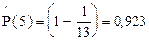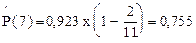По формуле (2.34) найдём

.

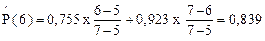Сравнивая полученные значения и 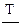с оценками, полученными в прим. 2.2, видим, что оценки средней наработки до отказа получаются несколько завышенными, а оценка вероятности безотказной работы - заниженной.

То есть отсутствие информации о законе распределения наработок до отказа снижает точность получаемых оценок.

Пример 2.6.

По условиям прим. 2.5, если известно, что мы имеем дело с ВФИ-распределением, найти точечные и НДГ оценки средней наработки до отказа и гамма-процентной наработки.

Решение.

Найдём точечную оценку средней наработки до отказа. Точечная оценка средней наработки до отказа находится по формулам (2.31), (2.33) и получена в прим. 2.5. В случае ВФИ- распределения можно воспользоваться формулами (2.36), (2.33).

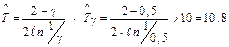сут.

Примем g =0,5, тогда Q(9)<1-0,5Ј Q(10) и

.

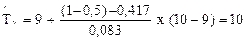Найдём точечную оценку гамма-процентной наработки g =0,8 по формулам (2.33):

.

Из прим. 2.5:

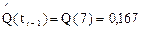, Q(t_i)= Q(8)=0,25;

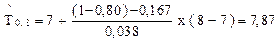сут.

НДГ средней наработки до отказа и гамма-процентной наработки находим по формулам (2.37) - (2.40).

Для вычисления 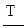полагаем g =0,5.

Вычислим 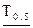при q =0,9:

при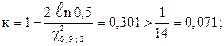

при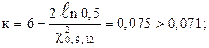

при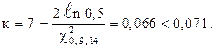

Поэтому выбираем к =6, тогда суммарная наработка по формуле (2.40)

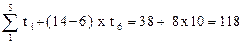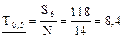сут.

сут.

Следовательно, НДГ средней наработки до отказа по формуле (2.37)

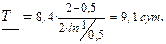
По формуле (2.38) вычислим Т_0,75 при q =0,9:

при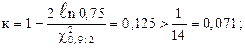

при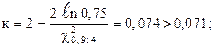

при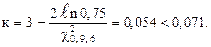

Поэтому выбираем к =2.

Тогда суммарная наработка

S₂=t₁+ 12 t₂ =5+12 х 7=89 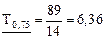сут;

сут.

Сравнивая полученные значения 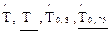с результатами, полученными в прим. 2.2 и 2.5, видим, что дополнительная информация о характере интенсивности отказов повышает точность получаемых оценок.

2.3. Оценивание показателей безотказности при испытании

с измерением определяющего параметра (величины износа)

случаев условие работоспособности машины можно определить такими параметрами, как износ и "прочность - нагружение". Такие параметры называются определяющими параметрами (ОП). В ряде

Модели отказов, использующие определяющие параметры, называют параметрическими моделями надёжности, а надёжность изделий, оцениваемую на основе этих моделей, - параметрической надёжностью.

В этом случае оценка параметрической надёжности изделия возможна по результатам измерения определяющих параметров, не дожидаясь появления отказов изделия, и появляется возможность прогноза уровня его надёжности.

Частными случаями моделей отказов, использующих определяющие параметры, являются модели отказов типа непревышений (допусковые модели). Для этой модели условие работоспособности изделия имеет вид:

А={UОD}; D=(U₀,U_d),

где U - определяющий параметр (величина износа), рассматриваемый в некоторый критический момент времени на интервале [ 0, t₀] (t₀ - заданная продолжительность функционирования изделия).

Запись А={UОD} означает, что мы имеем дело с событием А, заключающимся в том, что величина износа находится в допустимой области, ограниченной величиной допуска U₀, заданной ТУ, и максимально допустимой величиной износа U_d.

Это так называемая статическая (допусковая) модель, в которой точечная оценка вероятности безотказной работы, принимая, что величина износа имеет нормальный закон распределения, находится по формуле

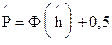, (2.41)

где 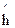- нормированный допуск

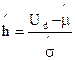, если D=(U₀,U_d). (2.42)

На рис. 2.1 представлена схема статической модели.

Определение НДГ и ВДГ вероятности безотказной работы осуществляется по формулам:

, (2.43)

где F(h) - функция Лапласа, определяемая из табл. 1, прил. Б;

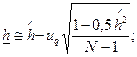(2.44) 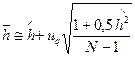, (2.45)

где 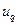- квантиль порядка q, определяемая из табл. 3, прил. Б.

Когда нет возможности производить измерения износа в отдельные моменты времени на интервале наблюдений I_t=[ 0, t]<[ 0, t₀], то в этом случае при проведении испытаний осуществляют подсчёт числа тех реализаций из их общего числа N, которые на промежутке I_t вышли за допуск [U], назначенный ТУ, или за некоторый контрольный, более жёсткий допуск [U]'.

t

t_н

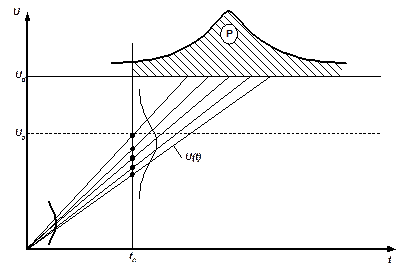
Рис.2.1. Статическая (допусковая) модель отказов

Считая случайный процесс изнашивания гауссовским со средним значением 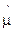и дисперсией 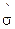, а значение [U] допуска (в допустимой области D=(U₀[U]) на U(t)) достаточно высоким, так, что поток выбросов U(t) за уровень [U] можно считать пуассоновским, тогда вероятность безотказной работы Р(t₀) на промежутке [ 0, t₀] можно представить в виде:

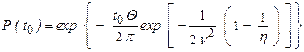, (2.46)

где 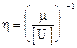- запас определяющего параметра U(t) по отношению к допуску на него;

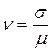- коэффициент вариации, известный на основе предварительных испытаний;

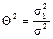- отношение дисперсии скорости изнашивания J(t) и самого процесса изнашивания U(t) (предполагается априори известной).

Для получения точечных и интервальных оценок вероятности безотказной работы воспользуемся биноминальным планом испытаний, при котором на испытания будут поставлены N образцов изделий в течение времени t₁=[ 0, t₀], t ₁< t₀ и зафиксировано d ₁ отказавших образцов.

При этом отказом изделия за промежуток t ₁ считается выход ОП (U (t) - величина износа) не за допустимый уровень [U], а за ужесточённый уровень [U]', когда [U] >[U]'. Показатель х₁ = [U]/[U]' называется коэффициентом "ужесточения" испытаний в момент t₁.

Контроль работоспособности машины производим в единственный момент времени t ₁(t ₁< t₀), например в момент профилактики.

Коэффициент "ужесточения" х₁ назначают из таких соображений, чтобы, как правило, имел место исход испытаний d ₁ =0.

Имея данные N₁ и d ₁ на момент t = t₁, находим точечную оценку

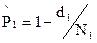(2.47)

Для наиболее частого случая, когда d ₁ =0:

. (2.48)

Затем определяют точечную оценку вероятности безотказной работы 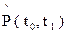по формуле

(2.49)

и НДГ вероятности безотказной работы

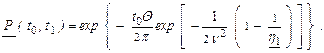(2.50)

где

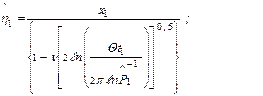
	(2.51)
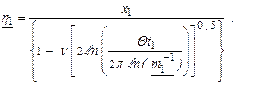
	(2.52)

Коэффициент вариации v и параметр Q оцениваются на основании априорных данных.

Пример 2.7.

Величина зазора U в шарнире универсального шпинделя на вкладышах скольжения по ТУ должна удовлетворять требованию [U]>U, где [U] =7 мм (допустимая величина зазора) в течение наработки t₀. По результатам испытаний N =4 шарниров универсальных шпинделей были получены следующие результаты по измерению зазора, мм: 5,4; 6,0; 6,2; 6,4. Требуется оценить вероятность безотказной работы шарнира универсального шпинделя за наработку t_d =30 сут (межремонтный период), если распределение U(t) принять нормальным.

Решение.

Находим оценки параметров m, s и h по формуле (2.42).

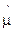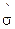=6; =0,6; 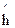=1,667.

По формуле (2.41) с использованием табл.1, прил. Б находим точечную оценку вероятности безотказной работы

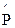=Ф(1,667)+0,5=0,951.

По формуле (2.43) и (2.44) находим НДГ вероятности безотказной работы q =0,9.

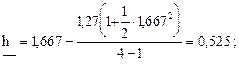
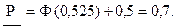
Глава 3. Оценивание показателей долговечности

3.1. Модели оценивания

Для характеристики долговечности объекта используются показатели, рассмотренные в гл.2 части I.

Для условий эксплуатации металлургических машин наиболее приемлемым является средний ресурс Т. Средний ресурс - это математическое ожидание ресурса, т.е. наработки объекта от начала его эксплуатации или её возобновления после капитального ремонта до перехода в предельное состояние.

При решении вопроса о плановой замене важное значение приобретает знание среднего остаточного ресурса Т(t), где t - наработка, после которой производится оценка данного показателя.

Оценивание среднего ресурса по результатам испытаний может быть сведено к оцениванию функции надёжности, т.е. к вероятности безотказной работы (ВБР) - Р(t)

.

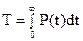Однако в ряде случаев, широко распространённых на практике, можно получить готовые выражения для оценки среднего ресурса непосредственно - без использования функции надёжности.

Исходными данными для оценки показателей долговечности изделия являются результаты испытаний (наблюдений) N образцов изделия.

В общем случае результаты таких испытаний представляются в виде:

– выборочных значений наработки до предельного состояния (отказа), r

t₁, t₂, јt _r;

– выборочных значений наработки до цензурирования, n

t₁,t₂, јt _n,

причём N = r + n.

Планы испытаний рассмотрены в гл. 8 части I, раздел 1.

Наиболее распространёнными являются планы [NUN] и [NUz].

По исходным результатам испытаний с числом возможной априорной информации о виде и характере закона распределения наработки до отказа находятся точечная оценка 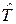ресурса и его доверительные границы на основе параметрической модели оценивания.

Параметрические модели оценивания были рассмотрены в гл.2 прил.А.

Оценивание среднего ресурса возможно и в том случае, если известна функция распределения определяющего параметра (например, функция изменения величины износа с течением времени).

Дата добавления: 2014-12-08