Пассажирских корреспонденций

Модели формирования матрицы межостановочных

Как уже отмечалось, решение задач информационного обеспечения процесса оптимизации МС на ЭВМ должно обеспечить этот процесс следующей основной информацией.

· Прежде всего, это матрица межостановочных (межузловых) корреспонденций (ММК), являющаяся моделью некой усредненной суточной (для будних дней) потребности населения города в передвижениях на ОПТ, детализирующей потребность в передвижениях на ОПТ до количества передвижений за сутки между всеми остановочными пунктами (транспортными узлами) города - 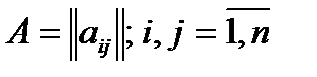, где 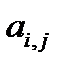- потенциальное количество передвижений, совершаемых за сутки с использованием ОПТ от i-го до j-го остановочного пункта (транспортного узла).

Следует заметить, что при моделировании реализации этих передвижений на различных вариантах МС, часть из этих передвижений может быть реализована пешком. Это происходит в тех случаях, когда временные затраты на соответствующие пешие передвижения будут меньше, чем на те же передвижения, но с использованием ОПТ, либо в тех случаях, когда в рассматриваемом варианте МС отсутствуют транспортные связи ОПТ межу корреспондирующими ОП и передвижения вынужденно реализуются пешком.

· Должны быть определены узлы, в которых возможно размещение начально-конечных пунктов маршрутов (за основу, как правило, берется существующее размещение конечных ОП), а также возможные технологические ограничения на маршруты.

· Проектировщики МС должны располагать информацией о маршрутных пассажиропотоках существующей МС (перечень этой информации смотри подробнее в промежуточном отчете по разделам №2,3 программы работ договора №357), о пропускной способности участков и узлов ТС (в данном случае как перекрестков, так и ОП), о существующей интенсивности движения на наиболее загруженных участках и узлах ТС (подробнее смотри в промежуточном отчете по разделам №7,8 программы работ договора №357).

· Должны быть заданы ресурсные ограничения на количество ПС по видам транспорта, по его структуре по вместимости и по маркам ПС.

· Должны быть заданы показатели удельных эксплуатационных расходов по всем маркам ПС, которые работают на существующих маршрутах, а также по тому ПС, который предполагается использовать на новой МС. Эти показатели должны позволить дать оценку изменения эксплуатационных расходов для различных вариантов МС.

· Кроме этого для сравнительных экономических расчетов необходимы данные о стоимости ПС различных марок, чтобы получать оценки изменений капитальных вложений в ПС при различном количестве и структуре парка ПС.

Из всего названного перечня необходимой информации наибольшие проблемы связаны с заданием матрицы корреспонденций 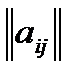- ММК.

ММК получают либо путем обследования спроса на транспортные передвижения (опросные, анкетные обследования), либо путем математического моделирования, либо используя то и другое.

Математическое моделирование пассажирских корреспонденций в городах связано главным образом с потребностями планирования развития транспортных систем городов и на практике используется в основном на таких стадиях градостроительного проектирования, как разработка генеральных планов развития городов и разработка комплексных транспортных схем городов. Наибольшее распространение при этом получили так называемые «гравитационные» модели, а затем «энтропийные» модели. В соответствии с гравитационной моделью величина корреспонденции между i- м и j -м микрорайонами – x_ij определяется как

, (15.39)

где 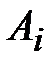- объем передвижений, возникающих в i- м микрорайоне;

Вj – объём передвижений, заканчивающихся в j-м микрорайоне;

- убывающая функция от времени сообщения между микрорайонами i и j.

Очевидно, что данная модель обеспечивает выполнение лишь одного из двух балансовых ограничений – ограничения по числу отправлений из микрорайона:

. (15.40)

Для того, чтобы выполнялись ограничения по числу прибытий, то есть чтобы

, (15.41)

предложены различные процедуры балансировка матрицы корреспонденций, наиболее распространенной среди которых является балансировка по методу Ю.А. Шацкого, Ю.З. Шершевского.

Как показали исследования, этот метод дает в качестве предельной матрицу корреспонденций, максимизирующую взвешенную относительно априорного предпочтения энтропию

, (15.42)

при ограничениях 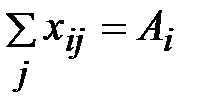; ; 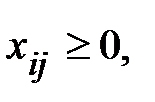(15.43)

где P_i,j – величины априорного предпочтения, которые часто полагаются равным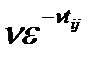и или .

Следует заметить, что если значение определить таким образом, чтобы решение задачи (15.42), (15.43) обеспечило заданное среднее время или среднюю дальность передвижения пассажиров

, (15.44)

то оказывается, что эти корреспонденции могут быть получены также путем решения задачи

, (15.45)

при ограничениях (15.43), (15.44).

Рассмотрение в различных работах целого ряда моделей коллективного поведения, таких, например, как модель стихийной миграции населения в городах, возникающей при обмене жилья, модель распределения массы претендентов по некоторому множеству состояний, приводило к модели максимизации взвешенной энтропии. Это позволило сделать вывод о рассмотрении принципа максимума взвешенной энтропии, как подход к решению широкого класса задач прогноза массового поведения людей при распределении их по множеству физически сопоставимых состояний. В ряде работ показано, что с использованием моделей максимизации энтропии может быть исследован еще более широкий класс систем, названных стохастическими коммуникационными системами.

Сложность использования гравитационной модели обусловлена тем, что гравитационная модель должна калиброваться на основе физических корреспонденций для какого-либо конкретного города. Меньшие трудности, связанные с калибровкой, вызывает модель максимизации энтропии. При этом фактические корреспонденции описываются с помощью модели максимизации энтропии с той же точностью, что и с помощью гравитационной модели, хотя последняя подгоняется путем калибрования по фактическим корреспонденциям.

Модель максимизации энтропии выражается следующим образом:

; (15.46)

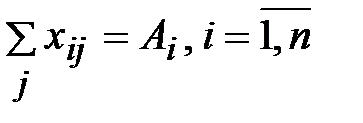; (15.47)

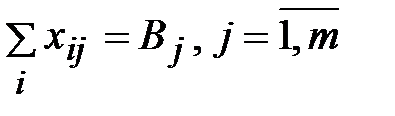; (15.48)

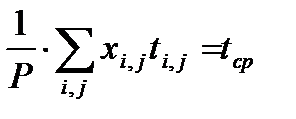, (или ), (15.49)

.

В данной модели требуется максимизировать выражение (15.46) при ограничениях (15.47)-(15.49). Ограничения (15.47) и (15.48) являются условиями баланса корреспонденций, а ограничение (15.49) требует определения корреспонденций таким образом, чтобы прогноз среднего времени (среднего расстояния) следования на работу равнялся фактическому времени .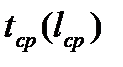

Это ограничение является существенным, поскольку оно даже при недостаточной точности получения самих корреспонденций с помощью модели, не искажает общий объем транспортной работы в городе, что может произойти при моделировании с помощью гравитационной модели.

Модель максимизации энтропии основана на том предположении, что из всевозможных корреспонденций , удовлетворяющих условиям (15.47) – (15.49), наиболее вероятными являются те, которые максимизируют энтропию рассматриваемой системы, т.е. выражение (15.46).

В модели максимизации энтропии искомыми величинами являются корреспонденции , остальные же величины () считаются заданными. Для нахождения условного экстремума в подобных задачах используется обычно метод множителей Лагранжа. При этом максимизация функции (15.46) с ограничениями (15.47)-(15.49) заменяется максимизацией вспомогательной функции L:

, (15.50)

где - неопределенные множители Лагранжа.

Приравнивая частные производные функции L к нулю, получим

или

(15.51)

Произведя в выражении (15.51) подстановки , , 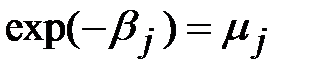и учитывая ограничения (15.47) –(15.49), после некоторых преобразований получим следующую систему уравнений:

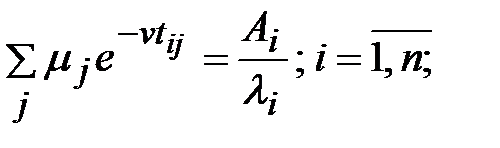(15.52)

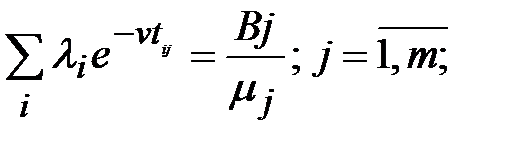(15.53)

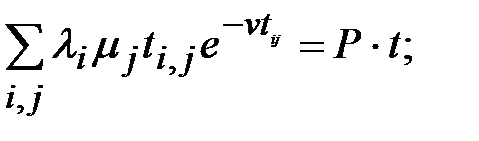(15.54)

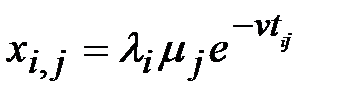. (15.55)

Таким образом, для расчета корреспонденций необходимо решить систему (n+m+1) уравнений (15.52) – (15.54) относительно 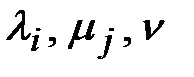. Решение данной системы можно осуществить итерационным методом, описанным, например в [ ]. Для этого в уравнениях (15.52), (15.53) необходимо задать значение 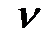(например, 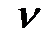=0) и определить для него и следующим образом:

выбрать исходные значения для (например, =1, );

из уравнения (15.52) определить , соответствующие выбранным ;

из уравнения (15.53) определить новые , соответствующие полученным и т.д. до достижения требуемой точности. Далее из уравнения (15.54) 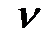, соответствующее полученным , по описанной выше процедуре и т.д. до достижения заданной точности.

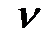Для нахождения из уравнения (15.50) можно применить один из численных методов решения подобных уравнений, например, метод Ньютона, по которому корень уравнения F(z) = 0 находится следующим образом

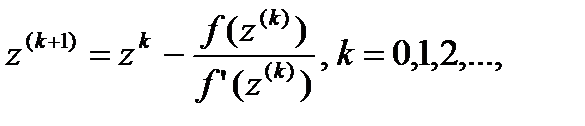(15.56)

где 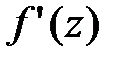- производная .

Именно такой подход и предлагается реализовать при формировании суточной матрицы пассажирских корреспонденций для г. Омска, но не для получения всей ММК, а только ее части. Отказ от моделирования всей ММК с помощью «энтропийной» модели связан со стремлением получить более достоверную ММК, нежели это возможно при использовании «энтропийной» модели.

Первая из этих матриц - ММК-1 представляет собой матрицу только трудовых и учебных корреспонденций. Данная матрица формируется на основе анкетных опросов трудящихся, студентов ВУЗов и учащихся ССУЗов об остановочных пунктах отправлений и прибытий, от которых и до которых совершаются трудовые (учебные) передвижения с использованием ОПТ.

Для трудящихся (учащихся), которые не охвачены анкетным опросом, для формирования корреспонденций используются деперсонифицированные адреса проживания, предоставляемые предприятиями (учебными заведениями), либо региональным отделением пенсионного фонда России (ПФР).

Вторая матрица – ММК-2 представляет собой скорректированную матрицу межостановочных (межузловых) корреспонденций, которые формируются на основе таблично-опросного метода обследования пассажиропотоков МТ с размещением учетчиков в ПС. Корректировка матрицы корреспонденций на МТ – ММК(МТ) состоит в том, что из этой матрицы исключаются корреспонденции, уже вошедшие в ММК-1. Учитывая, что в исходной ММК(МТ) присутствуют все виды передвижений (по целям), включая как трудовые, учебные, так и культурно-бытовые и другие, а значит частично и те, которые уже учтены в ММК-1, то естественно, для выделения из ММК(МТ), прежде всего, культурно-бытовых, деловых, а также не учтенных в ММК-1 трудовых и учебных корреспонденций, необходимо из ММК(МТ) удалить корреспонденции, уже вошедшие в матрицу трудовых (учебных) передвижений - ММК-1.

Заметим, что как показывают исследования по г. Омску, в ММК(МТ) входят около половины корреспонденций, учтенных в ММК-1.

Несмотря на то, что ММК (МТ) получена из помаршрутных корреспонденций, а не сетевых, необходимо иметь в виду следующее. Как показывает проведенный в рамках настоящей НИР анализ пересадочности передвижений, которая исследовалась путем опроса пассажиров на 48-ми остановочных пунктах, являющихся основными пересадочными пунктами в городе, уровень пересадочности пассажиров, использующих маршрутные такси, вдвое ниже, по сравнению с передвижениями, совершаемыми с использованием муниципального транспорта.

Следовательно, погрешность замены сетевых корреспонденций маршрутными корреспонденциями на МТ при общем коэффициенте пересадочности на уровне 1,2-1,25 (данный показатель получен для г.Омска при упомянутом выше исследовании пересадочности, а также при обработке данных анкетных опросов по трудовым (учебным) передвижениям), будет составлять порядка 10-12%, что является очень хорошим показателем при моделировании корреспонденций.

Наконец, третья матрица - ММК-3 представляет собой матрицу, получаемую с помощью «энтропийной» модели (15.46)-(15.49), в которой и 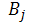в ограничениях (15.47), (15.48) и в ограничении (15.49) определяются следующим образом:

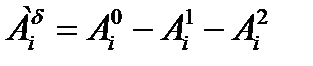; (15.57)

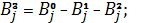
(15.58)

где 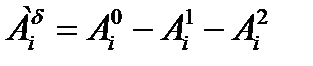- общее число отправлений из i -го транспортного узла (ОП) во все другие узлы (ОП) соответственно в ММК, ММК-1, ММК-2 и ММК-3;

- общее число прибытий в j -й узел (ОП) из всех других узлов (ОП) соответственно в ММК, ММК-1, ММК-2 и ММК-3;

определяется из условий (15.59), (15.60):

(15.59)

(15.60)

где - общее количество передвижений соответственно в ММК, ММК-1, ММК-2 и ММК-3;

- средняя дальность передвижений, определяемая соответственно по ММК, ММК-1, ММК-2 и ММК-3;

– средняя маршрутная дальность поездок, полученная по результатам обследования маршрутных пассажиропотоков на всех видах ОПТ;

- оценка коэффициента пересадочности на существующей МС, получаемая на основе анкетных исследований трудовых (учебных) передвижений, опроса пассажиров о пересадочности в основных пересадочных ОП, а также на основе моделирования реализации передвижений на существующей МС.

Из выражений (15.59), (15.60) следует, что

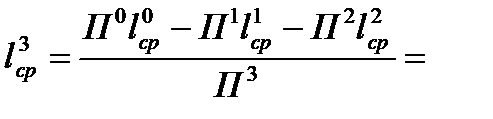
(15.61)

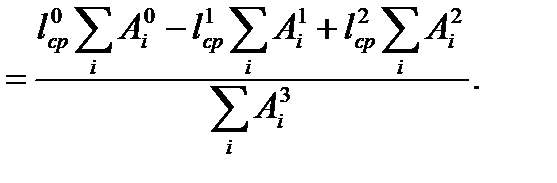
Заметим, что если n=m, то

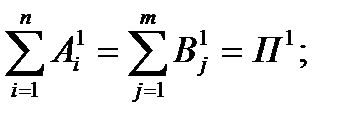
(15.62)

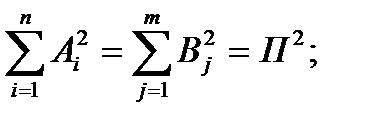
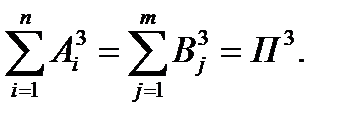
Общее количество передвижений 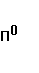задается из следующего условия:

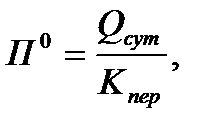(15.63)

где 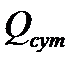- среднесуточный объем перевозок на ОПТ, оценка которого определяется по результатам обследования маршрутных пассажиропотоков на всех видах ОПТ.

Величины 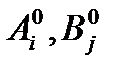для всех i, j определяются следующим образом.

На основе обследований маршрутных пассажиропотоков рассчитывается количество пассажиров, входящих и выходящих 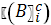на каждой остановке (транспортном узле).

Далее рассчитывается общее среднесуточное количество пересадок 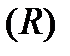на действующей МС и количество пересадок в каждом транспортном узле (на каждой остановке) r_i:

(15.64)

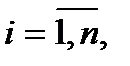при этом 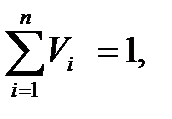(15.65)

где - вес транспортного узла (ОП) по числу пересадок (устанавливается по результатам трех видов исследований: по результатам обработки данных анкетного опроса трудящихся (учащихся) о местах пересадки при совершении трудовых (учебных) передвижений; по результатам опроса пассажиров о пересадочности на основных пересадочных ОП; по результатам предварительного моделирования распределения корреспонденций на существующей МС).

Если обозначить:

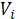– оценка при исследовании трудовых передвижений; причем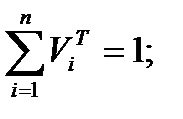

– оценка 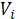при исследовании трудовых передвижений, полученная на основе опроса пассажиров в транспортных узлах; при этом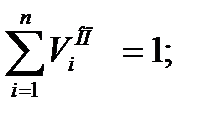

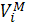– оценка 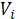при исследовании трудовых передвижений, полученная на основе предварительного моделирования распределения корреспонденций на существующей МС,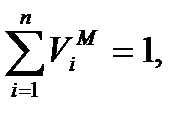

то в качестве модели задания 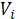можно принять следующую:

(15.66)

где - экспертно задаваемый приоритет использования различных видов оценок пересадочности в транспортных узлах ( - приоритет оценок 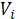, сделанных по трудовым передвижениям; - приоритет оценок 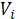, сделанных по опросам пересадочности в транспортных узлах; - приоритет оценок 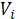, сделанный по результатам моделирования распределения корреспонденций), причем приоритеты должны быть заданы таким образом, чтобы

Величины 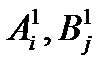определяются в результате формирования матрицы ММК-1.

Величины определяются в результате формирования матрицы ММК-2.

Величины 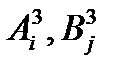определяются, как уже указывалось, в соответствии с выражениями (15.57), (15.58).

Сформированная в результате ММК изложенным выше способом, должна обеспечить значительно более высокий уровень ее детальности и достоверности по сравнению со всеми известными на сегодня способами ее формирования, т.к. практически на 70% она образуется на реальных корреспонденциях и только на 30% - моделируется с помощью моделей, аналогичных тем, которые использованы для 100%-гомоделирования матриц межрайонных корреспонденций при совершенствовании МС (например в г. Санкт-Петербурге(2003г.), гг. Харькове, Сумы, Херсоне, Мелитополе (2000-2003гг.)).

Единственная особенность формирования ММК для Украинских городов с помощью гравитационной модели - это новая процедура балансировки корреспонденций (выполнение обычных ограничений (15.40), (15.41)) обеспечивается не с использованием метода Шацкого-Шершевского, а предложен собственный подход: получать корреспонденции как результат решения оптимизационной задачи по минимизации суммы квадратов отклонений искомых (сбалансированных) корреспонденций от корреспонденций, получаемых в соответствии с зависимостью (15.39).

При моделировании транспортных передвижений с помощью «энтропийной» модели в Санкт-Петербурге, вводились дополнительные ограничения для отдельных групп предприятий (по районам города).

Дата добавления: 2014-12-08