Наивероятнейшее число наступлений события 1 страница

Наивероятнейшее число m₀ определяется из двойного неравенства

np - q 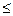m₀ 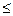np + p (9)

Формула Пуассона (лучше использовать при .)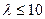

Теорема: Если вероятность p наступления события А в каждом испытании постоянна и близка к нулю (р 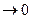), а число независимых испытаний n достаточно велико (), причем произведение np стремится к постоянному числу то вероятность P_n(k) того, что в n независимых испытаниях событие А наступит k раз, приближенно равна: 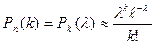(11)

Локальная теорема Муавра-Лапласа (рекомендуется применять при npq ).

Пусть в серии из n независимых испытаний вероятность наступления события А в каждом испытании равна р (0<p<1), q=1-p, . Если и величина является ограниченной, тогда (12).

Таблица значений функции приведена в приложении. Функция является четной, т.е = , монотонно убывающей при х>4 практически .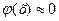

Интегральная теорема Муавра-Лапласа (удобно применять при npq ).

Если n – велико, а р – отлично от 0 и 1, то

где - функция Лапласа. Таблица значений функции 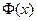приведена в приложении. Функция 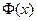является нечетной, т.е =- 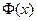.Если х>4, то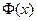 в силу монотонного возрастания функции .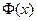

Решение задач:

Полагая, что вероятность поражения мишени при одном выстреле равна 0,6, найти вероятности следующих событий:

1) а) при 12 выстрелах мишень будет поражена 7 раз;

б) при 12 выстрелах мишень будет поражена менее 4 раз;

в) при 12 выстрелах мишень будет поражена не более 8 раз;

2) Наивероятнейшее число выстрелов, которые поразят мишень при 125 сделанных выстрелах. И вероятность этого числа попаданий.

3) При 200 выстрелах мишень будет поражена не менее 110, но не более 130 раз.

4) При 200 выстрелах мишень будет поражена не более 110 раз;

5) При 200 выстрелах мишень будет поражена не менее 115 раз.

6) На стрельбы пришла Полина Александровна. Для нее вероятность попадания в мишень равна 0,04. Найти вероятность того, что из 200 выстрелов Полина Александровна попадет в мишень 10 раз.

Решение:

1) воспользуемся формулами Бернулли:

а) Р₁₂(7)= ;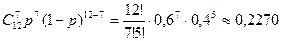

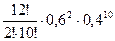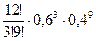
б) при 12 выстрелах мишень будет поражена менее 4 раз означает, что мишень будет поражена 0, 1, 2 или 3 раза. Ищем Р₁₂(0)+Р₁₂(1)+Р₁₂(2)+Р₁₂(3)= + + + 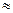0,000017+0,000302+0,002491+0,012457=0,12738.

в) при 12 выстрелах мишень поражена не более 8 раз означает, что она поражена 0,1,2,…,8 раз. Вычисление каждой из этих вероятностей и их последующее суммирование приведет к очень громоздким вычислениям. Противоположным событием будет событие, состоящее в том, что мишень поражена более 8 раз, т.е. 9, 10, 11 или 12.

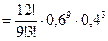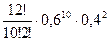
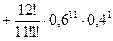
Найдем Р₁₂(9)+Р₁₂(10)+Р₁₂(11)+Р₁₂(12)= + 0,14189+0,06385+0,01741+

+0,002177=0,225331. Нас интересует вероятность противоположного события, т.е. искомая вероятность равна 1- (Р₁₂(9)+Р₁₂(10)+Р₁₂(11)+Р₁₂(12)) .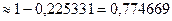

2) Наивероятнейшее число выстрелов, которые поразят мишень при 125 сделанных выстрелах. Воспользуемся формулой: np - q 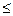m₀ 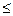np + p. Подставив в формулу n=125, р=0,6, q=0,4, получим 74,6 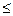m₀ 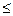75,6. Следовательно, наивероятнейшее число попаданий будет равно 75.

Найдем 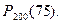Т.к. n=200 достаточно велико (условие ), применяем локальную теорему Муавра-Лапласа. Сначала определим 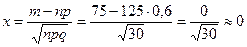.Тогда по формуле .

Значение 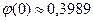найдено по табл.1 приложений.

3) Найдем вероятность того, что при 200 выстрелах мишень будет поражена не менее 110, но не более 130 раз. Так как количество выстрелов и количество попаданий достаточно велико, применение формулы Бернулли будет связано с большими трудностями. Применим интегральную формулу Муавра-Лапласа. Здесь n=200, р=0,6,q=0,4, k₁=110, k₂=130.

.

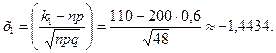
Теперь по формуле (15) и учитывая свойства Ф(х), получим

Р₂₀₀

(по таблице 2 приложений, Ф(1,44) ).

4) При 200 выстрелах мишень будет поражена не более 110 раз. Ищем Р₂₀₀ .. Применим интегральную формулу Муавра-Лапласа. Здесь n=200, р=0,6,q=0,4, k₁=0, k₂=110.

.

5) Вероятность того, что при 200 выстрелах мишень будет поражена не менее 115 раз будем искать, также применяя интегральную формулу Муавра-Лапласа.

Задачи в классе. Здесь n=200, р=0,6,q=0,4, k₁=115, k₂=200.

.

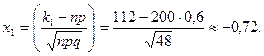
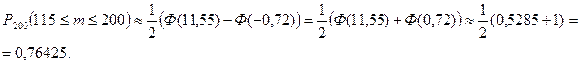
6) На стрельбы пришла Полина Александровна. Для нее вероятность попадания в мишень равна 0,04. Найти вероятность того, что из 200 выстрелов Полина Александровна попадет в мишень 10 раз.

р=0,04, q=0,96, n=200, m=10.

Т.к. n=200 достаточно велико (условие ), применяем теорему Пуассона 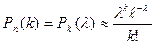, где 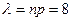. . Значение Р₁₀(8) берем из таблицы в приложении III.

ВАРИАНТЫ ЗАДАЧ

Вариант 1

1. А). Сколько перестановок можно получить из букв слова ВАЛЕТ?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?

1. А). Сколько перестановок можно получить из цифр числа 125367266?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?

1. Из букв слова ПРОГУЛКА составляются пятибуквенные слова.
   А) Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
   
   
2. Решить уравнение
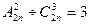
3. В ящике содержится 10 деталей, среди которых 3 нестандартные. Определить вероятность того, что в наудачу отобранных 6 деталях окажется а) ровно две нестандартные; б) не более двух нестандартных.

1. Агентство по страхованию автомобилей разделяет водите­лей по 3 классам: класс Н₁ (мало рискует), класс H₂ (рискует средне), класс H₃ (рискует сильно). Агентство предполагает, что из всех водителей, застраховавших автомобили, 30% принадлежат к классу 50% — к классу H₂ и 20% — к классу H₃. Вероятность того, что в течение года водитель класса Н₁ попадет хотя бы в одну аварию, равна 0,01, для водителя класса H₂ эта вероятность равна 0,02, а для водителя класса H₃ — 0,08. Водитель А страхует свою машину и в течение года попадает в аварию. Како­ва вероятность того, что он относится к классу H1?
2. Транзисторный радиоприемник смонтирован на 9 полупроводниках, для которых вероятность брака равна 0,05. приемник отказывает при наличии не менее двух бракованных полупроводников. Найти вероятность того, что: а) откажут ровно 5 полупроводников; б) приемник будет работать; в) приемник откажет.

1. Фарфоровый завод отправил на базу 10000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0001. Найдите вероятность того, что на базу придут ровно 3 негодных изделия.

1. Известно, что левши составляют примерно 1%. оценить вероятность того, что среди 500 человек окажется а) четверо левшей; б) левшей не менее 80, но не более 150 человек.

Вариант 2

1. А). Сколько перестановок можно получить из букв слова БОЧКА?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?

1. А). Сколько перестановок можно получить из цифр числа 245752235?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?

1. Из букв слова ПРОСЬБА составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
2. Решить уравнение
3. Среди десяти билетов выигрышными являются четыре. Определить вероятность того, что среди взятых наудачу пяти билетов окажется а)три выигрышных; б) не более трех выигрышных

1. В студенческом стройотряде 3 бригады первокурсников и одна — второкурсников. В каждой бригаде первокурсников 6 юношей и 4 девушки, а в бригаде второкурсников 4 юношей и 4 девушки. По жеребьевке из отряда выбрали одну из бригад и из нее одного человека для поездки в город, а) Какова вероят­ность того, что выбран юноша? б) Выбранный человек оказался юношей. Какова вероятность, что он первокурсник?
2. Радиоэлектронный комплекс самолета-бомбардировщика включает в себя 10 объектов. Вероятность работы каждого объекта равна 0,9. Объекты выходят из строя независимо один от другого. Найти вероятность того, что: а) откажет хотя бы один объект; б) откажут ровно два объекта; в) откажут не менее двух объектов.
3. Радиоэлектронный комплекс самолета-бомбардировщика включает в себя 10 объектов. Вероятность работы каждого объекта равна 0,9. Объекты выходят из строя независимо один от другого. Найти вероятность того, что: а) откажет хотя бы один объект; б) откажут ровно два объекта; в) откажут не менее двух объектов.

1. Полагая, что вероятность поражения мишени при одном выстреле равна 0,6, найти вероятность того, что а) при 200 выстрелах мишень окажется поражена 110 раз; б) мишень будет поражена от 60 до 140 раз.

Вариант 3

1. А). Сколько перестановок можно получить из букв слова АЛЬБОМ?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?

1. А). Сколько перестановок можно получить из цифр числа 345642353?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?

1. Из букв слова ПРОСТЫНЯ составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?

1. Решить уравнение
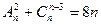
2. В букете, состоящем из 9 цветов 4 красных цветка, остальные синие. Наудачу берется 5 цветов. Определить вероятность того, что красных цветов среди них будет а) ровно 2 штуки; б) не более двух.
3. В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих шаров наудачу взят один шар. а)Найдите вероятность того, что взят белый шар.б) Выбранный шар оказался белым. Какова вероятность, что он взят из первой урны?
4. Наблюдениями установлено, что в некоторой местности в июле в среднем бывает 12 дождливых дней. Какова вероятность того, что из восьми случайно выбранных в этом месяце дней а) ровно три окажутся дождливыми; б) дождливыми окажутся хотя бы два дня; в) дождливыми будут не более 7 дней?
5. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени t равна 0,002. Найдите вероятность того, что за время t откажут ровно 3 элемента.

1. Вероятность того, что станок-автомат произведет годную деталь, равна 9/11. за смену было изготовлено 330 деталей. Определить вероятность того, что среди них а) 40 бракованных; б) бракованных деталей не более 40, но не менее 2.

Вариант 4

1. Сколько перестановок можно получить из букв слова ТЕСАК?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?

1. А). Сколько перестановок можно получить из цифр числа 768987864?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?

1. Из букв слова ПРОЕКЦИЯ составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
2. Решить уравнение

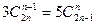
1. В студенческой группе 15 человек, из которых 5 девушек, а остальные – юноши. Деканат дал студентам этой группы 5 билетов на концерт группы «Тылобурдо». Найти вероятность, что а)3 билета достанутся девушкам; б) не менее трех билетов достанутся девушкам.
2. 70% учащихся в Ижгту — юноши. 80% девушек и 60% юношей имеют билеты на КВН. В деканат принесли кем-то потерянный билет. Какова вероятность того, что этот билет при­надлежал девушке? Юноше?
3. Рабочий обслуживает 12 однотипных станков. Вероятность, что станок потребует внимания рабочего в течение промежутка времени Т, равна 1/3. Найти вероятность того, что за время Т а) 4 станка потребуют внимания рабочего; б) менее 4-х станков.потребуют внимания рабочего; в) хотя бы 4 станка потребуют внимания рабочего.

1. Вероятность нарушения герметичности банки в некоторой партии консервных банок равна 0,0004. Вычислите вероятность того, что среди 2000 банок окажутся с нарушением герметичности не более 3.
2. Вероятность того, что деталь не прошла проверку ОТК равна р = 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных а) ровно 60; б) от 70 до 100.

Вариант 5

1. А). Сколько перестановок можно получить из букв слова САМОЛЕТ?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?

1. А). Сколько перестановок можно получить из цифр числа 465768756?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?

1. Из букв слова ПРОГУЛКА составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?

1. Решить уравнение
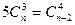
2. У Малыша в кульке лежали 12 конфет: 5 карамелек и 7 шоколадных. Карлсон не глядя запустил в кулек руку и достал 8 конфет. Найти вероятность того, что у Карлсона в руке оказалось а) 6 шоколадных конфет и 2 карамельки; б) карамелек оказалось не более 2.
3. Бросается монета, и если она падает так, что сверху ока­зывается герб, вынимаем один шар из урны I; в противном случае — из урны II. Урна I содержит 4 красных и 1 белый шар. Урна II содержит 1 красный и 3 белых шара, а) Какова вероятность того, что вынутый шар красный? б) Какова вероятность того, что шар вынимался из I урны, если он оказался красным?
4. Китайский завод изготавливает изделия, каждое из которых с вероятностью 1/3 оказывается дефектным. Для контроля продукции выбирается 6 изделий. Найти вероятность того, что а) ни в одном изделии не будет дефекта; б) не менее чем в двух изделий будет обнаружен дефект; в) ровно в трех изделиях будет дефект.

1. Вероятность появления брака при автоматической обработке деталей равна 0,003. Найдите вероятность того, что среди 1000 деталей только 4 детали будут бракованными.

1. Вероятность выхода конденсатора из строя в течение времени t равна 0,25. Вычислите вероятность того, что за этот промежуток времени из имеющихся 150 конденсаторов выйдет из строя а) ровно 60 конденсаторов; б) от 40 до 80 конденсаторов.

Вариант 6

1. А). Сколько перестановок можно получить из букв слова СВЁРТОК?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
   
   
2. А). Сколько перестановок можно получить из цифр числа 475674658?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
   
   
3. Из букв слова ПРИМОЧКА составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
   
   
4. Решить уравнение .
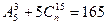5. Из 10 студентов 6 имеют спортивные разряды. Найти вероятность того, что среди выбранных наудачу 5 студентов спортивный разряд имеют а)3 человека; б) менее трех человек.
6. На радиозаводе машина А производит 40% всех радиостанций, а машина В — 60%. В среднем 9 единиц из 1000 еди­ниц продукции, произведенных машиной А, оказывается браком, а у машины В — брак 2 единицы из 500. Некоторая радиостанция, выбранная случайным образом из дневной продукции, оказалась браком. Какова вероятность того, что она произведена на машине В?
7. Баскетболист делает 5 бросков мячом в корзину. Вероятность попадания мяча при каждом броске одинакова и равна 0,4. найти вероятность того, что а) баскетболист ровно 4 раза попадет мячом в корзину; б) попаданий в корзину будет менее четырех; в) попаданий мячом будет не более 5.
8. Вероятность попадания в цель при каждом выстреле равна 0,001. Найдите вероятность попадания в цель двумя и более выстрелами при залпе в 5000 выстрелов.

1. При штамповке металлических клемм получается в среднем 90% годных. Найдите вероятность того, что среди 900 клемм окажется от 700 до 820 годных.

Вариант 7

1. А). Сколько перестановок можно получить из букв слова ТЕРМОС?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
   
   
2. А). Сколько перестановок можно получить из цифр числа 384576985?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
   
   
3. Из букв слова ПРИРОСТ составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
   
   
4. Решить уравнение .
5. В лотерее «Спортлото 6 из 30» участник лотереи, правильно угадавший 4, 5 или 6 видов спорта из 30, получает денежный приз. Найти вероятность того, что данный участник угадает а) 5 видов спорта; б) получит денежный приз.

1. В группе из 20 стрелков имеются 4 отличных, 10 хороших и 6 посредственных стрелков. Вероятность попадания в цель при одном выстреле для отличного стрелка равна 0,9, для хорошего — 0,7, для посредственного — 0,5. Найдите вероятность того, что: а) наудачу выбранный стрелок попадет в цель; б) 2 наудачу вы­бранных стрелка попадут в цель.в) Цель поражена. Найти вероятность, что ее поразил хороший стрелок
2. Среди коконов некоторой партии 30% цветных. Какова вероятность того, что среди 10 отобранных коконов а) цветных будет 3 кокона; б) цветных коконов будет не менее семи; в) цветных коконов будет не более 8.
3. На базе получено 10000 электроламп. Вероятность того, что в пути лампа разобьется, равна 0,0003. Найдите вероятность того, что среди полученных ламп будет пять ламп разбито.

1. Вероятность случайным образом отобранному изделию оказаться стандартным равна 0,8. Найдите вероятность того, что среди 225 взятых наугад изделий а) 180 окажутся стандартными; б) Стандартными окажутся от 155 до 200 изделий.

Вариант 8

1. А). Сколько перестановок можно получить из букв слова ТАНЕЦ?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
   
   
2. А). Сколько перестановок можно получить из цифр числа374694634?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
   
   
3. Из букв слова ПРОБКА составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
   
   
4. Решить уравнение
5. В аудитории находятся 25 студентов. 10 из них изучают английский язык, а остальные 15 – французский. Случайным образом для уборки территории отбираются 5 студентов. Найти вероятность того, что среди них а) ровно 3 изучают английский язык; б) студентов изучающих французский больше.

1. Агентство по страхованию автомобилей разделяет водите­лей по 3 классам: класс Н₁ (мало рискует), класс H₂ (рискует средне), класс H₃ (рискует сильно). Агентство предполагает, что из всех водителей, застраховавших автомобили, 30% принадлежат к классу 50% — к классу H₂ и 20% — к классу H₃. Вероятность того, что в течение года водитель класса Н₁ попадет хотя бы в одну аварию, равна 0,01, для водителя класса H₂ эта вероятность равна 0,02, а для водителя класса H₃ — 0,08. Водитель А страхует свою машину и в течение года попадает в аварию. Како­ва вероятность того, что он относится к классу H₂?
2. По каналу связи передается 8 сообщений. Каждое из них независимо от других с вероятностью 0,2 искажается помехами. Найти вероятности следующих событий: а) из 8 событий ровно 5 искажаются помехами; б) искажаются помехами не более половины всех передаваемых сообщений; в) помехами искажается более 6 сообщений.

1. Найдите вероятность того, что среди 200 изделий окажется ровно три бракованных, если в среднем бракованные изделия составляют 1%.

1. В цехе имеется 80 станков, работающих независимо друг от друга. Для каждого станка вероятность быть включенным равна 0,9. Вычислите вероятность того, что в некоторый момент времени включенными окажутся а) ровно 50 станков; б) от 60 до 75 станков.

Вариант 9

1. А). Сколько перестановок можно получить из букв слова КУЛЕБЯКА?
   Б). Сколько перестановок будет заканчиваться на гласную букву для четных вариантов, на согласную букву – для не четных вариантов?
   
   
2. А). Сколько перестановок можно получить из цифр числа 475638575?
   Б). Сколько перестановок будет начинаться с четной цифры для четных вариантов, с нечетной цифры – для нечетных вариантов?
   
   
3. Из букв слова ПРИМЕР составляются пятибуквенные слова.
   А).Сколько таких слов можно получить?
   Б) Сколько таких слов начинается с буквы П?
   В) А если слова содержат не менее 5 букв?
   
   
4. Решить уравнение
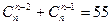
5. В конкурсе мисс ИжГТУ участвовало 13 девушек. Среди них было 6 блондинок и 7 брюнеток. Первокурсник ИВТ факультета пригласил в кино их всех, но пришли только 5 девушек. Найти вероятность того, что первокурсник смотрел кино а) 5 блондинками; б) двумя блондинками и тремя брюнетками.
6. В каждой из 3 урн по 6 черных и 4 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найдите вероятность того, что шар, извлеченный затем из третьей урны, окажется белым.
7. Игральная кость подбрасывается 9 раз. Найти вероятность того, что а) шестерка выпадет 3 раза; б) шестерка выпадет более трех раз; в) шестерка выпадет не более семи раз.
8. Устройство состоит из 1600 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени t равна 0,001. Найдите вероятность того, что за время t 4 элемента.

Дата добавления: 2014-12-08