D – преобразования

При использовании метода однородных координат точка в 3-х мерном пространстве представляется четырьмя составляющими h_x, h_y, h_z, h, где h - может принимать любое значение. На практике h=1, что соответствует нормализованным координатам (x, y, z, 1).

Для 3D - преобразования (X^*, Y^*, Z^*, 1) = (X, Y, Z, 1) * | A |,

где (X, Y, Z, 1) - координаты исходной точки, | A | - матрица преобразования, (X^*, Y^*, Z^*, 1) - координаты точки после преобразования.

Матрица вращения вокруг оси Х: 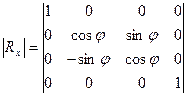.	Матрица вращения вокруг оси Y:
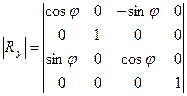
Матрица вращения вокруг оси Z: 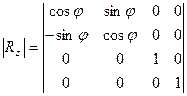.	Матрица растяжения: .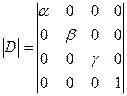

Матрица отражения относительно плоскости XY: .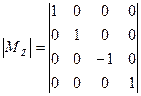

Матрица отражения относительно плоскости YZ: .

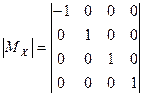Матрица отражения относительно плоскости ZX: .

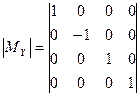Матрица переноса: .

В качестве примера рассмотрим матрицу вращения А одновременно вокруг двух осей (относительно оси Y на угол w, а относительно оси Х на угол f) с последующим проектированием вдоль оси Z.

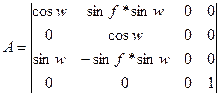
Удаление невидимых линии и поверхностей

Необходимость удаления невидимых линий, ребер, поверхностей или объемов обусловлена прежде всего двумя причинами:

1. Наглядность.

2. Неоднозначность.

Несмотря на кажущуюся простоту, эта задача является достаточно сложной и требует зачастую больших объемов вычислений. В качестве возможных видов проектирования обычно рассматривается параллельное либо центральное (перспективное) проектирование. Проектирование осуществляется на картинную (визуальную) плоскость экрана. Проектирующий луч к картинной плоскости проводится через каждую точку объекта. При этом видимыми будут те точки, которые вдоль направления проектирования ближе всего расположены к картинной плоскости. Задача удаления невидимых линий при ортогональной проекции значительно упрощается, чем при центральном проецировании. Дело в том, что при удалении невидимых линий при центральном проецировании необходимо определять координаты точек пересечения граней объекта с лучами, исходящими из точки наблюдения. Поэтому значительная часть алгоритмов ориентирована на ортогональное проецирование. Если же необходимо применить алгоритм удаления невидимых линий, использующий ортогональное проецирование, а изображение получит в центральной проекции, то сначала надо преобразовать исходную форму объектов в ту форму, которую они получили бы после центрального проецирования.

Алгоритмы удаления невидимых линий или поверхностей можно классифицировать по способу выбора системы координат или пространства, в котором они работают. Алгоритмы удаления невидимых поверхностей условно подразделяют на три большие группы:

· алгоритмы, оперирующие в объектном пространстве;

· алгоритмы, оперирующие в пространстве изображений.

· смешанные алгоритмы.

(Алгоритм отсечение нелицевых граней)

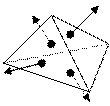Этот метод работает в пространстве объекта и используется для выпуклых многоугольников. Он основан на определении угла 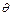между нормаль грани 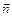и вектором 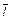, задающим направление проектирования. В зависимости от значения этого угла грани разделяются на лицевые, которые видны и изображаются, и на нелицевые, которые не видны и не изображаются.

Рассмотрим выпуклый многогранник. Для каждой грани построим вектор внешней нормали. Если вектор нормали грани составляет с вектором проектирования тупой угол (90 £q £ 270), то эта грань не видима и она называется нелицевой. Если q является острым (0 < q < 90 или 270 < q < 360), то грань видима и называется 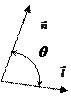лицевой. Таким образом, если cos q > 0, то грань лицевая, а если cos q £ 0, то грань нелицевая.

Вычисления существенно упрощаются, если точку зрения выбрать на оси Z, т.е. направление проектирования будет перпендикулярно плоскости XOY, то видимость плоскостей можно определить при помощи координаты Z их нормалей. Если координата Z нормали > 0, то грань видима, а если координата Z нормали £ 0, то грань невидима.

Пронумеруем все видимые вершины выпуклого многоугольника против часовой стрелки, а невидимые - по ходу часовой стрелки. Для определения координата Z нормали достаточно 3-х вершин

Найдем: dX1=X2-X1; dY1=Y2-Y1; dX2=X3-X2; dY2=Y3-Y2;

Вычислим Z=dX1* dY2 - dX2* dY1

Если Z > 0, то грань видима. Если Z £0, то грань невидима.

Дата добавления: 2014-12-08