Алгоритм плавающего горизонта

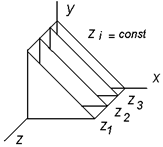Алгоритм плавающего горизонта используется для удаления невидимых линий трехмерного представления функций, описывающих поверхность вида 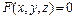. Подобные функции используются математике, технике и др.

Это алгоритм работает в пространстве изображения. Главная идея данного метода заключается в сведении 3-х мерной задачи к двумерной. Это достигается путем пересечения исходной поверхности последовательностью параллельных секущих плоскостей, имеющих постоянные значения координат X, Y или Z. Поверхность теперь складывается из последовательности кривых, лежащих в каждой из этих плоскостей. Чаще всего используются секущие плоскости с постоянной координатой z. При этом функция 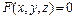сводится последовательности кривых или 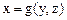, где z постоянно на каждой из заданных параллельных плоскостей. Если спроектировать полученные кривые на плоскость Z=0, как показано на рисунке, то становится ясной идея удаления невидимых участков исходной поверхности. Алгоритм сначала упорядочивает плоскости z=const, по возрастанию расстояния до них от точки наблюдения. Затем для каждой плоскости, начиная с ближайшей к точке наблюдения, строится кривая, лежащая на ней, т.е. для каждого значения координаты х в пространстве изображения определяется соответствующее значение у. Если на текущей плоскости при некотором заданном значении х соответствующее значение у на кривой больше значения у для всех предыдущих кривых при этом значении х, то текущая кривая видима в этой точке, а в противном случае она не видна. Реализация данного алгоритма достаточно проста. Для хранения максимальных значений Y при каждом значении Х используется массив, длина которого равна числу различных точек по оси Х в пространстве изображения. Значения, хранящиеся в этом массиве, представляют собой текущие значения «горизонта». Поэтому по мере рисования каждой очередной кривой этот горизонт «всплывает». Фактически этот алгоритм удаления невидимых линий работает каждый раз с одной линией.

Алгоритм работает хорошо до тех пор, пока какая-нибудь очередная кривая не окажется ниже самой первой из кривых. Подобные кривые, естественно, видимы и представляют собой нижнюю сторону исходной поверхности, однако алгоритм будет считать их невидимыми. Для устранения этого надостатка можно ввести нижний горизонт, который опускается вниз по ходу работы алгоритма. Это реализуется при помощи второго массива, который содержит наименьшее значение у для каждого значения х.

Таким образом, алгоритм будет таким. Если на текущей плоскости при некотором заданном значении х соответствующее значение у на кривой больше максимального или меньше минимального значения у для всех предыдущих кривых при этом значении х, то текущая кривая видима в этой точке, а в противном случае она не видна. Обобщив этот алгоритм, можно рисовать функции, используя полигональную сетку.

3-х мерные изображений

Для построению 3-х мерных изображений на двумерном экране этого попытаемся формализовать рассмотренные ранее элементы, используемые при изображении объемных предметов.

С этой целью введем некоторую произвольную систему координат, в которой точка объекта задается проекциями на некоторую тройку осей в пространстве. Эту систему назовем абсолютной системой.

В этой системе координат будем рассматривать три основные положения предмета:

Исходное;

Фактическое;

Наблюдаемое.

Исходное положение.

Положение объекта, в котором он определяется, называется исходным.

Большая часть изображений объекта состоит из относительно простых предметов, определенным образом расположенных в пространстве. Обычно информация о предмете включает: координаты вершин предмета (координаты (x, y, z)); информация о линиях, соединяющие вершины; информация о видимых поверхностях, которые часто являются плоскими многоугольниками, ограниченными линиями.

Фактическое положение. Положение объекта, в котором он находится в данный момент времени, называется фактическим. Для перевода объекта из исходного в фактическое положение будем использовать матричные вычисления в системе абсолютных координат.

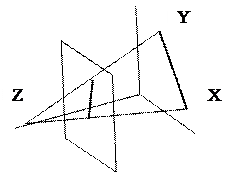Наблюдаемое положение. Понятие наблюдения предполагает, прежде всего, наличие наблюдателя, находящегося в некоторой точке относительно абсолютной системы координат. Наблюдатель смотрит в направлении, задаваемом некоторой точкой. Эта точка определяет направление взгляда. Наблюдаемым положением называется воспринимаемое глазом изображение объекта, получаемое проектированием вершин, линий и поверхностей на двумерную плоскость (визуальную плоскость), расположенную перпендикулярно линии взгляда.

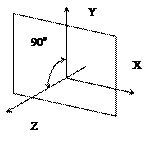
Чаще всего наблюдатель располагается на оси Z, и взгляд направлен вдоль этой оси. Когда все точки пространства переведены в наблюдаемое положение, то визуальной плоскостью является плоскость, параллельная плоскости X/Y (плоскость экрана). Для простоты будем выбирать в качестве визуальной плоскости плоскость, проходящую через начало координат (z=0).

Изображение объектов на визуальной плоскости связано с еще одной геометрической операцией – проецированием при помощи пучка прямых.

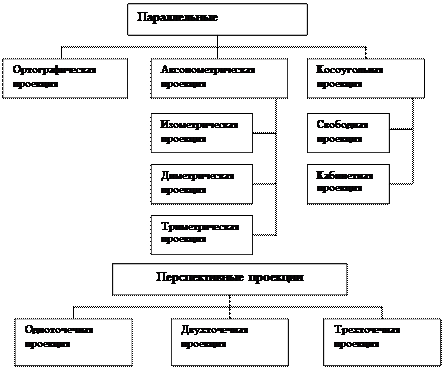
Виды проецирования

В КГ используется несколько различных видов проектирования. Наиболее часто используются два вида проектирования:

· параллельное;

· центральное.

Они различаются по типу используемых проектируемых пучков (собственного или несобственного). Для собственного пучка все прямые исходят из одной точки – центра. Для несобственного пучка центр считается лежащими в бесконечности.

В случае центрального проектирования используется собственный пучок, а при параллельном – несобственный пучок.

Каждый вид проектирования разбивается на несколько подвидов в зависимости от взаимного расположения визуальной плоскости и координатных осей.

Для описаний преобразований, выполняемых при проектировании, используются однородные системы координат (матрицы 4-го порядка). Такое представление преобразований в ряде случаев упрощает решение задач геометрического моделирования.

Виды проекций

Дата добавления: 2014-12-08