Производство работы. Полезная работа. Максимальная работа. Максимальная полезная работа

ЛЕКЦИЯ 7

Если рабочее тело находится в состоянии, отличном от того, которое оно имеет при параметрах окружающей среды (т.е. система не находится в равновесии), то в принципе это раб. тело может произвести работу.

Теперь выясним, как же определить работоспособность системы (работоспособность рабочего тела по отношению к окружающей среде). Итак, изолированная система может произвести работу только в том случае, когда она не находится в равновесном состоянии. Чтобы изолированная система, единственным видом работы которой может быть работа расширения, могла произвести работу, необходимо, чтобы давления или температуры различных тел, входящих в эту систему, не были абсолютно одинаковы.

В системе, состоящей из тел с различными давлениями, отсутствует механическое равновесие. Если в системе имеются тела с различными температурами, в ней отсутствует термическое (тепловое равновесие).

По мере производства работы, изолированная система будет приближаться к равновес- ному состоянию. Допустим, что изолированная система состоит из окр. среды, температура и давление которой практически остаются неизменными, и сжатого воздуха, имеющего ту же температуру, что и окр. среда, но более высокое давление, т.е. налицо механически неравновесное и термически равновесное состояния. Подобная система может производить работу, например, перемещая поршень в цилиндре до тех пор, пока давление воздуха не снизится до давления окр. среды, т.е. пока система не придет в механическое равновесие.

Если в системе имеются два источника теплоты, обладающих различными температурами, и раб. тело, начальное состояние которого значения не имеет, то мы имеем дело с термодинамической равновесной системой, которая может произвести работу, например, путем неоднократного повторения рабочим телом цикла Карно. В результате совершения цикла Карно не только оказывается произведенной известная работа, но также вполне определенное количество теплоты передается от источника с более высокой температурой к источнику с более низкой. Но в результате такого перехода теплоты, температура горячего источника будет понижаться, а холодного – повышаться. С течением времени температуры источников теплоты сделаются одинаковым, система достигнет термодинамического равновесия, и дальнейшее производство работы станет невозможным.

Таким образом, производство работы изолированной системой возможно только в процессе перехода системы из неравновесного состояния в равновесное. Произведенная работа зависит, как известно, от характера процесса перехода системы к равновесному состоянию.

Допустим снова, что в нашем распоряжении имеется термически неравновесная система, состоящая из двух источников теплоты, имеющих различные температуры и раб. тела. Теплота передается непосредственно от горячего источника к холодному, минуя раб. тело. В результате такого процесса, температуры всех тел системы станут одинаковыми, система окажется в состоянии термического равновесия, а никакой работы вообще не будет произведено. Подобный процесс теплообмена, (приводящий к выравниванию температур) без производства работы обязательно должен происходить при конечной разности температур, т.е. необратимо.

Наоборот, максимальная работа при переходе системы от термически неравновесного состояния в равновесное может быть получено в результате неоднократного совершения раб. телом цикла Карно, в котором наибольшая температура раб. тела равна температуре горячего источника, а наименьшая температура – температуре холодного источника, т.е. в

результате совершения только полностью обратимых процессов.

Если изолированная система механически неравновесна, то в этом случае наибольшая работа, которую можно получить при переходе из механически неравновесного состояния в равновесное, может быть получена в результате осуществления полностью обратимых процессов. Ясно, что наибольшая работа будет получена в случае отсутствия трения между поршнем и стенками цилиндра машины. Но трение представляет собой типичный необратимый процесс.

Таким образом, мы пришли к двум очень важным выводам:

1. Изолированная система способна к производству работы только в случае,когда

она находится в неравновесном состоянии. После достижения равновесного состояния работоспособность системы оказывается исчерпанной.

2. Для получения наибольшей возможной работы при переходе системы из

неравновесного состояния в равновесное, нужно, чтобы все процессы, протекающие в системе были полностью обратимы.

Определим теперь более четко понятия полезной работы, максимальной работы и мак- симально-полезной работы, которая может быть произведена рассматриваемой системой.

Попробуем численно определить максимальную полезную работу, которую может произ- вести система, или, как иногда говорят, определим работоспособность системы. В нашем распоряжении имеется изолированная система, состоящая из окруж. среды и некоторого тела

имеющих отличные от среды давление р и температуру Т (или один из этих параметров).

Такое тело или группу тел будем наз. в дальнейшем источником работы.

В неравновесной изолированной системе работа производится при изменении состояния источника работы в процессе установления равновесия в этой системе. Обозначим эту работу L. Часть этой работы будет затрачиваться на сжатие окр. среды. Т.к. система изолирована, то ее объем явл. постоянным, поэтому увеличение его на величину 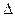V в процессе установления равновесия в системе может происходить только за счет уменьшения на ту же величину 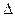V объема окружающей среды.

Работу, затраченную на сжатие окр. среды (против сил давления среды), обозначим L₀.

Поскольку часть работы, производимой в процессе установления равновесия в изолированной системе, всегда будет затрачиваться на сжатие окр. среды, то, следовательно, использовать по своему усмотрению мы можем не всю произведенную работу L, а только ту ее часть, которая остается за вычетом L₀. Эту часть произведенной работы условимся наз. полезной работой. L_пол.=L – L₀, (7.1)

Как уже отмечалось, если переход системы из неравновесного состояния в равновесное осуществляется при помощи обратимых процессов, то в этом случай система произведет наибольшую возможную в данных условиях работу (т.е. произведенная работа будет максимальной). Т.к. все реальные процессы явлю в большей или в меньшей степени необратимыми, то максимальная работа системы явл. недостижимым пределом. Однако для сравнения степени совершенства процессов получения работы понятие о подобном пределе оказывается полезным. Максимальную работу системы обозначим L^макс.. Максимальная полезная работа – 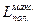, которую может произвести система (работоспособность системы) – это, по аналогии с уравнением (7.1), часть максимальной работы, за вычетом работы, затрачиваемой на сжатие окр. среды: 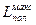=L^макс. – L_0, (7.2)

Определим 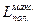. Допустим, что температура Т₀ и давление р₀ окр. среды неизменны. Начальные параметры источника работы: p, V, T, U, S, h. работы: p_к, V_к, T_к, U_к, S_к, Н_к. Конечные параметры окр. среды: p_0к, V_0к, T_0к, U_0к, S_0к, Н_0к. Причем р_к=р₀ и Т_к=Т₀.

Суммарная внутренняя энергия системы в начальном, неравновесном состоянии:

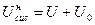, (7.3)

Суммарная внутренняя энергия системы в конечном равновесном состоянии

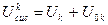, (7.4)

Т.к. рассматриваемая система по определению явл. изолированной (бq_сис.=0), то из уравнения 1-го закона ТТД следует, что работа может быть произведена системой только за счет уменьшения ее внутр. єнергии: 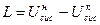, (7.5)

С учетом (7.3) и (7.4) получаем: L=(U+U₀) – (U_k+U_0k)=(U – U_k)+(U₀ – U_0k), (7.6)

Но между источником работы и окружающей средой может существовать теплообмен, кроме того, источник работы может совершать работу над средой (против давления среды). Обозначим Q₂ теплоту, переданную источником работы среде, а L₀ – работу, совершенную источником работы над средой. В соответствии с 1-ым законом ТТД:

U_оk – U_о=Q₂+L_о, (7.7)

Т.к. давление среды р₀ по условию неизменно, то: L_о=p_о(V_к – V), (7.8)

Поскольку рассматриваемая система явл. Изолированной, ее суммарный объем постоянен и, следовательно, изменение объема одной части этой системы-среды равно по величине (и противоположно по знаку) изменению объема другой ее части – источника работы. Поэтому в уравнении (7.8) для L₀ – работа сжатия окружающей среды – фигурирует изменение объема источника работы V_к – V, а не окружающей среды V₀ – V_к.

Тогда, меняя знак в (7.7) и подставляя L₀ из (7.8), получим:

U₀ – U_0к= - Q₂ – p₀(V_к – V), (7.9)

Подставляя значение U₀ – U_0к из уравнения (7.9) в (7.6), получаем:

L=(U – U_к) – Q₂ – p₀(V_к – V), (7.10)

Теплота, переданная от источника работы окружающей среде, равна, очевидно, произведению неизменной температуры среды Т₀ и приращению энтропии среды (S_0к – S₀), т.е. Q₂=T₀(S_0k – S₀), (7.11)

Подставляя значение Q₂ из уравнения (7.11) в уравнение (7.10), получаем:

L=(U – U_к) – Т₀(S_0k – S₀) – p₀(V_к – V), (7.12)

Уравнение (7.12) дает значение полезной работы.

Для того, чтобы найти максимальную полезную работу (работоспособность) изолированной системы, необходимо воспользоваться положением о том, что в результате протекания обратимых процессов энтропия изолированной системы не изменяется. Отсюда следует, с учетом аддитивности энтропии, что если энтропия источника работы уменьшалась на S – S_к, то энтропия среды должна возрасти на то же значение, т.е. для обратимых процессов: S_0к – S₀=S – S_к, (7.13)

Подставляя (7.13) в (7.12) получим выражение для максимальной полезной работы изолированной системы: 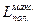=(U – U_к) – T₀(S – S_к) – p₀(V_к – V), (7.14)

Как видно из (7.14), максимальная полезная работа системы однозначно определяется начальными параметрами источника работы и параметрами окр. среды.

Дата добавления: 2014-11-29